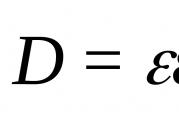นักเรียนมัธยมปลายและนักเรียนที่เชี่ยวชาญด้านคณิตศาสตร์มักจะตอบคำถามนี้ได้อย่างง่ายดาย แต่สำหรับผู้ที่อยู่ห่างไกลจากอาชีพนี้จะยากขึ้น มันคืออะไรจริงๆ?

สาระสำคัญและการกำหนด

จำนวนตรรกยะคือจำนวนที่สามารถแสดงในรูปแบบ เศษส่วนร่วม. บวกลบรวมทั้งศูนย์รวมอยู่ในชุดนี้ด้วย ตัวเศษของเศษส่วนต้องเป็นจำนวนเต็ม และตัวส่วนต้องเป็น

เซตนี้เขียนแทนด้วยคณิตศาสตร์ว่า Q และเรียกว่า "ฟิลด์ สรุปตัวเลข" มันรวมถึงจำนวนเต็มและจำนวนธรรมชาติทั้งหมดซึ่งแสดงตามลำดับเป็น Z และ N ชุด Q นั้นรวมอยู่ในชุด R มันคือตัวอักษรนี้ที่แสดงถึงสิ่งที่เรียกว่าจริงหรือ

ผลงาน

ตามที่กล่าวไว้แล้ว จำนวนตรรกยะคือชุดที่รวมค่าจำนวนเต็มและค่าเศษส่วนทั้งหมด สามารถนำเสนอได้ใน รูปแบบที่แตกต่างกัน. อย่างแรก ในรูปของเศษส่วนธรรมดา: 5/7, 1/5, 11/15 เป็นต้น แน่นอนว่าจำนวนเต็มสามารถเขียนในรูปแบบที่คล้ายกันได้: 6/2, 15/5, 0/1, - 10/2 เป็นต้น ประการที่สอง การแทนค่าอีกประเภทหนึ่งคือ ทศนิยมด้วยเศษส่วนสุดท้าย: 0.01, -15.001006 เป็นต้น นี่อาจเป็นหนึ่งในรูปแบบที่พบได้บ่อยที่สุด

แต่ยังมีหนึ่งในสาม - เศษส่วนเป็นระยะ ประเภทนี้ไม่ค่อยพบบ่อย แต่ก็ยังใช้อยู่ ตัวอย่างเช่น เศษส่วน 10/3 สามารถเขียนเป็น 3.33333... หรือ 3,(3) ในกรณีนี้ การเป็นตัวแทนที่แตกต่างกันจะถือเป็นตัวเลขที่คล้ายกัน เศษส่วนที่เท่ากันจะเรียกว่า 3/5 และ 6/10 ดูเหมือนว่าจะชัดเจนว่าจำนวนตรรกยะคืออะไร แต่ทำไมคำนี้ถึงใช้เรียกพวกเขา?

ที่มาของชื่อ

คำว่า "มีเหตุผล" ในภาษารัสเซียสมัยใหม่มักมีความหมายแตกต่างกันเล็กน้อย มันค่อนข้าง "สมเหตุสมผล" "พิจารณา" แต่คำศัพท์ทางคณิตศาสตร์ใกล้เคียงกับความหมายโดยตรงของสิ่งนี้ ในภาษาละติน "อัตราส่วน" คือ "อัตราส่วน" "เศษส่วน" หรือ "การหาร" ดังนั้น ชื่อจึงสะท้อนถึงสาระสำคัญของจำนวนตรรกยะ อย่างไรก็ตามความหมายที่สอง

ไม่ไกลจากความจริง

การดำเนินการกับพวกเขา

เมื่อแก้ปัญหาทางคณิตศาสตร์ เราพบจำนวนตรรกยะตลอดเวลาโดยที่เราไม่รู้ตัว และมีคุณสมบัติที่น่าสนใจมากมาย ทั้งหมดเป็นไปตามนิยามของชุดหรือจากการกระทำ

ประการแรก จำนวนตรรกยะมีคุณสมบัติความสัมพันธ์ของลำดับ ซึ่งหมายความว่ามีเพียงอัตราส่วนเดียวเท่านั้นที่สามารถมีอยู่ระหว่างตัวเลขสองตัว - อัตราส่วนทั้งสองมีค่าเท่ากันหรือมีค่ามากกว่าหรือน้อยกว่าอีกค่าหนึ่ง เช่น.:

หรือ เอ = บีหรือ ก > ขหรือ ก< b.

นอกจากนี้ คุณสมบัตินี้ยังแสดงถึงการเปลี่ยนแปลงของความสัมพันธ์ นั่นคือถ้า กมากกว่า ข, ขมากกว่า ค, ที่ กมากกว่า ค. ในภาษาคณิตศาสตร์ มีลักษณะดังนี้

(ก > ข) ^ (ข > ค) => (ก > ค).

ประการที่สอง มีการดำเนินการทางคณิตศาสตร์ด้วยจำนวนตรรกยะ นั่นคือ การบวก การลบ การหาร และการคูณ ในเวลาเดียวกัน คุณสมบัติหลายอย่างสามารถแยกแยะได้ในกระบวนการของการเปลี่ยนแปลง

• a + b = b + a (การแทนที่ของเงื่อนไข, การสลับที่);
• 0 + ก = ก + 0 ;
• (a + b) + c = a + (b + c) (การเชื่อมโยง);
• ก + (-ก) = 0;
• ab = บา;
• (ab)c = a(bc) (การกระจาย);
• ก x 1 = 1 x ก = ก;
• a x (1 / a) = 1 (ในกรณีนี้ a ไม่เท่ากับ 0);
• (a + b)ค = แอค + ab;
• (ก > ข) ^ (ค > 0) => (ac > bc).

เมื่อพูดถึงเรื่องปกติและไม่ใช่หรือจำนวนเต็ม การดำเนินการกับพวกมันอาจทำให้เกิดปัญหาบางอย่างได้ ดังนั้น การบวกและการลบจะทำได้ก็ต่อเมื่อตัวส่วนเท่ากันเท่านั้น หากพวกมันต่างกันตั้งแต่แรก คุณควรหาตัวหารร่วมโดยใช้การคูณเศษส่วนทั้งหมดด้วยตัวเลขที่แน่นอน การเปรียบเทียบมักจะเป็นไปได้ก็ต่อเมื่อตรงตามเงื่อนไขนี้เท่านั้น

การหารและการคูณเศษส่วนสามัญจะดำเนินการอย่างเพียงพอ กฎง่ายๆ. ไม่จำเป็นต้องลดให้เหลือส่วนร่วม ตัวเศษและตัวส่วนจะถูกคูณแยกกันในขณะที่อยู่ในขั้นตอนของการดำเนินการ ถ้าเป็นไปได้ เศษส่วนควรลดลงและทำให้ง่ายขึ้นมากที่สุด

สำหรับการหาร การกระทำนี้คล้ายกับครั้งแรกโดยมีความแตกต่างกันเล็กน้อย สำหรับเศษส่วนที่สอง คุณควรหาส่วนกลับ นั่นคือ

"กลับมัน. ดังนั้น ตัวเศษของเศษส่วนแรกจะต้องคูณด้วยตัวส่วนของส่วนที่สองและในทางกลับกัน

สุดท้าย คุณสมบัติอื่นที่มีอยู่ในจำนวนตรรกยะเรียกว่าสัจพจน์ของอาร์คิมิดีส คำว่า "หลักการ" มักพบในวรรณคดีเช่นกัน ใช้ได้กับจำนวนจริงทั้งชุด แต่ไม่ใช่ทุกที่ ดังนั้น หลักการนี้ใช้ไม่ได้กับฟังก์ชันตรรกยะบางชุด โดยพื้นฐานแล้ว สัจพจน์นี้หมายความว่า เนื่องจากการมีอยู่ของปริมาณ a และ b สองปริมาณ คุณจึงสามารถนำ a เกิน b ได้เสมอ

พื้นที่ใช้งาน

ดังนั้น สำหรับผู้ที่เรียนรู้หรือจำได้ว่าจำนวนตรรกยะคืออะไร จะเห็นได้ชัดว่ามีการใช้ตัวเลขเหล่านี้ทุกที่: ในบัญชี เศรษฐศาสตร์ สถิติ ฟิสิกส์ เคมี และวิทยาศาสตร์อื่นๆ โดยธรรมชาติแล้วพวกเขามีสถานที่ในวิชาคณิตศาสตร์ด้วย ไม่ทราบว่าเรากำลังติดต่อกับพวกเขาอยู่เสมอเราใช้จำนวนตรรกยะอย่างต่อเนื่อง แม้แต่เด็กเล็กที่เรียนรู้ที่จะนับสิ่งของ หั่นแอปเปิ้ลเป็นชิ้นๆ หรือทำท่าทางง่ายๆ พวกเขาล้อมรอบเราอย่างแท้จริง และยังไม่เพียงพอสำหรับการแก้ปัญหาบางอย่าง โดยเฉพาะอย่างยิ่ง การใช้ทฤษฎีบทพีทาโกรัสเป็นตัวอย่าง เราสามารถเข้าใจความจำเป็นในการแนะนำแนวคิด

หัวข้อของจำนวนตรรกยะค่อนข้างกว้างขวาง คุณสามารถพูดคุยเกี่ยวกับมันได้ไม่รู้จบและเขียนงานทั้งหมดทุกครั้งที่ชิปใหม่ประหลาดใจ

เพื่อหลีกเลี่ยงข้อผิดพลาดในอนาคต ในบทนี้เราจะเจาะลึกหัวข้อจำนวนตรรกยะเล็กน้อย ดึงข้อมูลที่จำเป็นจากนั้นไปต่อ

เนื้อหาบทเรียน

จำนวนตรรกยะคืออะไร

จำนวนตรรกยะคือจำนวนที่สามารถแสดงเป็นเศษส่วน โดยที่ เอ -เป็นตัวเศษของเศษส่วน ขเป็นตัวส่วนของเศษส่วน และ ขต้องไม่เป็นศูนย์ เนื่องจากไม่อนุญาตให้หารด้วยศูนย์

จำนวนตรรกยะรวมถึงหมวดหมู่ของตัวเลขต่อไปนี้:

• จำนวนเต็ม (เช่น -2, -1, 0 1, 2 เป็นต้น)

• เศษส่วนทศนิยม (เช่น 0.2 เป็นต้น)

• เศษส่วนเป็นระยะไม่สิ้นสุด (เช่น 0, (3) เป็นต้น)

ตัวเลขแต่ละตัวในหมวดนี้สามารถแสดงเป็นเศษส่วนได้

ตัวอย่างที่ 1จำนวนเต็ม 2 สามารถแสดงเป็นเศษส่วนได้ ดังนั้น เลข 2 จึงไม่ใช้กับจำนวนเต็มเท่านั้น แต่ยังใช้กับจำนวนตรรกยะด้วย

ตัวอย่างที่ 2จำนวนคละสามารถแสดงเป็นเศษส่วนได้ เศษส่วนนี้ได้มาจากการแปลงจำนวนคละให้เป็นเศษเกิน

จำนวนคละจึงเป็นจำนวนตรรกยะ

ตัวอย่างที่ 3ทศนิยม 0.2 สามารถแสดงเป็นเศษส่วนได้ เศษส่วนนี้ได้มาจากการแปลงเศษส่วนทศนิยม 0.2 เป็นเศษส่วนสามัญ หากคุณประสบปัญหาในจุดนี้ ให้ทำซ้ำหัวข้อนี้

เนื่องจากเศษส่วนทศนิยม 0.2 สามารถแสดงเป็นเศษส่วนได้ หมายความว่ามันใช้กับจำนวนตรรกยะด้วย

ตัวอย่างที่ 4เศษส่วนเป็นระยะอนันต์ 0, (3) สามารถแสดงเป็นเศษส่วนได้ เศษส่วนนี้ได้มาจากการแปลงเศษส่วนบริสุทธิ์เป็นเศษส่วนธรรมดา หากคุณประสบปัญหาในจุดนี้ ให้ทำซ้ำหัวข้อนี้

เนื่องจากเศษส่วนเป็นระยะอนันต์ 0, (3) สามารถแสดงเป็นเศษส่วนได้ หมายความว่าเศษส่วนนั้นเป็นของจำนวนตรรกยะด้วย

ในอนาคต ตัวเลขทั้งหมดที่สามารถแสดงเป็นเศษส่วนได้ เราจะเรียกหนึ่งวลีมากขึ้นเรื่อยๆ - สรุปตัวเลข.

จำนวนตรรกยะบนเส้นพิกัด

เราพิจารณาเส้นพิกัดเมื่อเราศึกษาจำนวนลบ จำไว้ว่านี่คือเส้นตรงที่มีหลายจุดอยู่ ดังต่อไปนี้:

รูปนี้แสดงส่วนเล็ก ๆ ของเส้นพิกัดตั้งแต่ −5 ถึง 5

การทำเครื่องหมายจำนวนเต็มในรูปแบบ 2, 0, −3 บนเส้นพิกัดไม่ใช่เรื่องยาก

มาก สิ่งที่น่าสนใจมากขึ้นสถานการณ์เป็นตัวเลขที่เหลือ: ด้วยเศษส่วนธรรมดา ตัวเลขผสม เศษส่วนทศนิยม ฯลฯ ตัวเลขเหล่านี้อยู่ระหว่างจำนวนเต็มและมีจำนวนมากมายนับไม่ถ้วน

ตัวอย่างเช่น ลองทำเครื่องหมายจำนวนตรรกยะบนเส้นพิกัด ตัวเลขนี้อยู่ระหว่างศูนย์ถึงหนึ่ง

ลองทำความเข้าใจว่าทำไมเศษส่วนจึงอยู่ระหว่างศูนย์ถึงหนึ่ง

ดังที่กล่าวไว้ข้างต้น ระหว่างจำนวนเต็มคือตัวเลขอื่นๆ เช่น เศษส่วนธรรมดา เศษส่วนทศนิยม ตัวเลขผสม เป็นต้น ตัวอย่างเช่น หากคุณเพิ่มส่วนของเส้นพิกัดจาก 0 เป็น 1 คุณจะเห็นรูปภาพต่อไปนี้

จะเห็นได้ว่าระหว่างจำนวนเต็ม 0 และ 1 มีจำนวนตรรกยะอื่น ๆ ซึ่งเป็นเศษส่วนทศนิยมที่เราคุ้นเคยอยู่แล้ว เศษส่วนของเรายังปรากฏที่นี่ ซึ่งอยู่ในตำแหน่งเดียวกับเศษส่วนทศนิยม 0.5 การตรวจสอบตัวเลขนี้อย่างละเอียดจะให้คำตอบสำหรับคำถามที่ว่าทำไมเศษส่วนถึงอยู่ที่นั่น

เศษส่วนหมายถึงการหาร 1 ด้วย 2 และถ้าเราหาร 1 ด้วย 2 เราจะได้ 0.5

เศษส่วนทศนิยม 0.5 สามารถปลอมเป็นเศษส่วนอื่นได้ จากคุณสมบัติพื้นฐานของเศษส่วน เรารู้ว่าหากตัวเศษและตัวส่วนของเศษส่วนคูณหรือหารด้วยจำนวนเดียวกัน ค่าของเศษส่วนจะไม่เปลี่ยนแปลง

หากตัวเศษและตัวส่วนของเศษส่วนคูณด้วยจำนวนใดๆ เช่น เลข 4 เราจะได้เศษส่วนใหม่ และเศษส่วนนี้ก็เท่ากับ 0.5 ด้วย

ซึ่งหมายความว่าบนเส้นพิกัด เศษส่วนสามารถวางในตำแหน่งเดียวกับที่เศษส่วนนั้นอยู่ได้

ตัวอย่างที่ 2มาลองทำเครื่องหมายจำนวนตรรกยะบนพิกัดกัน หมายเลขนี้อยู่ระหว่างหมายเลข 1 และ 2

ค่าของเศษส่วนคือ 1.5

ถ้าเราเพิ่มส่วนของเส้นพิกัดจาก 1 เป็น 2 เราจะเห็นภาพต่อไปนี้:

จะเห็นได้ว่าระหว่างจำนวนเต็ม 1 และ 2 มีจำนวนตรรกยะอื่น ๆ ซึ่งเป็นเศษส่วนทศนิยมที่เราคุ้นเคยอยู่แล้ว เศษส่วนของเรายังปรากฏที่นี่ ซึ่งอยู่ในตำแหน่งเดียวกับเศษส่วนทศนิยม 1.5

เราเพิ่มบางส่วนบนเส้นพิกัดเพื่อดูตัวเลขที่เหลือที่อยู่ในส่วนนี้ เป็นผลให้เราพบเศษส่วนทศนิยมที่มีหนึ่งหลักหลังจุดทศนิยม

แต่นี่ไม่ใช่ตัวเลขเดียวที่อยู่ในกลุ่มเหล่านี้ มีตัวเลขมากมายนับไม่ถ้วนอยู่บนเส้นพิกัด

เดาได้ง่ายว่าระหว่างเศษส่วนทศนิยมที่มีเลขหลังจุดทศนิยมหนึ่งหลัก มีเศษส่วนทศนิยมอื่นๆ ที่มีเลขหลังจุดทศนิยมสองหลักอยู่แล้ว กล่าวอีกนัยหนึ่งคือหนึ่งในร้อยของส่วน

เช่น ลองดูตัวเลขที่อยู่ระหว่างเศษส่วนทศนิยม 0.1 ถึง 0.2

ตัวอย่างอื่น. ทศนิยมที่มีตัวเลขสองหลักหลังจุดทศนิยมและอยู่ระหว่างศูนย์กับจำนวนตรรกยะ 0.1 มีลักษณะดังนี้:

ตัวอย่างที่ 3เราทำเครื่องหมายจำนวนตรรกยะบนเส้นพิกัด จำนวนตรรกยะนี้จะเข้าใกล้ศูนย์มาก

ค่าของเศษส่วนคือ 0.02

หากเราเพิ่มส่วนจาก 0 เป็น 0.1 เราจะดูว่าจำนวนตรรกยะอยู่ที่ตำแหน่งใด

จะเห็นได้ว่าจำนวนตรรกยะของเราอยู่ที่ตำแหน่งเดียวกับเศษส่วนทศนิยม 0.02

ตัวอย่างที่ 4ให้เราทำเครื่องหมายจำนวนตรรกยะ 0 บนเส้นพิกัด (3)

จำนวนตรรกยะ 0, (3) เป็นเศษส่วนเป็นระยะที่ไม่สิ้นสุด เศษส่วนของมันไม่สิ้นสุด มันเป็นอนันต์

และเนื่องจากเลข 0, (3) มีส่วนที่เป็นเศษส่วนไม่สิ้นสุด หมายความว่าเราจะไม่สามารถหาตำแหน่งที่แน่นอนบนเส้นพิกัดที่ตัวเลขนี้ตั้งอยู่ได้ เราสามารถระบุสถานที่นี้โดยประมาณเท่านั้น

จำนวนตรรกยะ 0.33333… จะใกล้เคียงกับทศนิยมปกติ 0.3 มาก

ตัวเลขนี้ไม่ได้แสดงตำแหน่งที่แน่นอนของเลข 0,(3) นี่เป็นเพียงภาพประกอบที่แสดงให้เห็นว่าเศษส่วนคาบ 0.(3) สามารถเข้าใกล้ทศนิยมปกติ 0.3 ได้อย่างไร

ตัวอย่างที่ 5เราทำเครื่องหมายจำนวนตรรกยะบนเส้นพิกัด จำนวนตรรกยะนี้จะอยู่ตรงกลางระหว่างเลข 2 และ 3

นี่คือ 2 (จำนวนเต็มสองจำนวน) และ (หนึ่งวินาที) เศษส่วนเรียกอีกอย่างว่า "ครึ่ง" ดังนั้นเราจึงทำเครื่องหมายสองส่วนทั้งหมดและอีกครึ่งหนึ่งของส่วนบนเส้นพิกัด

ถ้าเราแปลงจำนวนคละเป็นเศษเกิน เราจะได้เศษส่วนธรรมดา เศษส่วนนี้บนเส้นพิกัดจะอยู่ที่เดียวกับเศษส่วน

ค่าของเศษส่วนคือ 2.5

ถ้าเราเพิ่มส่วนของเส้นพิกัดจาก 2 เป็น 3 เราจะเห็นภาพต่อไปนี้:

จะเห็นได้ว่าจำนวนตรรกยะของเราอยู่ที่ตำแหน่งเดียวกับเศษส่วนทศนิยม 2.5

ลบก่อนจำนวนตรรกยะ

ในบทเรียนก่อนหน้านี้ที่เรียกว่า เราได้เรียนรู้วิธีการหารจำนวนเต็ม เงินปันผลและตัวหารสามารถเป็นได้ทั้งจำนวนบวกและลบ

พิจารณานิพจน์ที่ง่ายที่สุด

(−6) : 2 = −3

ในนิพจน์นี้ เงินปันผล (−6) เป็นจำนวนลบ

พิจารณานิพจน์ที่สอง

6: (−2) = −3

ที่นี่ ตัวหาร (−2) เป็นจำนวนลบแล้ว แต่ในทั้งสองกรณี เราได้คำตอบเดียวกันคือ -3

เนื่องจากการหารใด ๆ สามารถเขียนเป็นเศษส่วน เรายังสามารถเขียนตัวอย่างที่กล่าวถึงข้างต้นเป็นเศษส่วน:

และเนื่องจากในทั้งสองกรณีค่าของเศษส่วนเท่ากัน การลบที่อยู่ในตัวเศษหรือตัวส่วนจึงสามารถทำได้โดยการวางไว้หน้าเศษส่วน

ดังนั้น คุณสามารถใส่เครื่องหมายเท่ากับระหว่างนิพจน์ และ และ เนื่องจากมีค่าเท่ากัน

ในอนาคต การทำงานกับเศษส่วน ถ้าเราพบเครื่องหมายลบในตัวเศษหรือตัวส่วน เราจะทำให้เครื่องหมายลบนี้ร่วมกัน โดยวางไว้หน้าเศษส่วน

ตรงข้ามจำนวนตรรกยะ

เช่นเดียวกับจำนวนเต็ม จำนวนตรรกยะจะมีจำนวนตรงข้าม

ตัวอย่างเช่น สำหรับจำนวนตรรกยะ จำนวนตรงข้ามคือ ตั้งอยู่บนเส้นพิกัดที่สมมาตรกับตำแหน่งที่สัมพันธ์กับจุดกำเนิด กล่าวอีกนัยหนึ่ง ตัวเลขทั้งสองนี้อยู่ห่างจากจุดกำเนิดเท่ากัน

แปลงจำนวนคละเป็นเศษเกิน

เรารู้ว่าในการแปลงจำนวนคละเป็นเศษเกิน คุณต้องคูณส่วนจำนวนเต็มด้วยตัวส่วนของเศษส่วนแล้วบวกเข้ากับตัวเศษของส่วนที่เป็นเศษส่วน ตัวเลขที่ได้จะเป็นตัวเศษของเศษส่วนใหม่ ในขณะที่ตัวส่วนยังคงเหมือนเดิม

ตัวอย่างเช่น ลองแปลงจำนวนคละเป็นเศษเกิน

คูณส่วนจำนวนเต็มด้วยตัวส่วนของเศษส่วนและเพิ่มตัวเศษของส่วนที่เป็นเศษส่วน:

ลองคำนวณนิพจน์นี้:

(2 × 2) + 1 = 4 + 1 = 5

ผลลัพธ์ที่ได้คือ 5 จะเป็นตัวเศษของเศษส่วนใหม่ และตัวส่วนจะยังคงเหมือนเดิม:

กระบวนการทั้งหมดเขียนดังนี้:

หากต้องการคืนค่าจำนวนคละดั้งเดิม ให้เลือกส่วนจำนวนเต็มในเศษส่วนก็เพียงพอแล้ว

แต่วิธีแปลงจำนวนคละเป็นเศษเกินนี้ใช้ได้เฉพาะเมื่อจำนวนคละเป็นบวกเท่านั้น สำหรับจำนวนลบ ทางนี้จะไม่ทำงาน

ลองพิจารณาเศษส่วน ลองนำส่วนจำนวนเต็มของเศษส่วนนี้กัน รับ

หากต้องการคืนค่าเศษส่วนเดิม คุณต้องแปลงจำนวนคละเป็นเศษเกิน แต่ถ้าเราใช้กฎเดิม กล่าวคือ เราคูณส่วนจำนวนเต็มด้วยตัวส่วนของส่วนที่เป็นเศษส่วน แล้วบวกตัวเศษของส่วนที่เป็นเศษส่วนกับจำนวนผลลัพธ์ เราจะได้ความขัดแย้งดังต่อไปนี้:

เราได้เศษส่วน แต่เราควรได้รับเศษส่วน

เราสรุปได้ว่าจำนวนคละถูกแปลงเป็นเศษส่วนที่ไม่ถูกต้อง

ในการแปลจำนวนคละที่เป็นลบให้เป็นเศษส่วนที่ไม่ถูกต้อง คุณต้องคูณส่วนจำนวนเต็มด้วยตัวส่วนของส่วนที่เป็นเศษส่วน และจากจำนวนผลลัพธ์ ลบตัวเศษ ในกรณีนี้ทุกอย่างจะเข้าที่

จำนวนคละที่เป็นลบตรงข้ามกับจำนวนคละ หากจำนวนคละบวกอยู่ทางด้านขวาและมีลักษณะดังนี้

สรุปตัวเลข

ไตรมาส

1. ความเป็นระเบียบ กและ ขมีกฎที่อนุญาตให้คุณระบุระหว่างความสัมพันธ์หนึ่งและหนึ่งในสามความสัมพันธ์โดยไม่ซ้ำกัน: “< », « >' หรือ ' = ' กฎนี้เรียกว่า กฎการสั่งซื้อและมีสูตรดังนี้สอง ตัวเลขติดลบและสัมพันธ์กันด้วยความสัมพันธ์เดียวกันกับจำนวนเต็มสองจำนวน และ ; สองไม่ได้ ตัวเลขที่เป็นบวก กและ ขสัมพันธ์กันด้วยความสัมพันธ์เดียวกันกับตัวเลขที่ไม่เป็นลบสองตัว และ ; ถ้ากระทันหัน กไม่เป็นลบและ ข- ติดลบแล้ว ก > ข. src="/pictures/wiki/files/57/94586b8b651318d46a00db5413cf6c15.png" border="0">

   

   ผลรวมของเศษส่วน

2. การดำเนินการเพิ่มเติมสำหรับจำนวนตรรกยะใดๆ กและ ขมีสิ่งที่เรียกว่า กฎการรวม ค. อย่างไรก็ตามตัวเลขดังกล่าว คเรียกว่า ผลรวมตัวเลข กและ ขและแสดงแทน และกระบวนการค้นหาหมายเลขดังกล่าวเรียกว่า ผลรวม. กฎการรวมมีรูปแบบดังต่อไปนี้: .
3. การดำเนินการคูณสำหรับจำนวนตรรกยะใดๆ กและ ขมีสิ่งที่เรียกว่า กฎการคูณซึ่งทำให้พวกมันสอดคล้องกับจำนวนตรรกยะ ค. อย่างไรก็ตามตัวเลขดังกล่าว คเรียกว่า งานตัวเลข กและ ขและแสดงแทน และกระบวนการค้นหาหมายเลขดังกล่าวก็เรียกเช่นกัน การคูณ. กฎการคูณมีดังนี้: .
4. การเปลี่ยนแปลงของลำดับความสัมพันธ์สำหรับจำนวนตรรกยะใด ๆ ก , ขและ คถ้า กน้อย ขและ ขน้อย ค, ที่ กน้อย ค, และถ้า กเท่ากับ ขและ ขเท่ากับ ค, ที่ กเท่ากับ ค. 6435">การสลับที่ของการบวก ผลรวมไม่เปลี่ยนจากการเปลี่ยนตำแหน่งของเงื่อนไขที่เป็นตรรกยะ
5. ความเชื่อมโยงของการบวกลำดับที่เพิ่มจำนวนตรรกยะสามตัวไม่มีผลกับผลลัพธ์
6. การปรากฏตัวของศูนย์มีเลขตรรกยะ 0 ที่รักษาจำนวนตรรกยะอื่น ๆ ทุกจำนวนเมื่อบวก
7. การปรากฏตัวของจำนวนตรงข้ามจำนวนตรรกยะใดๆ จะมีจำนวนตรรกยะตรงกันข้าม ซึ่งเมื่อรวมแล้วจะได้ 0
8. การสับเปลี่ยนของการคูณผลิตภัณฑ์จะไม่เปลี่ยนแปลงโดยการเปลี่ยนตำแหน่งของปัจจัยที่มีเหตุผล
9. ความสัมพันธ์ของการคูณลำดับที่จำนวนตรรกยะสามตัวถูกคูณจะไม่ส่งผลต่อผลลัพธ์
10. การปรากฏตัวของหน่วยมีจำนวนตรรกยะ 1 ที่รักษาจำนวนตรรกยะอื่น ๆ เมื่อคูณ
11. การปรากฏตัวของซึ่งกันและกันจำนวนตรรกยะใดๆ จะมีจำนวนตรรกยะผกผัน ซึ่งเมื่อคูณแล้วจะได้ 1
12. การกระจายของการคูณเกี่ยวกับการบวกการดำเนินการคูณสอดคล้องกับการดำเนินการบวกผ่านกฎการกระจาย:
13. การเชื่อมโยงความสัมพันธ์ของลำดับกับการดำเนินการของการบวกไปทางซ้ายและขวา ความไม่เท่าเทียมกันเชิงเหตุผลคุณสามารถบวกจำนวนตรรกยะเดียวกันได้ /ภาพ/wiki/files/51/358b88fcdff63378040f8d9ab9ba5048.png" border="0">
14. สัจพจน์ของอาร์คิมิดีสอะไรก็ตามที่เป็นจำนวนตรรกยะ กคุณสามารถใช้หลายหน่วยที่ผลรวมจะเกิน ก. src="/pictures/wiki/files/55/70c78823302483b6901ad39f68949086.png" border="0">

คุณสมบัติเพิ่มเติม

คุณสมบัติอื่นๆ ทั้งหมดที่มีอยู่ในจำนวนตรรกยะไม่ได้แยกออกมาเป็นคุณสมบัติพื้นฐาน เพราะโดยทั่วไปแล้ว คุณสมบัติเหล่านี้ไม่ได้ขึ้นอยู่กับคุณสมบัติของจำนวนเต็มโดยตรงอีกต่อไป แต่สามารถพิสูจน์ได้บนพื้นฐานของคุณสมบัติพื้นฐานที่กำหนดหรือโดยตรงโดยนิยามของ วัตถุทางคณิตศาสตร์บางอย่าง มีคุณสมบัติเพิ่มเติมมากมาย มันสมเหตุสมผลแล้วที่จะอ้างถึงเพียงไม่กี่คน

Src="/pictures/wiki/files/48/0caf9ffdbc8d6264bc14397db34e8d72.png" border="0">

ตั้งค่าการนับ

การนับจำนวนตรรกยะ

ในการประมาณจำนวนตรรกยะ คุณต้องหาจำนวนสมาชิกของเซต เป็นการง่ายที่จะพิสูจน์ว่าเซตของจำนวนตรรกยะนับได้ ในการทำเช่นนี้ ก็เพียงพอแล้วที่จะให้อัลกอริทึมที่ระบุจำนวนตรรกยะ นั่นคือสร้าง bijection ระหว่างชุดของจำนวนตรรกยะและจำนวนธรรมชาติ

อัลกอริทึมที่ง่ายที่สุดมีดังนี้ มีการรวบรวมตารางเศษส่วนสามัญที่ไม่มีที่สิ้นสุดในแต่ละตาราง ฉัน-th ในแต่ละบรรทัด เจคอลัมน์ th ซึ่งเป็นเศษส่วน เพื่อความชัดเจน จะถือว่าแถวและคอลัมน์ของตารางนี้มีหมายเลขตั้งแต่หนึ่ง เซลล์ตารางจะแสดงแทน ที่ไหน ฉัน- หมายเลขแถวของตารางที่มีเซลล์ตั้งอยู่และ เจ- หมายเลขคอลัมน์

ตารางผลลัพธ์ได้รับการจัดการโดย "งู" ตามอัลกอริทึมอย่างเป็นทางการต่อไปนี้

กฎเหล่านี้จะถูกค้นหาจากบนลงล่าง และตำแหน่งถัดไปจะถูกเลือกโดยการแข่งขันนัดแรก

ในกระบวนการบายพาสนั้น จำนวนตรรกยะใหม่แต่ละจำนวนจะถูกกำหนดให้กับจำนวนธรรมชาติถัดไป นั่นคือเศษส่วน 1 / 1 ถูกกำหนดเป็นหมายเลข 1 เศษส่วน 2 / 1 - หมายเลข 2 เป็นต้น ควรสังเกตว่ามีเพียงเศษส่วนที่ลดไม่ได้เท่านั้นที่มีหมายเลข เครื่องหมายที่เป็นทางการของการลดลงไม่ได้คือความเท่ากันกับเอกภาพของตัวหารร่วมมากของตัวเศษและตัวส่วนของเศษส่วน

ตามอัลกอริทึมนี้ เราสามารถแจกแจงจำนวนตรรกยะที่เป็นบวกได้ทั้งหมด ซึ่งหมายความว่าเซตของจำนวนตรรกยะที่เป็นบวกสามารถนับได้ เป็นเรื่องง่ายที่จะสร้างการเทียบเคียงระหว่างชุดของจำนวนตรรกยะที่เป็นบวกและลบ โดยกำหนดให้กับจำนวนตรรกยะแต่ละตัวที่อยู่ตรงข้ามกัน ที่. เซตของจำนวนตรรกยะที่เป็นลบก็นับได้เช่นกัน สหภาพของพวกเขายังนับได้ด้วยคุณสมบัติของชุดที่นับได้ เซตของจำนวนตรรกยะยังสามารถนับได้ในฐานะยูเนียนของเซตที่นับได้กับเซตจำกัด

ข้อความเกี่ยวกับการนับได้ของชุดจำนวนตรรกยะอาจทำให้เกิดความสับสน เนื่องจากเมื่อมองแวบแรกจะรู้สึกว่ามีจำนวนมากกว่าชุดของจำนวนธรรมชาติมาก ในความเป็นจริง นี่ไม่ใช่กรณี และมีจำนวนธรรมชาติมากพอที่จะแจกแจงจำนวนตรรกยะทั้งหมด

ความไม่เพียงพอของจำนวนตรรกยะ

ด้านตรงข้ามมุมฉากของสามเหลี่ยมดังกล่าวไม่ได้แสดงด้วยจำนวนตรรกยะใดๆ

จำนวนตรรกยะของแบบฟอร์ม 1 / นที่มีขนาดใหญ่ นสามารถวัดปริมาณเล็กน้อยได้ตามอำเภอใจ ข้อเท็จจริงนี้สร้างความรู้สึกหลอกลวงว่าจำนวนตรรกยะสามารถวัดระยะทางทางเรขาคณิตโดยทั่วไปได้ มันง่ายที่จะแสดงว่าไม่เป็นความจริง

หมายเหตุ

วรรณกรรม

• I. คุชนีร์ คู่มือคณิตศาสตร์สำหรับเด็กนักเรียน - เคียฟ: ASTARTA, 1998. - 520 น.
• ป.ล. อเล็กซานดรอฟ ความรู้เบื้องต้นเกี่ยวกับทฤษฎีเซตและโทโพโลยีทั่วไป - ม.: หัว. เอ็ด ฟิสิกส์-คณิต สว่าง เอ็ด "วิทยาศาสตร์", 2520
• I. L. Khmelnitsky ความรู้เบื้องต้นเกี่ยวกับทฤษฎีระบบพีชคณิต

ลิงค์

มูลนิธิวิกิมีเดีย 2553 .

) คือตัวเลขที่มีเครื่องหมายบวกหรือลบ (จำนวนเต็มและเศษส่วน) และศูนย์ แนวคิดเกี่ยวกับจำนวนตรรกยะที่แม่นยำยิ่งขึ้นมีลักษณะดังนี้:

จำนวนตรรกยะ- ตัวเลขที่แสดงด้วยเศษส่วนอย่างง่าย ม./นโดยที่ตัวเศษ มเป็นจำนวนเต็มและส่วน น- จำนวนเต็ม ตัวอย่างเช่น 2/3.

เศษส่วนที่ไม่มีคาบเป็นอนันต์จะไม่รวมอยู่ในชุดของจำนวนตรรกยะ

เอ/บี, ที่ไหน ก∈ Z (กเป็นของจำนวนเต็ม) ข∈ เอ็น (ขเป็นของจำนวนธรรมชาติ)

การใช้จำนวนตรรกยะในชีวิตจริง

ใน ชีวิตจริงชุดของจำนวนตรรกยะใช้ในการนับส่วนของวัตถุที่หารด้วยจำนวนเต็มได้ ตัวอย่างเช่นเค้กหรืออาหารอื่น ๆ ที่หั่นเป็นชิ้น ๆ ก่อนบริโภค หรือเพื่อประเมินความสัมพันธ์เชิงพื้นที่ของวัตถุขยายอย่างคร่าว ๆ

คุณสมบัติของจำนวนตรรกยะ

คุณสมบัติพื้นฐานของจำนวนตรรกยะ

1. ความเป็นระเบียบเรียบร้อย กและ ขมีกฎที่อนุญาตให้คุณระบุความสัมพันธ์ระหว่างพวกเขา 1-แต่และมีเพียงหนึ่งใน 3 ความสัมพันธ์: “<», «>" หรือ "=" กฎนี้คือ - กฎการสั่งซื้อและกำหนดดังนี้:

• 2 จำนวนบวก a=m เป็น /nและ b=m ข /n ขสัมพันธ์กันด้วยความสัมพันธ์เดียวกันกับจำนวนเต็ม 2 จำนวน ม⋅ หมายเหตุและ เมตร ข⋅ n ก;
• 2 จำนวนลบ กและ ขสัมพันธ์กันด้วยความสัมพันธ์เดียวกันกับจำนวนบวก 2 จำนวน |ข|และ |ก|;
• เมื่อไร กบวกและ ข- ติดลบแล้ว ก> ข.

∀ ก ข∈ ถาม(ก ∨ ก> ข∨ ก=ข)

2. การดำเนินการเพิ่มเติม. สำหรับจำนวนตรรกยะทั้งหมด กและ ขมี กฎการรวมซึ่งทำให้พวกเขาสอดคล้องกับจำนวนตรรกยะที่แน่นอน ค. อย่างไรก็ตาม ตัวเลขดังกล่าว ค- นี้ ผลรวมตัวเลข กและ ขและเรียกว่า (ก+ข) ผลรวม.

กฎการสรุปผลดูเหมือนว่า:

ม/n a + m b/n ข =(ม⋅ nb+mb⋅ n ก)/(น⋅ หมายเหตุ).

∀ ก ข∈ ถาม∃ !(ก+ข)∈ ถาม

3. การดำเนินการคูณ. สำหรับจำนวนตรรกยะทั้งหมด กและ ขมี กฎการคูณมันเชื่อมโยงกับจำนวนตรรกยะที่แน่นอน ค. หมายเลข c ถูกเรียก งานตัวเลข กและ ขและแสดงว่า (a⋅b)และกระบวนการค้นหาหมายเลขนี้เรียกว่า การคูณ.

กฎการคูณดูเหมือนว่า: เอ็ม เอ เอ็น เอ⋅ m bn b = m ก⋅ m b n ก⋅ หมายเหตุ.

∀a,b∈Q ∃(a⋅b)∈Q

4. การเปลี่ยนแปลงของลำดับความสัมพันธ์สำหรับจำนวนตรรกยะสามจำนวนใดๆ ก, ขและ คถ้า กน้อย ขและ ขน้อย ค, ที่ กน้อย ค, และถ้า กเท่ากับ ขและ ขเท่ากับ ค, ที่ กเท่ากับ ค.

∀ ก,ข,ค∈ ถาม(ก ∧ ข ⇒ ก ∧ (ก=ข∧ ข=ค⇒ ก = ค)

5. การสลับที่ของการบวก. จากการเปลี่ยนแปลงตำแหน่งของเงื่อนไขผลรวมจะไม่เปลี่ยนแปลง

∀ ก ข∈ Qa+b=b+ก

6. ความเชื่อมโยงของการบวก. ลำดับการบวกของจำนวนตรรกยะ 3 ตัวไม่มีผลกับผลลัพธ์

∀ ก,ข,ค∈ Q(a+b)+c=a+(b+c)

7. การแสดงตนของศูนย์. มีจำนวนตรรกยะเป็น 0 ซึ่งจะรักษาจำนวนตรรกยะอื่น ๆ เมื่อนำมาบวกกัน

∃ 0 ∈ ถาม∀ ก∈ Qa+0=ก

8. การแสดงตนของจำนวนตรงข้าม. จำนวนตรรกยะทุกตัวมีจำนวนตรรกยะตรงข้ามกัน เมื่อบวกกันแล้วจะได้ 0

∀ ก∈ ถาม∃ (-a)∈ Qa+(−a)=0

9. การสับเปลี่ยนของการคูณ. ผลิตภัณฑ์จะไม่เปลี่ยนแปลงโดยการเปลี่ยนตำแหน่งของปัจจัยที่มีเหตุผล

∀ ก ข∈ ถาม⋅ ข=ข⋅ ก

10. ความสัมพันธ์ของการคูณ. ลำดับการคูณของจำนวนตรรกยะ 3 ตัวไม่มีผลกับผลลัพธ์

∀ ก,ข,ค∈ ถาม(ก⋅ ข)⋅ ค=ก⋅ (ข⋅ ค)

11. ความพร้อมของหน่วย. มีจำนวนตรรกยะ 1 มันรักษาจำนวนตรรกยะอื่น ๆ ในกระบวนการคูณ

∃ 1 ∈ ถาม∀ ก∈ ถาม⋅ 1=ก

12. ความพร้อมใช้งาน ตัวเลขซึ่งกันและกัน . จำนวนตรรกยะใดๆ ที่ไม่ใช่ศูนย์จะมีจำนวนตรรกยะผกผัน ซึ่งคูณด้วยเราจะได้ 1 .

∀ ก∈ ถาม∃ ก−1∈ ถาม⋅ ก−1=1

13. การกระจายของการคูณเกี่ยวกับการบวก. การดำเนินการคูณเกี่ยวข้องกับการบวกโดยใช้กฎการกระจาย:

∀ ก,ข,ค∈ ถาม(a+b)⋅ ค=ก⋅ ค+ข⋅ ค

14. การเชื่อมต่อความสัมพันธ์ของลำดับกับการดำเนินการเพิ่มเติม. จำนวนตรรกยะเดียวกันจะถูกบวกเข้าทางด้านซ้ายและขวาของอสมการจำนวนตรรกยะ

∀ ก,ข,ค∈ ถาม ⇒ เอ + ค

15. การเชื่อมโยงความสัมพันธ์ของลำดับกับการดำเนินการคูณ. ด้านซ้ายและด้านขวาของอสมการที่เป็นจำนวนตรรกยะสามารถคูณด้วยจำนวนตรรกยะที่ไม่เป็นลบเดียวกันได้

∀ ก,ข,ค∈ ถาม>0∧ ก ⇒ ก⋅ ค ⋅ ค

16. สัจพจน์ของอาร์คิมิดีส. อะไรก็ตามที่เป็นจำนวนตรรกยะ กมันง่ายที่จะใช้หน่วยจำนวนมากเพื่อให้ผลรวมของพวกเขามากขึ้น ก.

ในบทความนี้เราจะเริ่มศึกษา สรุปตัวเลข. ที่นี่เราให้คำจำกัดความของจำนวนตรรกยะ ให้คำอธิบายที่จำเป็น และยกตัวอย่างของจำนวนตรรกยะ หลังจากนั้นเราจะมุ่งเน้นไปที่วิธีการตรวจสอบว่า หมายเลขที่กำหนดมีเหตุผลหรือไม่

การนำทางหน้า

ความหมายและตัวอย่างจำนวนตรรกยะ

ในส่วนย่อยนี้เราได้ให้คำจำกัดความของจำนวนตรรกยะหลายประการ แม้จะมีความแตกต่างในการใช้ถ้อยคำ แต่คำจำกัดความทั้งหมดเหล่านี้มีความหมายเหมือนกัน: จำนวนตรรกยะรวมจำนวนเต็มและจำนวนเศษส่วนเข้าด้วยกัน เช่นเดียวกับจำนวนเต็มรวมจำนวนธรรมชาติ จำนวนตรงข้าม และจำนวนศูนย์ กล่าวอีกนัยหนึ่ง จำนวนตรรกยะหมายถึงจำนวนเต็มและเศษส่วน

เริ่มต้นด้วย คำจำกัดความของจำนวนตรรกยะซึ่งถือว่าเป็นธรรมชาติที่สุด

จากคำจำกัดความที่ฟังดูแล้ว จำนวนตรรกยะคือ:

• จำนวนธรรมชาติใดๆ n แท้จริงแล้ว จำนวนธรรมชาติใดๆ สามารถแสดงเป็นเศษส่วนธรรมดาได้ ตัวอย่างเช่น 3=3/1
• จำนวนเต็มใดๆ โดยเฉพาะเลขศูนย์ แท้จริงแล้ว จำนวนเต็มใดๆ สามารถเขียนเป็นเศษส่วนร่วมที่เป็นบวกหรือเป็นเศษส่วนร่วมที่เป็นลบ หรือเป็นศูนย์ก็ได้ ตัวอย่างเช่น 26=26/1 , .
• เศษส่วนสามัญใด ๆ (บวกหรือลบ) สิ่งนี้ระบุไว้โดยตรงโดยคำจำกัดความที่กำหนดของจำนวนตรรกยะ
• จำนวนผสมใดๆ อันที่จริง เป็นไปได้เสมอที่จะแทนจำนวนคละเป็นเศษส่วนร่วมที่ไม่เหมาะสม ตัวอย่างเช่น และ .
• เศษส่วนทศนิยมจำกัดหรือเศษส่วนอนันต์ ที่เป็นเช่นนี้เนื่องจากเศษส่วนทศนิยมที่ระบุจะถูกแปลงเป็นเศษส่วนธรรมดา ตัวอย่างเช่น , และ 0,(3)=1/3

เป็นที่ชัดเจนว่าทศนิยมที่ไม่ซ้ำจำนวนอนันต์ใดๆ นั้นไม่ใช่จำนวนตรรกยะ เนื่องจากไม่สามารถแสดงเป็นเศษส่วนร่วมได้

ตอนนี้เราสามารถนำ ตัวอย่างของจำนวนตรรกยะ. ตัวเลข 4, 903, 100,321 เป็นจำนวนตรรกยะ เนื่องจากเป็นจำนวนธรรมชาติ จำนวนเต็ม 58 , −72 , 0 , −833 333 333 เป็นตัวอย่างของจำนวนตรรกยะเช่นกัน เศษส่วนสามัญ 4/9, 99/3 เป็นตัวอย่างของจำนวนตรรกยะเช่นกัน จำนวนตรรกยะยังเป็นตัวเลข

ตัวอย่างข้างต้นแสดงว่ามีทั้งจำนวนตรรกยะที่เป็นบวกและลบ และจำนวนตรรกยะศูนย์ไม่เป็นทั้งบวกและลบ

คำจำกัดความข้างต้นของจำนวนตรรกยะสามารถกำหนดในรูปแบบที่สั้นกว่าได้

คำนิยาม.

สรุปตัวเลขเรียกตัวเลขที่สามารถเขียนเป็นเศษส่วน z/n โดยที่ z เป็นจำนวนเต็ม และ n เป็นจำนวนธรรมชาติ

ให้เราพิสูจน์ว่าคำจำกัดความของจำนวนตรรกยะนี้เทียบเท่ากับคำจำกัดความก่อนหน้า เรารู้ว่าเราสามารถพิจารณาแถบของเศษส่วนเป็นเครื่องหมายของการหาร จากนั้นจากคุณสมบัติของการหารจำนวนเต็มและกฎสำหรับการหารจำนวนเต็ม ความเท่าเทียมกันต่อไปนี้จะตามมา และ นั่นแหละคือข้อพิสูจน์

ให้เรายกตัวอย่างจำนวนตรรกยะตาม คำนิยามนี้. ตัวเลข −5 , 0 , 3 และเป็นจำนวนตรรกยะ เนื่องจากสามารถเขียนเป็นเศษส่วนด้วยตัวเศษจำนวนเต็มและตัวส่วนธรรมชาติของแบบฟอร์มและตามลำดับ

คำจำกัดความของจำนวนตรรกยะสามารถกำหนดได้ในสูตรต่อไปนี้

คำนิยาม.

สรุปตัวเลขเป็นตัวเลขที่สามารถเขียนเป็นเศษส่วนทศนิยมที่มีขอบเขตจำกัดหรือเป็นอนันต์ได้

คำจำกัดความนี้ยังเทียบเท่ากับคำจำกัดความแรก เนื่องจากเศษส่วนธรรมดาใดๆ สอดคล้องกับเศษส่วนทศนิยมที่มีขอบเขตจำกัดหรือเป็นคาบ และในทางกลับกัน และจำนวนเต็มใดๆ สามารถเชื่อมโยงกับเศษส่วนทศนิยมที่มีศูนย์หลังจุดทศนิยม

ตัวอย่างเช่น ตัวเลข 5 , 0 , −13 เป็นตัวอย่างของจำนวนตรรกยะเพราะสามารถเขียนเป็นทศนิยมต่อไปนี้ 5.0 , 0.0 , −13.0 , 0.8 และ −7,(18)

เราจบทฤษฎีในส่วนนี้ด้วยข้อความต่อไปนี้:

• จำนวนเต็มและเศษส่วน (บวกและลบ) ประกอบกันเป็นชุดของจำนวนตรรกยะ
• จำนวนตรรกยะแต่ละจำนวนสามารถแสดงเป็นเศษส่วนด้วยตัวเศษจำนวนเต็มและตัวส่วนตามธรรมชาติ และแต่ละจำนวนนั้นก็คือจำนวนตรรกยะ
• จำนวนตรรกยะทุกตัวสามารถแสดงเป็นเศษส่วนทศนิยมที่มีขอบเขตจำกัดหรือไม่จำกัด และแต่ละเศษส่วนดังกล่าวแทนจำนวนตรรกยะ

ตัวเลขนี้เป็นจำนวนตรรกยะหรือไม่?

ในย่อหน้าที่แล้ว เราพบว่าจำนวนธรรมชาติ จำนวนเต็ม เศษส่วนธรรมดา จำนวนคละ เศษส่วนทศนิยมสุดท้าย และเศษส่วนทศนิยมเป็นจำนวนตรรกยะ ความรู้นี้ช่วยให้เราสามารถ "จดจำ" จำนวนตรรกยะจากชุดตัวเลขที่เขียนได้

แต่จะเป็นอย่างไรถ้าจำนวนที่กำหนดเป็น some หรือ เป็นต้น จะตอบคำถามได้อย่างไรว่าจำนวนดังกล่าวเป็นจำนวนตรรกยะ? ในหลายกรณีเป็นการยากที่จะตอบ ให้เราชี้ให้เห็นทิศทางของความคิด

ถ้ากำหนดเป็นตัวเลข การแสดงออกที่เป็นตัวเลขซึ่งมีเฉพาะจำนวนตรรกยะและเครื่องหมายของการดำเนินการทางคณิตศาสตร์ (+, −, · และ:) ดังนั้นค่าของนิพจน์นี้จึงเป็นจำนวนตรรกยะ สิ่งนี้ตามมาจากวิธีการกำหนดการดำเนินการกับจำนวนตรรกยะ ตัวอย่างเช่น หลังจากดำเนินการทั้งหมดในนิพจน์ เราจะได้จำนวนตรรกยะ 18 .

บางครั้ง หลังจากการทำให้นิพจน์ง่ายขึ้นและรูปแบบที่ซับซ้อนขึ้น จะสามารถระบุได้ว่าจำนวนที่กำหนดเป็นจำนวนตรรกยะหรือไม่

ไปต่อกันเถอะ เลข 2 เป็นจำนวนตรรกยะ เนื่องจากจำนวนธรรมชาติใดๆ เป็นจำนวนตรรกยะ แล้วเบอร์ล่ะ? มันมีเหตุผล? ปรากฎว่าไม่ใช่ - มันไม่ใช่จำนวนตรรกยะ แต่เป็นจำนวนอตรรกยะ (การพิสูจน์ข้อเท็จจริงนี้โดยความขัดแย้งมีอยู่ในตำราพีชคณิตสำหรับชั้นประถมศึกษาปีที่ 8 ซึ่งระบุไว้ด้านล่างในรายการข้อมูลอ้างอิง) ได้รับการพิสูจน์แล้วว่า รากที่สองจาก จำนวนธรรมชาติจะเป็นจำนวนตรรกยะก็ต่อเมื่อรากเป็นจำนวนที่เป็นกำลังสองสมบูรณ์ของจำนวนธรรมชาติ ตัวอย่างเช่น และเป็นจำนวนตรรกยะ เนื่องจาก 81=9 2 และ 1024=32 2 และจำนวน และ ไม่ใช่จำนวนตรรกยะ เนื่องจากเลข 7 และ 199 ไม่ใช่กำลังสองสมบูรณ์ของจำนวนธรรมชาติ

จำนวนตรรกยะหรือไม่? ในกรณีนี้ มันง่ายที่จะเห็นว่า จำนวนนี้เป็นจำนวนตรรกยะ จำนวนตรรกยะหรือไม่? พิสูจน์ได้ว่ารากที่ k ของจำนวนเต็มเป็นจำนวนตรรกยะ ก็ต่อเมื่อจำนวนที่อยู่ใต้เครื่องหมายรูทเป็นเลขยกกำลัง k ของจำนวนเต็ม ดังนั้นจึงไม่ใช่จำนวนตรรกยะ เนื่องจากไม่มีจำนวนเต็มยกกำลังที่ 5 คือ 121

วิธีการขัดแย้งช่วยให้เราพิสูจน์ได้ว่าลอการิทึมของตัวเลขบางตัวไม่ใช่จำนวนตรรกยะด้วยเหตุผลบางประการ ตัวอย่างเช่น ลองพิสูจน์ว่า - ไม่ใช่จำนวนตรรกยะ

สมมติสิ่งที่ตรงกันข้าม นั่นคือ สมมติว่าเป็นจำนวนตรรกยะและสามารถเขียนเป็นเศษส่วนธรรมดาได้ m/n จากนั้น และ ให้ความเท่าเทียมกันดังต่อไปนี้: . ความเท่าเทียมกันครั้งสุดท้ายเป็นไปไม่ได้เนื่องจากอยู่ทางด้านซ้าย ไม่ เลขคู่ 5 n และทางด้านขวามีเลขคู่ 2 ม. ดังนั้น สมมติฐานของเราผิด จึงไม่ใช่จำนวนตรรกยะ

สรุปได้ว่าควรเน้นย้ำว่าเมื่อชี้แจงเหตุผลหรือความไม่ลงตัวของตัวเลขควรละเว้นจากการสรุปอย่างกะทันหัน

ตัวอย่างเช่น เราไม่ควรยืนยันโดยทันทีว่าผลคูณของจำนวนอตรรกยะ π และ e เป็นจำนวนอตรรกยะ นี่เป็น "ราวกับว่าเห็นได้ชัด" แต่ไม่มีการพิสูจน์ สิ่งนี้ทำให้เกิดคำถาม: "เหตุใดผลคูณจึงเป็นจำนวนตรรกยะ" และทำไมไม่ เพราะคุณสามารถยกตัวอย่างจำนวนอตรรกยะได้ ซึ่งผลคูณของจำนวนตรรกยะคือ:

ยังไม่ทราบว่าจำนวนและจำนวนอื่น ๆ เป็นจำนวนตรรกยะหรือไม่ ตัวอย่างเช่น มีจำนวนอตรรกยะซึ่งกำลังอตรรกยะเป็นจำนวนตรรกยะ เพื่อแสดงให้เห็น ให้ระดับของรูปแบบ ฐานของระดับนี้และเลขชี้กำลังไม่ใช่จำนวนตรรกยะ แต่ และ 3 เป็นจำนวนตรรกยะ

บรรณานุกรม.

• คณิตศาสตร์.ชั้นประถมศึกษาปีที่ 6: หนังสือเรียน. สำหรับการศึกษาทั่วไป สถาบัน/[น. ยา Vilenkin และอื่น ๆ ] - แก้ไขครั้งที่ 22 รายได้ - M.: Mnemosyne, 2008. - 288 p.: ป่วย ไอ 978-5-346-00897-2
• พีชคณิต:หนังสือเรียน สำหรับ 8 เซลล์ การศึกษาทั่วไป สถาบัน/[ยุ. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; เอ็ด S. A. Telyakovsky - 16 เอ็ด - ม. : การศึกษา, 2551. - 271 น. : ป่วย. - ไอ 978-5-09-019243-9
• Gusev V. A. , Mordkovich A. G.คณิตศาสตร์ (คู่มือสำหรับผู้สมัครโรงเรียนเทคนิค): Proc. เบี้ยเลี้ยง.-ม.; สูงกว่า โรงเรียน 2527.-351 น. ป่วย