Systém nerovností Je zvykem nazývat libovolnou množinu dvou nebo více nerovností obsahujících neznámou veličinu.

Tuto formulaci názorně ilustrují např. takové systémy nerovností:

Vyřešte soustavu nerovnic - znamená najít všechny hodnoty neznámé proměnné, pro kterou je každá nerovnost systému realizována, nebo dokázat, že žádné takové neexistují .

Tedy pro každého jednotlivce systémové nerovnosti vypočítat neznámou proměnnou. Dále z výsledných hodnot vybere pouze ty, které jsou pravdivé pro první i druhou nerovnost. Při dosazení zvolené hodnoty se tedy obě nerovnosti systému stanou správnými.

Pojďme analyzovat řešení několika nerovností:

Umístěte jednu pod druhou dvojici číselných řad; dát hodnotu nahoru X, pod kterým je první nerovnost o ( X> 1) se stanou pravdivými a ve spodní části hodnota X, které jsou řešením druhé nerovnosti ( X> 4).

Porovnáním údajů na číselné řady, všimněte si, že řešení pro oba nerovnosti bude X> 4. Odpověď, X> 4.

Příklad 2

Výpočet prvního nerovnost dostáváme -3 X< -6, или X> 2, druhý - X> -8, popř X < 8. Затем делаем по аналогии с предыдущим примером. На верхнюю числовую прямую наносим все те значения X, pod kterým první systémová nerovnost a na spodní číselné řadě všechny tyto hodnoty X, pod kterým je realizována druhá nerovnost systému.

Porovnáním dat zjistíme, že obojí nerovnosti budou implementovány pro všechny hodnoty X umístěno od 2 do 8. Soubory hodnot X označovat dvojitá nerovnost 2 < X< 8.

Příklad 3 Pojďme najít

Program pro řešení lineárních, čtvercových a zlomkové nerovnosti nedává jen odpověď na problém, podává podrobné řešení s vysvětlením, tzn. zobrazuje proces řešení za účelem ověření znalostí z matematiky a/nebo algebry.

Pokud je navíc v procesu řešení některé z nerovností nutné řešit např. kvadratická rovnice, pak se zobrazí i jeho podrobné řešení (je součástí spoileru).

Tento program může být užitečný pro studenty středních škol při přípravě kontrolní práce, rodiče kontrolovat řešení nerovností svými dětmi.

Tento program může být užitečný pro studenty středních škol všeobecně vzdělávací školy v rámci přípravy na testy a zkoušky, při ověřování znalostí před Jednotnou státní zkouškou, aby rodiče ovládali řešení mnoha úloh z matematiky a algebry. Nebo je pro vás možná příliš drahé najmout si lektora nebo koupit nové učebnice? Nebo to jen chcete mít hotové co nejdříve? domácí práce matematika nebo algebra? V tomto případě můžete využít i naše programy s detailním řešením.

Tímto způsobem můžete provádět svůj vlastní trénink a/nebo trénovat svůj mladší bratři nebo sestry, přičemž se zvyšuje úroveň vzdělání v oblasti řešených úkolů.

Pravidla pro zadávání nerovností

Jakékoli latinské písmeno může fungovat jako proměnná.
Například: \(x, y, z, a, b, c, o, p, q \) atd.

Čísla lze zadávat jako celá čísla nebo zlomky.
Zlomková čísla lze navíc zadávat nejen ve formě desetinného místa, ale také ve formě obyčejného zlomku.

Pravidla pro zadávání desetinných zlomků.
V desetinných zlomcích lze zlomkovou část od celého čísla oddělit buď tečkou, nebo čárkou.
Můžete například zadat desetinná místa takže: 2,5x - 3,5x^2

Pravidla pro zadávání obyčejných zlomků.
Pouze celé číslo může fungovat jako čitatel, jmenovatel a celá část zlomku.

Jmenovatel nemůže být záporný.

Při zadávání číselného zlomku se čitatel odděluje od jmenovatele znaménkem dělení: /
celá část oddělené od zlomku ampersandem: &
Vstup: 3&1/3 - 5&6/5y +1/7y^2
Výsledek: \(3\frac(1)(3) - 5\frac(6)(5) y + \frac(1)(7)y^2 \)

Při zadávání výrazů lze použít závorky. V tomto případě se při řešení nerovnice nejprve zjednoduší výrazy.
Například: 5(a+1)^2+2&3/5+a > 0,6(a-2)(a+3)

Vyberte požadované znaménko nerovnosti a zadejte polynomy do polí níže.

První nerovnost systému.

Klepnutím na tlačítko změníte typ první nerovnosti.

> >= < <=

Vyřešte soustavu nerovnic

Bylo zjištěno, že některé skripty potřebné k vyřešení tohoto úkolu nebyly načteny a program nemusí fungovat.
Možná máte povolený AdBlock.
V takovém případě jej deaktivujte a obnovte stránku.

V prohlížeči máte vypnutý JavaScript.
Aby se řešení objevilo, musí být povolen JavaScript.
Zde je návod, jak povolit JavaScript ve vašem prohlížeči.

Protože Existuje spousta lidí, kteří chtějí problém vyřešit, váš požadavek je ve frontě.
Po několika sekundách se řešení objeví níže.
Čekejte prosím sek...

jestli ty zaznamenal chybu v řešení, pak o tom můžete napsat do Formuláře zpětné vazby .
Nezapomeň uveďte jaký úkol ty rozhodneš co zadejte do polí.

Naše hry, hádanky, emulátory:

Trochu teorie.

Systémy nerovnic s jednou neznámou. Číselná rozpětí

V 7. třídě jste se seznámili s pojmem soustava a naučili se řešit soustavy lineárních rovnic o dvou neznámých. O systémech bude řeč dále. lineární nerovnosti s jednou neznámou. Množiny řešení soustav nerovnic lze zapisovat pomocí intervalů (intervaly, polointervaly, segmenty, paprsky). Dozvíte se také o zápisu číselných intervalů.

Pokud je v nerovnostech \(4x > 2000 \) a \(5x \leq 4000 \) neznámé číslo x stejné, pak se tyto nerovnosti uvažují společně a říká se, že tvoří systém nerovností: $$ \left\ (\začátek( pole)(l) 4x > 2000 \\ 5x \leq 4000 \end(pole)\vpravo.$$

Složená závorka ukazuje, že potřebujete najít takové hodnoty x, pro které se obě nerovnosti systému změní na skutečné číselné nerovnosti. Tento systém je příkladem systému lineárních nerovností s jednou neznámou.

Řešením soustavy nerovnic s jednou neznámou je hodnota neznámé, při které se všechny nerovnosti soustavy mění ve skutečné číselné nerovnosti. Řešit systém nerovností znamená najít všechna řešení tohoto systému nebo zjistit, že žádná neexistují.

Nerovnosti \(x \geq -2 \) a \(x \leq 3 \) lze zapsat jako dvojitou nerovnost: \(-2 \leq x \leq 3 \).

Řešení systémů nerovností s jednou neznámou jsou různá číselné sady. Tyto sady mají jména. Takže na reálné ose je množina čísel x taková, že \(-2 \leq x \leq 3 \) je reprezentována úsečkou s konci v bodech -2 a 3.

-2

3

Jestliže \(a je segment a je označen [a; b]

Pokud \(interval a označíme (a; b)

Množiny čísel \(x \) splňující nerovnosti \(a \leq x v polovičních intervalech a jsou označeny [a; b) a (a; b] v tomto pořadí

Nazývají se segmenty, intervaly, polointervaly a paprsky číselné intervaly.

Číselné intervaly lze tedy specifikovat ve formě nerovností.

Řešením nerovnosti se dvěma neznámými je dvojice čísel (x; y), která tuto nerovnost promění ve skutečnou číselnou nerovnost. Vyřešit nerovnici znamená najít množinu všech jejích řešení. Řešení nerovnice x > y tedy budou například dvojice čísel (5; 3), (-1; -1), protože \(5 \geq 3 \) a \(-1 \geq - 1\)

Řešení soustav nerovnic

Už jste se naučili, jak řešit lineární nerovnosti s jednou neznámou. Vědět, co je systém nerovností a řešení systému. Proces řešení soustav nerovnic s jednou neznámou vám tedy nebude činit potíže.

A přesto si připomínáme: Chcete-li vyřešit systém nerovností, musíte vyřešit každou nerovnost samostatně a pak najít průsečík těchto řešení.

Například původní systém nerovností byl zredukován do podoby:
$$ \left\(\begin(pole)(l) x \geq -2 \\ x \leq 3 \end(pole)\right. $$

Chcete-li vyřešit tento systém nerovností, označte řešení každé nerovnosti na reálné ose a najděte jejich průsečík:

-2

3

Průsečík je segment [-2; 3] - jedná se o řešení původní soustavy nerovností.

řešení nerovnosti v režimu online řešení téměř jakákoli daná nerovnost online. Matematický nerovnosti onlineřešit matematiku. Najděte rychle řešení nerovnosti v režimu online. Stránka www.site vám umožňuje najít řešení téměř jakýkoli daný algebraický, trigonometrický nebo transcendentní nerovnost online. Při studiu téměř jakéhokoli oboru matematiky na různé fáze se musí rozhodnout nerovnosti online. Abyste dostali odpověď okamžitě, a hlavně přesnou odpověď, potřebujete zdroj, který vám to umožní. Díky www.site řešit nerovnosti online bude trvat několik minut. Hlavní výhoda www.site při řešení matematických nerovnosti online- je rychlost a přesnost vydané odpovědi. Stránka je schopna vyřešit jakékoli algebraické nerovnosti online, trigonometrické nerovnosti online, transcendentální nerovnosti online, stejně jako nerovnosti s neznámými parametry v režimu online. nerovnosti slouží jako výkonný matematický aparát řešení praktické úkoly. S pomocí matematické nerovnosti lze vyjádřit fakta a vztahy, které se na první pohled mohou zdát matoucí a složité. neznámé množství nerovnosti lze nalézt formulací problému v matematický jazyk ve formuláři nerovnosti a rozhodni se přijatý úkol v režimu online na webu www.site. Žádný algebraická nerovnost, trigonometrická nerovnost nebo nerovnosti obsahující transcendentální funkce vás snadno rozhodni se online a získejte správnou odpověď. Při studiu přírodních věd člověk nevyhnutelně naráží na potřebu řešení nerovností. V tomto případě musí být odpověď přesná a musí být přijata okamžitě v režimu online. Proto pro řešit matematické nerovnosti online doporučujeme stránku www.site, která se stane vaší nepostradatelnou kalkulačkou řešit algebraické nerovnosti online, trigonometrické nerovnosti online, stejně jako transcendentální nerovnosti online nebo nerovnosti s neznámými parametry. Pro praktické problémy hledání intravol řešení různých matematické nerovnosti zdroj www.. Řešení nerovnosti online sami, je užitečné zkontrolovat přijatou odpověď pomocí online řešení nerovnosti na webu www.site. Nerovnici je nutné správně zapsat a okamžitě získat online řešení, načež zbývá jen porovnat odpověď s vaším řešením nerovnosti. Kontrola odpovědi nezabere déle než minutu, dost řešit nerovnosti online a porovnejte odpovědi. To vám pomůže vyhnout se chybám rozhodnutí a odpověď včas opravte řešení nerovností online zda algebraický, trigonometrický, transcendentní nebo nerovnost s neznámými parametry.

Nerovnice jsou dvě čísla nebo matematické výrazy spojené jedním ze znamének: > (více, v případě striktních nerovností),< (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).

nerovnost je lineární za stejných podmínek jako rovnice: obsahuje proměnné pouze do prvního stupně a neobsahuje součiny proměnných.

Řešení lineárních nerovnic a soustav lineárních nerovnic je nerozlučně spjato s jejich geometrickým významem: řešením lineární nerovnice je určitá polorovina, na kterou je celá rovina rozdělena přímkou, jejíž rovnice je dána vztahem lineární nerovnost. Tuto polorovinu a v případě soustavy lineárních nerovností část roviny ohraničenou několika přímkami je třeba najít na výkrese.

Mnoho ekonomických problémů je redukováno na řešení systémů lineárních nerovností s velkým počtem proměnných, zejména problémy lineárního programování, ve kterých je požadováno najít maximum nebo minimum funkce.

Řešení soustav lineárních nerovnic s libovolným počtem neznámých

Nejprve analyzujme lineární nerovnosti v rovině. Uvažujme jednu nerovnost se dvěma proměnnými a:

,

kde jsou koeficienty proměnných (nějaká čísla), je volný člen (také nějaké číslo).

Jedna nerovnost se dvěma neznámými, jako rovnice, má nekonečný počet řešení. Řešením této nerovnosti je dvojice čísel vyhovující této nerovnosti. Geometricky je množina řešení nerovnice znázorněna jako polorovina ohraničená přímkou

,

kterou budeme nazývat hraniční čára.

Krok 1. Sestrojte přímku ohraničující množinu řešení lineární nerovnice

K tomu potřebujete znát dva libovolné body této přímky. Najdeme průsečíky se souřadnicovými osami. Souřadnice křižovatky A je nula (obrázek 1). Číselné hodnoty na osách na tomto obrázku se vztahují k příkladu 1, který budeme analyzovat ihned po této teoretické odbočce.

Úsečku najdeme tak, že jako soustavu vyřešíme rovnici přímky s rovnicí osy.

Najdeme průsečík s osou:

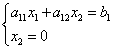
Dosazením hodnoty do první rovnice dostaneme

kde .

Našli jsme tedy úsečku bodu A .

Najdeme souřadnice průsečíku s osou.

Bod úsečky B rovná se nule. Vyřešme rovnici hraniční čáry rovnicí souřadnicové osy:

,

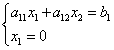
odtud souřadnice bodu B: .

Krok 2. Nakreslete čáru, která ohraničuje množinu řešení nerovnosti. Znát body A a B průsečík hraniční čáry se souřadnicovými osami, můžeme tuto čáru nakreslit. Přímka (opět obrázek 1) rozděluje celou rovinu na dvě části ležící vpravo a vlevo (nad a pod) této přímky.

Krok 3. Určete, která z polorovin je řešením této nerovnosti. K tomu potřebujeme dosadit počátek souřadnic (0; 0) do této nerovnosti. Vyhovují-li souřadnice počátku nerovnosti, pak řešením nerovnosti je polorovina, ve které se nachází počátek. Pokud souřadnice nevyhovují nerovnosti, pak řešením nerovnosti je polorovina, která neobsahuje počátek. Polorovinu řešení nerovnice budeme označovat tahy od přímky uvnitř poloroviny, jako na obrázku 1.

Pokud vyřešíme soustavu lineárních nerovnic, pak se každý krok provede pro každou z nerovností systému.

Příklad 1 Vyřešte nerovnost

Řešení. Nakreslíme rovnou čáru

Dosazením přímky do rovnice dostaneme a dosazením dostaneme. Souřadnice průsečíků s osami tedy budou A(3; 0) , B(0; 2). Těmito body nakreslete přímku (opět obrázek 1).

Volíme polorovinu řešení nerovnice. K tomu dosadíme souřadnice začátku (0; 0) do nerovnosti:

získáme , tj. souřadnice počátku splňují tuto nerovnost. Řešením nerovnosti je tedy polorovina obsahující počátek, tj. levá (nebo spodní) polorovina.

Pokud by tato nerovnost byla přísná, to znamená, že by měla formu

pak by body hraniční čáry nebyly řešením, protože nesplňují nerovnost.

Nyní zvažte systém lineárních nerovností se dvěma neznámými:

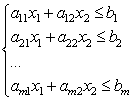
Každá z nerovností tohoto systému v rovině definuje polorovinu. Systém lineárních nerovností se nazývá konzistentní, pokud má alespoň jedno řešení, a nekonzistentní, pokud nemá žádná řešení. Řešením soustavy lineárních nerovnic je libovolná dvojice čísel (), která vyhoví všem nerovnostem této soustavy.

Geometricky je řešením soustavy lineárních nerovnic množina bodů, které splňují všechny nerovnosti soustavy, tedy společná část výsledných polorovin. Geometricky tedy v obecném případě může být řešení znázorněno jako určitý mnohoúhelník, v konkrétním případě to může být úsečka, úsečka a dokonce i bod. Pokud je soustava lineárních nerovností nekonzistentní, pak v rovině není jediný bod, který by vyhovoval všem nerovnostem soustavy.

Příklad 2

Řešení. Je tedy potřeba najít mnohoúhelník řešení tohoto systému nerovnic. Sestrojme hraniční čáru pro první nerovnost, tedy úsečku, a hraniční čáru pro druhou nerovnost, tedy přímku.

Děláme to krok za krokem, jak bylo ukázáno v teoretickém odkazu a v příkladu 1, zejména proto, že v příkladu 1 byla vytvořena hraniční čára pro nerovnost, která je první v tomto systému.

Poloroviny řešení odpovídající nerovnostem tohoto systému jsou na obrázku 2 vystínovány směrem dovnitř. Společnou součástí řešení polorovin je otevřený úhel ABC. To znamená, že množina bodů v rovině, které tvoří otevřený úhel ABC, je řešením první i druhé nerovnice soustavy, tedy je řešením soustavy dvou lineárních nerovnic. Jinými slovy, souřadnice libovolného bodu z této množiny splňují obě nerovnosti systému.

Příklad 3 Vyřešte soustavu lineárních nerovnic

Řešení. Sestrojme hraniční čáry odpovídající nerovnicím soustavy. Toho dosáhneme podle kroků uvedených v teoretickém pozadí pro každou nerovnost. Nyní definujeme poloroviny řešení pro každou nerovnici (obrázek 3).

Poloroviny řešení odpovídající nerovnostem dané soustavy jsou zastíněny dovnitř. Průsečík polorovin řešení je znázorněn, jak je znázorněno na obrázku, ve tvaru čtyřúhelníku ABCE. Zjistili jsme, že polygon řešení soustavy lineárních nerovnic se dvěma proměnnými je čtyřúhelník ABCE .

Vše výše popsané o soustavách lineárních nerovnic se dvěma neznámými platí i pro soustavu nerovnic s libovolným počtem neznámých, jen s tím rozdílem, že řešení nerovnice s n neznámo bude totalita nčísla () splňující všechny nerovnosti a místo hraniční čáry bude hraniční nadrovina n-rozměrný prostor. Řešením bude mnohostěn řešení (simplex) ohraničený nadrovinami.

viz také Grafické řešení úlohy lineárního programování, Kanonická forma úloh lineárního programování

Systém omezení pro takový problém se skládá z nerovností ve dvou proměnných:
a účelová funkce má tvar F = C 1 X + C 2 y, která má být maximalizována.

Odpovězme na otázku: jaké dvojice čísel ( X; y) jsou řešení soustavy nerovností, tj. splňují každou z nerovností současně? Jinými slovy, co to znamená vyřešit systém graficky?
Nejprve musíte pochopit, jaké je řešení jedné lineární nerovnosti se dvěma neznámými.
Řešit lineární nerovnost se dvěma neznámými znamená určit všechny dvojice hodnot neznámých, pro které je nerovnost splněna.
Například nerovnost 3 X – 5y≥ 42 uspokojí dvojice ( X , y): (100, 2); (3, –10) atd. Problém je najít všechny takové dvojice.
Zvažte dvě nerovnosti: sekera + podle≤ C, sekera + podle≥ C. Rovný sekera + podle = C rozděluje rovinu na dvě poloroviny tak, aby souřadnice bodů jedné z nich vyhovovaly nerovnosti sekera + podle >C a další nerovnost sekera + +podle <C.
Opravdu, vezměte bod pomocí souřadnic X = X 0; pak bod ležící na přímce a mající úsečku X 0 , má pořadnici

Pro jistotu A<0, b>0, C>0. Všechny body s úsečkou X 0 výše P(např. tečka M), mít y M>y 0 a všechny body pod bodem P, s úsečkou X 0, mít yN<y 0 Protože X 0 je libovolný bod, pak budou na jedné straně úsečky vždy body, pro které sekera+ podle > C, tvořící polorovinu, a na druhé straně body, pro které sekera + podle< C.

Obrázek 1

Znaménko nerovnosti v polorovině závisí na číslech A, b , C.
Z toho vyplývá následující metoda pro grafické řešení soustav lineárních nerovnic ve dvou proměnných. K vyřešení systému potřebujete:

1. Pro každou nerovnost zapište rovnici odpovídající dané nerovnosti.
2. Sestrojte čáry, které jsou grafy funkcí daných rovnicemi.
3. Pro každou přímku určete polorovinu, která je dána nerovností. Chcete-li to provést, vezměte libovolný bod, který neleží na přímce, dosaďte jeho souřadnice do nerovnosti. pokud je nerovnost pravdivá, pak je řešením původní nerovnosti polorovina obsahující zvolený bod. Pokud je nerovnost nepravdivá, pak polorovina na druhé straně přímky je množinou řešení této nerovnosti.
4. Pro řešení soustavy nerovnic je nutné najít oblast průniku všech polorovin, které jsou řešením každé nerovnosti v soustavě.

Tato oblast se může ukázat jako prázdná, pak systém nerovností nemá řešení, je nekonzistentní. Jinak je prý systém kompatibilní.
Řešením může být konečné číslo a nekonečná množina. Oblast může být uzavřený polygon nebo může být neomezená.

Podívejme se na tři relevantní příklady.

Příklad 1. Graficky vyřešte soustavu:
X + y- 1 ≤ 0;
–2X- 2y + 5 ≤ 0.

• uvažujme rovnice x+y–1=0 a –2x–2y+5=0 odpovídající nerovnicím;
• sestrojme přímky dané těmito rovnicemi.

Obrázek 2

Definujme poloroviny dané nerovnostmi. Vezměte libovolný bod, nechť (0; 0). Zvážit X+ y- 1 0 dosadíme bod (0; 0): 0 + 0 – 1 ≤ 0. tedy v polorovině, kde bod (0; 0) leží, X + y – 1 ≤ 0, tj. polorovina ležící pod přímkou ​​je řešením první nerovnosti. Dosazením tohoto bodu (0; 0) do druhého dostaneme: –2 ∙ 0 – 2 ∙ 0 + 5 ≤ 0, tzn. v polorovině, kde leží bod (0; 0), -2 X – 2y+ 5≥ 0 a byli jsme dotázáni, kde -2 X – 2y+ 5 ≤ 0 tedy v jiné polorovině - v té nad přímkou.
Najděte průsečík těchto dvou polorovin. Přímky jsou rovnoběžné, roviny se tedy nikde neprotínají, což znamená, že soustava těchto nerovnic nemá řešení, je nekonzistentní.

Příklad 2. Najděte graficky řešení soustavy nerovnic:

Obrázek 3
1. Zapište rovnice odpovídající nerovnicím a sestrojte přímky.
X + 2y– 2 = 0

X	2	0
y	0	1

y – X – 1 = 0

X	0	2
y	1	3

y + 2 = 0;
y = –2.
2. Po zvolení bodu (0; 0) určíme znaménka nerovností v polorovinách:
0 + 2 ∙ 0 – 2 ≤ 0, tzn. X + 2y– 2 ≤ 0 v polorovině pod přímkou;
0 – 0 – 1 ≤ 0, tzn. y –X– 1 ≤ 0 v polorovině pod přímkou;
0 + 2 = 2 ≥ 0, tj. y+ 2 ≥ 0 v polorovině nad přímkou.
3. Průsečíkem těchto tří polorovin bude plocha, která je trojúhelníkem. Není těžké najít vrcholy oblasti jako průsečíky odpovídajících čar


Takto, ALE(–3; –2), V(0; 1), Z(6; –2).

Uvažujme ještě jeden příklad, ve kterém výsledná doména řešení systému není omezena.