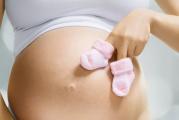
Řešení integrálu online. Najděte neurčitý integrál: počátky začátků, příklady řešení
Nalezení neurčitého integrálu (souboru primitivních nebo „antiderivativ“) znamená obnovení funkce ze známé derivace této funkce. Obnovená sada primitivních prvků F(X) + S pro funkci F(X) bere v úvahu integrační konstantu C. Podle rychlosti pohybu hmotného bodu (derivace) lze obnovit pohybový zákon tohoto bodu (původní); podle zrychlení pohybu bodu - jeho rychlosti a zákona pohybu. Jak je vidět, integrace je široké pole pro působení Sherlocka Holmese z fyziky. Ano a v ekonomice je mnoho pojmů zastoupeno prostřednictvím funkcí a jejich derivátů, a proto je možné např. určitý okamžikčas (derivát) k obnovení objemu produktů vyrobených v odpovídajícím čase.
K nalezení neurčitého integrálu je potřeba poměrně malý počet základních integračních vzorců. Ale proces hledání je mnohem obtížnější než pouhá aplikace těchto vzorců. Veškerá složitost se netýká integrace, ale dovedení integrovatelného výrazu do takové formy, která umožňuje najít neurčitý integrál pomocí výše uvedených základních vzorců. To znamená, že pro zahájení praxe integrace musíte aktivovat výsledky získané v střední škola schopnost transformace výrazu.
Naučíme se hledat integrály pomocí vlastnosti a tabulka neurčitých integrálů z lekce o základních pojmech tohoto tématu (otevře se v novém okně).
Existuje několik metod, jak najít integrál, z nichž variabilní metoda náhrady A metoda integrace po částech- povinná gentlemanská sada pro každého, kdo úspěšně prošel vyšší matematikou. Je však užitečnější a příjemnější začít se učit integraci pomocí expanzní metody založené na následujících dvou větách o vlastnostech neurčitého integrálu, které si zde pro pohodlí zopakujeme.
Věta 3. Konstantní činitel v integrandu lze vyjmout ze znaménka neurčitého integrálu, tzn.
Věta 4. Neurčitý integrál algebraického součtu konečného počtu funkcí se rovná algebraickému součtu neurčitých integrálů těchto funkcí, tzn.
 (2)
(2)
Kromě toho může být při integraci užitečné následující pravidlo: pokud výraz integrandu obsahuje konstantní faktor, pak se vyjádření primitivního prvku vynásobí reciprokou konstantního faktoru, tj.
![]() (3)
(3)
Vzhledem k tomu, že tato lekce je úvodem do řešení integračních problémů, je důležité poznamenat dvě věci, které již existují počáteční fáze, nebo o něco později vás může překvapit. Překvapení je způsobeno skutečností, že integrace je inverzní operací derivace a neurčitý integrál lze právem nazvat "antiderivační".
První věc, která by se při integraci neměla divit. V tabulce integrálů existují vzorce, které nemají mezi vzorci tabulky derivací obdoby . Jedná se o následující vzorce:
![]()
![]()
Je však možné ověřit, že derivace výrazů na pravé straně těchto vzorců se shodují s odpovídajícími integrandy.
Druhá věc, nedivit se při integraci. Ačkoli derivace jakékoli elementární funkce je také elementární funkcí, neurčité integrály některých elementárních funkcí již nejsou elementárními funkcemi . Příklady takových integrálů jsou:
![]()
![]()
![]()
K vývoji integrační techniky budou užitečné následující dovednosti: redukce zlomků, dělení polynomu v čitateli zlomku monočlenem ve jmenovateli (pro získání součtu neurčitých integrálů), převod odmocnin na stupeň, násobení monočlenu polynom, zvyšující se na mocninu. Tyto dovednosti jsou potřebné k transformaci integrandu, která by měla vyústit v součet integrálů přítomných v tabulce integrálů.
Společné hledání neurčitých integrálů
Příklad 1 Najděte neurčitý integrál
![]() .
.
Řešení. Ve jmenovateli integrandu vidíme polynom, ve kterém je x na druhou. To je téměř jisté znamení, že lze použít tabulkový integrál 21 (s arkus tangens výsledku). Ze jmenovatele vyjmeme součinitel dva (taková vlastnost integrálu je - ze znaménka integrálu lze vyjmout konstantní součinitel, bylo to uvedeno výše jako věta 3). Výsledek toho všeho:
Nyní je jmenovatelem součet druhých mocnin, což znamená, že můžeme aplikovat zmíněný tabulkový integrál. Konečně dostáváme odpověď:
![]() .
.
Příklad 2 Najděte neurčitý integrál
Řešení. Opět aplikujeme větu 3 - vlastnost integrálu, na základě které lze ze znaménka integrálu vyjmout konstantní faktor:
Na integrand použijeme vzorec 7 z tabulky integrálů (s proměnným stupněm):
![]() .
.
Výsledné zlomky zredukujeme a máme konečnou odpověď:
Příklad 3 Najděte neurčitý integrál
![]()
Řešení. Aplikujeme-li nejprve větu 4 a poté větu 3 o vlastnostech, zjistíme, že tento integrál je součtem tří integrálů:
Všechny tři získané integrály jsou tabulkové. K tomu použijeme vzorec (7) z tabulky integrálů n = 1/2, n= 2 a n= 1/5 a pak
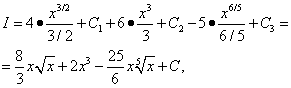
![]()
kombinuje všechny tři libovolné konstanty, které byly zavedeny při hledání tří integrálů. Proto by v podobných situacích měla být zavedena pouze jedna libovolná konstanta (konstanta) integrace.
Příklad 4 Najděte neurčitý integrál
Řešení. Když je ve jmenovateli integrandu jednočlenný člen, můžeme čitatele vydělit jmenovatelem člen po členu. Původní integrál se změnil na součet dvou integrálů:
![]() .
.
Abychom mohli použít tabulkový integrál, převedeme kořeny na mocniny a zde je konečná odpověď:

Pokračujeme v hledání neurčitých integrálů společně
Příklad 7 Najděte neurčitý integrál

Řešení. Pokud integrand převedeme na druhou mocninu binomu a vydělíme čitatel jmenovatelem člen členem, pak se původní integrál stane součtem tří integrálů.
Je předložen přehled metod pro výpočet neurčitých integrálů. Jsou uvažovány hlavní metody integrace, které zahrnují integraci součtu a rozdílu, vyjmutí konstanty ze znaménka integrálu, změnu proměnné a integraci po částech. Také uvažováno speciální metody a techniky pro integraci zlomků, odmocnin, trigonometrických a exponenciálních funkcí.
Primitivní a neurčitý integrál
Primitivní funkce F(x) funkce f(x) je taková funkce, jejíž derivace je rovna f(x) :
F′(x) = f(x), x ∈ ∆,
Kde Δ
- interval, na kterém je tato rovnice splněna.
Množina všech primitivních prvků se nazývá neurčitý integrál:
,
kde C je konstanta nezávislá na x .
Základní vzorce a metody integrace
Tabulka integrálů
Konečným cílem výpočtu neurčitých integrálů je pomocí transformací přivést daný integrál k výrazu obsahujícímu jednoduché nebo tabulkové integrály.
Viz tabulka integrálů >>>
Součtové (rozdílové) integrační pravidlo
Vyjmutí konstanty ze znaménka integrálu
Nechť c je konstanta nezávislá na x. Pak jej lze vyjmout ze znaménka integrálu:
Variabilní substituce
Nechť x je funkcí proměnné t , x = φ(t) , pak
.
Nebo naopak, t = φ(x) ,
.
Pomocí změny proměnné můžete vypočítat nejen jednoduché integrály, ale také zjednodušit výpočet složitějších.
Pravidlo integrace po částech
Integrace zlomků (racionální funkce)
Zavedeme notaci. Nechť P k (x), Q m (x), R n (x) označují polynomy stupňů k, m, n vzhledem k proměnné x .
Uvažujme integrál sestávající ze zlomku polynomů (takzvaná racionální funkce):
Pokud k ≥ n, musíte nejprve vybrat celočíselnou část zlomku:
.
Integrál polynomu S k-n (x) se vypočítá z tabulky integrálů.
Integrál zůstává:
, kde m< n
.
Abychom jej vypočítali, musí být integrand rozložen na jednoduché zlomky.
Chcete-li to provést, musíte najít kořeny rovnice:
Qn (x) = 0.
Pomocí získaných kořenů musíte představovat jmenovatele jako součin faktorů:
Q n (x) = s (x-a) n a (x-b) n b ... (x 2 +ex+f) n e (x 2 +gx+k) n g ....
Zde s je koeficient pro x n , x 2 + ex + f > 0 , x 2 + gx + k > 0 , ... .
Poté zlomek rozložte na nejjednodušší:
Integrováním získáme výraz složený z jednodušších integrálů.
Integrály formuláře
jsou redukovány na tabulkovou substituci t = x - a .
Zvažte integrál:
Pojďme transformovat čitatel:
.
Dosazením do integrandu získáme výraz, který obsahuje dva integrály:
,
.
Nejprve se substituce t \u003d x 2 + ex + f zredukuje na tabulku.
Druhý, podle redukčního vzorce:
se redukuje na integrál
Přivedeme jeho jmenovatele na součet čtverců:
.
Pak substitucí integrál
je uvedena i v tabulce.
Integrace iracionálních funkcí
Zavedeme notaci. Nechť R(u 1 , u 2 , ... , u n) označuje racionální funkci proměnných u 1 , u 2 , ... , u n . To znamená
,
kde P, Q jsou polynomy v proměnných u 1 , u 2 , ... , u n .
Zlomková lineární iracionalita
Zvažte integrály tvaru:
,
kde - racionální čísla, m 1 , n 1 , ..., m s , n s jsou celá čísla.
Nechť n je společný jmenovatel čísel r 1 , ..., r s .
Potom se integrál redukuje na integrál racionálních funkcí substitucí:
.
Integrály z diferenciálních binomů
Zvažte integrál:
,
kde m, n, p jsou racionální čísla, a, b jsou reálná čísla.
Takové integrály se ve třech případech redukují na integrály racionálních funkcí.
1) Je-li p celé číslo. Substituce x = t N , kde N je společným jmenovatelem zlomků ma n .
2) If je celé číslo. Substituce a x n + b = t M , kde M je jmenovatel p .
3) If je celé číslo. Substituce a + b x - n = t M , kde M je jmenovatel p .
Pokud žádné ze tří čísel není celé číslo, pak podle Čebyševovy věty nelze integrály tohoto tvaru vyjádřit konečnou kombinací elementárních funkcí.
V některých případech může být užitečné nejprve snížit integrál na vhodnější hodnoty m a p . To lze provést pomocí vzorců obsazení:
;
.
Integrály obsahující druhou odmocninu čtvercového trinomu
Zde uvažujeme integrály tvaru:
,
Eulerovy substituce
Takové integrály lze redukovat na integrály racionálních funkcí jedné ze tří Eulerových substitucí:
, pro a > 0;
, pro c > 0;
, kde x 1 je kořen rovnice a x 2 + b x + c = 0. Pokud má tato rovnice skutečné kořeny.
Trigonometrické a hyperbolické substituce
Přímé metody
Ve většině případů vedou Eulerovy substituce k delším výpočtům než přímé metody. Pomocí přímých metod je integrál redukován na jeden z následujících typů.
píši
Integrál formuláře:
,
kde P n (x) je polynom stupně n.
Takové integrály se nalézají metodou neurčitých koeficientů pomocí identity:
Diferencováním této rovnice a přirovnáním levé a pravé strany nalezneme koeficienty A i .
II typ
Integrál formuláře:
,
kde P m (x) je polynom stupně m.
Substituce t = (x - a) -1 tento integrál je redukován na předchozí typ. Pokud m ≥ n, pak by zlomek měl mít celočíselnou část.
III typ
Třetí a nejobtížnější typ:
.
Zde musíte provést náhradu:
.
Potom bude mít integrál tvar:
.
Dále musí být konstanty α, β zvoleny tak, aby koeficienty v t zmizely:
B = 0, B1 = 0.
Pak se integrál rozloží na součet integrálů dvou typů:
;
,
které jsou integrovány substitucemi:
z2 \u003d A1t2 + C1;
y2 \u003d A1 + C1t-2.
Obecný případ
Integrace transcendentálních (trigonometrických a exponenciálních) funkcí
Předem poznamenáváme, že ty metody, které jsou použitelné pro goniometrické funkce, jsou použitelné také pro hyperbolické funkce. Z tohoto důvodu nebudeme uvažovat samostatně integraci hyperbolických funkcí.
Integrace racionálních goniometrických funkcí cos x a sin x
Zvažte integrály goniometrických funkcí tvaru:
,
kde R je racionální funkce. To může také zahrnovat tangens a kotangens, které by měly být převedeny přes sinus a kosinus.
Při integraci takových funkcí je užitečné mít na paměti tři pravidla:
1) pokud R( cosx, sinx) násobeno -1 od změny znaménka před jednou z veličin cos x nebo hřích x, pak je užitečné označovat další z nich t .
2) pokud R( cosx, sinx) se nezmění od změny znaménka ve stejnou dobu předtím cos x A hřích x, pak je užitečné dát tan x = t nebo ctg x = t.
3) substituce ve všech případech vede k integrálu racionálního zlomku. Bohužel toto nahrazení vede k delším výpočtům než předchozí, pokud je to možné.
Součin mocninných funkcí cos x a sin x
Zvažte integrály tvaru:
Jestliže m a n jsou racionální čísla, pak jedna z permutací t = hřích x nebo t= cos x integrál se redukuje na integrál diferenciálního binomu.
Jestliže m a n jsou celá čísla, pak se integrály počítají integrací po částech. Výsledkem jsou následující redukční vzorce:
;
;
;
.
Integrace po částech
Aplikace Eulerova vzorce
Pokud je integrand lineární vzhledem k jedné z funkcí
cos sekera nebo sinax, pak je vhodné použít Eulerův vzorec:
e iax = cos sekera + isin sekera(kde i 2 = - 1
),
nahrazením této funkce eiax a zvýraznění skutečného (při nahrazení cos sekera) nebo imaginární část (při výměně sinax) z výsledku.
Reference:
N.M. Gunther, R.O. Kuzmin, Sbírka úloh z vyšší matematiky, Lan, 2003.
Proces řešení integrálů ve vědě nazývaný "matematika" se nazývá integrace. Pomocí integrace můžete najít některé fyzikální veličiny: plochu, objem, hmotnost těles a mnoho dalšího.
Integrály jsou neurčité a určité. Zvažte tvar určitého integrálu a pokuste se pochopit jeho fyzikální význam. Vypadá následovně: $$ \int ^a _b f(x) dx $$. Výrazná vlastnost psaní určitého integrálu od neurčitého v tom smyslu, že existují limity integrace a a b. Nyní zjistíme, k čemu slouží a co znamená určitý integrál. V geometrickém smyslu se takový integrál rovná ploše obrázku ohraničené křivkou f(x), čarami a a b a osou Ox.
Z obr. 1 je vidět, že určitý integrál je stejná plocha, která je stínovaná v šedé barvě. Pojďme si to ověřit na jednoduchém příkladu. Najděte oblast obrázku na obrázku níže pomocí integrace a poté ji vypočítejte obvyklým způsobem vynásobením délky šířkou.

Obrázek 2 ukazuje, že $ y=f(x)=3 $, $ a=1, b=2 $. Nyní je dosadíme do definice integrálu, dostaneme, že $$ S=\int _a ^b f(x) dx = \int _1 ^2 3 dx = $$ $$ =(3x) \Big|_1 ^2 =(3 \ cdot 2)-(3 \cdot 1)=$$ $$=6-3=3 \text(jednotka)^2 $$ Proveďme kontrolu obvyklým způsobem. V našem případě délka = 3, šířka tvaru = 1. $$ S = \text(délka) \cdot \text(šířka) = 3 \cdot 1 = 3 \text(jednotka)^2 $$ Jak vidíte, vše perfektně pasovalo.
Nabízí se otázka: jak řešit neurčité integrály a jaký je jejich význam? Řešením takových integrálů je nalezení primitivních funkcí. Tento proces je opakem hledání derivátu. K nalezení primitivní funkce můžete využít naši pomoc při řešení úloh v matematice, nebo si musíte sami přesně zapamatovat vlastnosti integrálů a integrační tabulku nejjednodušších elementárních funkcí. Nález vypadá takto $$ \int f(x) dx = F(x) + C \text(kde) F(x) $ je primitivní funkce $ f(x), C = const $.
Chcete-li vyřešit integrál, musíte integrovat funkci $ f(x) $ vzhledem k proměnné. Pokud je funkce tabulková, pak se odpověď zapíše v příslušném tvaru. Pokud ne, pak se proces redukuje na získání tabulkové funkce z funkce $ f(x) $ složitými matematickými transformacemi. K tomu existují různé metody a vlastnosti, které si probereme níže.
Takže teď udělejme algoritmus, jak řešit integrály pro figuríny?
Algoritmus pro výpočet integrálů
- Najdi určitý integrál nebo ne.
- Pokud není definováno, musíte najít primitivní funkci $ F(x) $ integrandu $ f(x) $ pomocí matematických transformací, které přivedou funkci $ f(x) $ do tabulkového tvaru.
- Je-li definováno, je nutné provést krok 2 a poté dosadit limity $a$ a $b$ do primitivní funkce $F(x)$. Jakým vzorcem to udělat, se dozvíte v článku "Formule Newtona Leibnize".
Příklady řešení
Takže jste se naučili, jak řešit integrály pro figuríny, příklady řešení integrálů byly seřazeny na policích. Naučili se jejich fyzikální a geometrický význam. Metody řešení budou diskutovány v dalších článcích.
Je možné přivést nelineární funkci pod diferenciální znaménko? Ano, pokud je integrand součinem dvou faktorů: jeden faktor je komplexní funkcí nějaké nelineární funkce a druhý faktor je derivace této nelineární funkce. Podívejme se na příklady.
Najděte neurčité integrály.
Příklad 1. ∫(2x + 1)(x 2 + x + 2) 5 dx = ∫(x 2 + x + 2) 5 d (x 2 + x + 2) =(x²+x+2) 6 : 6+C.
Co je to integrand? Práce výkonová funkce z (x 2 + x + 2) a faktoru (2x + 1), který se rovná derivaci základu stupně: (x 2 + x + 2) "= 2x + 1.
To nám umožnilo přinést (2x + 1) pod diferenciální znaménko:
∫u 5 du=u 6 : 6+ C. (vzorec 1). )
Zkouška. (F (x) + C)" = ((x² + x + 2) 6 : 6 + C)′=1/6 6 (x 2 + x + 2) 5 (x 2 + x + 2)" =
\u003d (x 2 + x + 2) 5 (2x + 1) \u003d (2x + 1) (x 2 + x + 2) 5 \u003d f (x).
Příklad 2∫(3x 2 - 2x + 3)(x 3 - x 2 + 3x + 1) 5 dx = ∫(x 3 - x 2 + 3x + 1) 5 d (x 3 - x 2 + 3x + 1) =
=(x³- x²+3x+1) 6 : 6+C
Jak se tento příklad liší od příkladu 1? Nic! Stejná pátá mocnina se základem (x 3 - x 2 + 3x + 1) se vynásobí trinomem (3x 2 - 2x + 3), což je derivace základu stupně: (x 3 - x 2 + 3x + 1) "= 3x 2 - 2x + 3. Tuto základnu stupně jsme přivedli pod diferenciální znaménko, od kterého se hodnota integrandu nezměnila, a pak použili stejný vzorec 1).( Integrály)
Příklad 3
Zde derivace (2x 3 - 3x) dá (6x 2 - 3), a máme
existuje (12x 2 - 6), tedy výraz in 2 krát větší, pak sečteme (2x 3 - 3x) pod znaménkem diferenciálu a dáme faktor před integrál 2 . Aplikujme vzorec 2) ( prostěradlo ).
Co se stane:
Podívejme se na to, že:
![]()

Příklady. Najděte neurčité integrály.
1. ∫(6x+5) 3 dx. jak se rozhodneme? Podívejte se na list a argumentujeme asi takto: integrand je stupeň a máme vzorec pro integrál stupně (vzorec 1) ), ale v něm základ stupně u a také integrační proměnná u
A máme integrační proměnnou X a základ stupně (6x+5). Provedeme změnu integrační proměnné: místo dx napíšeme d (6x+5). co se změnilo? Protože to, co následuje za diferenciálním znaménkem d, je standardně diferencováno,
pak d (6x+5)=6dx, tj. když je proměnná x nahrazena proměnnou (6x + 5), integrand se zvýšil 6krát, takže před znaménko integrálu dáme faktor 1/6. Tyto argumenty můžete napsat takto:
Tento příklad jsme tedy vyřešili zavedením nové proměnné (proměnná x byla nahrazena proměnnou 6x+5). A kde jsi napsal novou proměnnou (6x + 5)? Ve znamení diferenciálu. Proto se tato metoda zavedení nové proměnné často nazývá metoda ( nebo způsobem ) shrnutí(nová proměnná ) pod diferenciálním znaménkem.
Ve druhém příkladu jsme nejprve získali stupeň se záporným exponentem a poté jsme jej uvedli pod diferenciální znaménko (7x-2) a použili integrální vzorec stupně 1) (Integrály ).
Vezměme si příklad řešení 3.
Integrálu předchází koeficient 1/5. Proč? Protože d (5x-2)=5dx, pak při přičtení funkce u=5x-2 pod diferenciální znaménko jsme integrand zvýšili 5krát, proto, aby se hodnota tohoto výrazu nezměnila, bylo nutné dělit 5, tj. vynásobte 1/5. Dále byl použit vzorec 2) (integrály) .
Všechny nejjednodušší integrální vzorce budou vypadat takto:
∫f (x) dx=F (x)+C a musí platit následující rovnost:
(F(x)+C)"=f(x).
Integrační vzorce lze získat invertováním odpovídajících derivačních vzorců.
Opravdu,
Exponent n může být zlomkové. Často musíte najít neurčitý integrál funkce y=√x. Vypočtěte integrál funkce f (x)=√x pomocí vzorce 1) .
Zapišme tento příklad jako vzorec 2) .
![]()
Protože (x+C)"=1, pak ∫dx=x+C.
3) ∫dx=x+C.
Nahradíme-li 1 / x² x -2, vypočítáme integrál 1 / x².
A tuto odpověď byste mohli získat obrácením známého vzorce diferenciace:
Svoji úvahu zapisujeme ve formě vzorce 4).
![]()
Vynásobením obou stran výsledné rovnosti 2 získáme vzorec 5).
![]()
Pojďme najít integrály hlavních goniometrických funkcí se znalostí jejich derivací: (sinx)"=cosx; (cosx)"=-sinx; (tgx)"=1/cos²x; (ctgx)"=-1/sin²x. Získáme integrační vzorce 6) — 9).
6) ∫cosxdx=sinx+C;
7) ∫sinxdx=-cosx+C;
Po prostudování exponenciálních a logaritmických funkcí přidáme několik dalších vzorců.
Základní vlastnosti neurčitého integrálu.
já Derivace neurčitého integrálu se rovná integrandu .
(∫f(x)dx)"=f(x).
II. Diferenciál neurčitého integrálu je roven integrandu.
d∫f (x) dx=f (x) dx.
III. Neurčitý integrál diferenciálu (derivátu) nějaké funkce se rovná součtu této funkce a libovolné konstanty C.
∫dF(x)=F(x)+C nebo ∫F"(x) dx=F(x)+C.
Pozor: ve vlastnostech I, II a III se znaménka diferenciálu a integrálu (integrálu a diferenciálu) navzájem "žerou"!
IV. Konstantní faktor integrandu lze vyjmout ze znaménka integrálu.
∫kf (x) dx=k ∫f (x) dx, Kde k je konstantní hodnota, která se nerovná nule.
proti. Integrál algebraického součtu funkcí se rovná algebraickému součtu integrálů těchto funkcí.
∫(f (x)±g (x)) dx=∫f (x) dx±∫g (x) dx.
VI. Je-li F(x) primitivní pro f(x) a k A b jsou konstantní hodnoty a, k≠0, pak (1/k) F (kx+b) je primitivní pro f (kx+b). Podle pravidla pro výpočet derivace komplexní funkce máme:
Můžeš psát:
Pro každou matematickou akci existuje inverzní akce. Pro působení derivace (hledání derivací funkcí) existuje i inverzní působení – integrace. Pomocí integrace je funkce nalezena (obnovena) její danou derivací nebo diferenciálem. Zavolá se nalezená funkce primitivní.
Definice. Diferencovatelná funkce F(x) se nazývá primitivní pro funkci f(x) v daném intervalu, pokud pro všechny X z tohoto intervalu platí rovnost: F′(x)=f (x).
Příklady. Najděte primitivní funkce pro funkce: 1) f (x)=2x; 2) f(x)=3cos3x.
1) Protože (x²)′=2x, pak podle definice bude funkce F (x)=x² primitivní funkcí pro funkci f (x)=2x.
2) (sin3x)′=3cos3x. Označíme-li f (x)=3cos3x a F (x)=sin3x, pak podle definice primitivní funkce máme: F′(x)=f (x), a proto F (x)=sin3x je primitivní funkce pro f ( x)=3cos3x.
Všimněte si, že a (sin3x +5 )′= 3cos3x a (sin3x -8,2 )′= 3cos3x, ... V obecný pohled lze napsat: (sin3x +C)′= 3cos3x, Kde S je nějaká konstantní hodnota. Tyto příklady hovoří o nejednoznačnosti působení integrace, na rozdíl od působení derivace, kdy jakákoli diferencovatelná funkce má jedinou derivaci.
Definice. Pokud je funkce F(x) je primitivním prvkem funkce f(x) na nějakém intervalu má množina všech primitivních funkcí této funkce tvar:
F(x)+C kde C je libovolné reálné číslo.
Množina všech primitivních funkcí F (x) + C funkce f (x) na uvažovaném intervalu se nazývá neurčitý integrál a značí se symbolem ∫ (celé znaménko). Zapsat: ∫f (x) dx=F (x)+C.
Výraz ∫f(x)dx zní: "integrál ef od x do de x".
f(x)dx je integrand,
f(x) je integrand,
X je integrační proměnná.
F(x) je primitivní pro funkci f(x),
S je nějaká konstantní hodnota.
Nyní lze uvažované příklady zapsat takto:
1) ∫ 2хdx=x²+C. 2) ∫ 3cos3xdx=sin3x+C.
Co znamená znak d?
d- diferenciální znaménko - má dvojí účel: za prvé, toto znaménko odděluje integrand od integrační proměnné; za druhé, vše za tímto znakem je standardně diferencováno a násobeno integrandem.
Příklady. Najít integrály: 3) ∫ 2pxdx; 4) ∫ 2pxdp.
3) Po rozdílové ikoně d náklady XX, A R
∫ 2хрdx=px²+С. Porovnejte s příkladem 1).
Udělejme kontrolu. F′(x)=(px²+C)′=p (x²)′+C′=p 2x=2px=f (x).
4) Po rozdílové ikoně d náklady R. Tedy integrační proměnná R a multiplikátor X by měla být považována za konstantní hodnotu.
∫ 2хрdр=р²х+С. Porovnejte s příklady 1) A 3).
Udělejme kontrolu. F′(p)=(p²x+C)′=x (p²)′+C′=x 2p=2px=f (p).
Strana 1 z 1 1