असमानताओं की व्यवस्थाअज्ञात मात्रा वाले दो या दो से अधिक असमानताओं के किसी भी सेट को कॉल करने की प्रथा है।

इस फॉर्मूलेशन को स्पष्ट रूप से चित्रित किया गया है, उदाहरण के लिए, इस तरह से असमानताओं की प्रणाली:

असमानताओं की प्रणाली को हल करें - एक अज्ञात चर के सभी मूल्यों को खोजने का मतलब है जिसके लिए सिस्टम की प्रत्येक असमानता का एहसास होता है, या यह साबित करने के लिए कि ऐसा कोई नहीं है .

तो, प्रत्येक व्यक्ति के लिए प्रणाली असमानताअज्ञात चर की गणना करें। इसके अलावा, परिणामी मूल्यों में से, केवल उन का चयन करता है जो पहली और दूसरी असमानताओं दोनों के लिए सही हैं। इसलिए, चुने हुए मूल्य को प्रतिस्थापित करते समय, सिस्टम की दोनों असमानताएं सही हो जाती हैं।

आइए कई असमानताओं के समाधान का विश्लेषण करें:

एक को संख्या रेखाओं के दूसरे युग्म के नीचे रखें; मूल्य को शीर्ष पर रखें एक्स, जिसके तहत पहली असमानता ओ ( एक्स> 1) सच हो, और तल पर, मूल्य एक्स, जो दूसरी असमानता का समाधान हैं ( एक्स> 4).

पर डेटा की तुलना करके संख्या रेखा, ध्यान दें कि दोनों के लिए समाधान असमानताओंहोगा एक्स> 4. उत्तर, एक्स> 4.

उदाहरण 2

पहले की गणना असमानताहमें -3 ​​. मिलता है एक्स< -6, или एक्स> 2, दूसरा - एक्स> -8, या एक्स < 8. Затем делаем по аналогии с предыдущим примером. На верхнюю числовую прямую наносим все те значения एक्स, जिसके तहत प्रथम प्रणाली असमानता, और निचली संख्या रेखा पर, वे सभी मान एक्स, जिसके तहत व्यवस्था की दूसरी असमानता का एहसास होता है।

आंकड़ों की तुलना करने पर, हम पाते हैं कि दोनों असमानताओंसभी मूल्यों के लिए लागू किया जाएगा एक्स 2 से 8 तक रखा गया है। मूल्यों के समूह एक्सनिरूपित दोहरी असमानता 2 < एक्स< 8.

उदाहरण 3हमे पता करने दें

रैखिक, वर्ग और . को हल करने के लिए कार्यक्रम भिन्नात्मक असमानताएँयह केवल समस्या का उत्तर नहीं देता है, यह स्पष्टीकरण के साथ एक विस्तृत समाधान देता है, अर्थात। गणित और/या बीजगणित के ज्ञान की जांच करने के लिए हल करने की प्रक्रिया को प्रदर्शित करता है।

इसके अलावा, अगर असमानताओं में से किसी एक को हल करने की प्रक्रिया में हल करना आवश्यक है, उदाहरण के लिए, द्विघात समीकरण, तो इसका विस्तृत समाधान भी प्रदर्शित किया जाता है (इसे स्पॉइलर में शामिल किया जाता है)।

यह कार्यक्रम हाई स्कूल के छात्रों के लिए तैयारी में उपयोगी हो सकता है नियंत्रण कार्यमाता-पिता अपने बच्चों द्वारा असमानताओं के समाधान को नियंत्रित करने के लिए।

यह कार्यक्रम हाई स्कूल के छात्रों के लिए उपयोगी हो सकता है सामान्य शिक्षा स्कूलपरीक्षण और परीक्षा की तैयारी में, परीक्षा से पहले ज्ञान का परीक्षण करते समय, माता-पिता गणित और बीजगणित में कई समस्याओं के समाधान को नियंत्रित करते हैं। या हो सकता है कि आपके लिए ट्यूटर किराए पर लेना या नई पाठ्यपुस्तकें खरीदना बहुत महंगा हो? या आप इसे जल्द से जल्द पूरा करना चाहते हैं? गृहकार्यगणित या बीजगणित? इस मामले में, आप विस्तृत समाधान के साथ हमारे कार्यक्रमों का भी उपयोग कर सकते हैं।

इस तरह, आप अपना खुद का प्रशिक्षण और/या अपने प्रशिक्षण का संचालन कर सकते हैं छोटे भाईया बहनों, जबकि हल किए जा रहे कार्यों के क्षेत्र में शिक्षा का स्तर बढ़ता है।

असमानताओं में प्रवेश करने के नियम

कोई भी लैटिन अक्षर एक चर के रूप में कार्य कर सकता है।
उदाहरण के लिए: \(x, y, z, a, b, c, o, p, q \) आदि।

संख्याओं को पूर्णांक या भिन्न के रूप में दर्ज किया जा सकता है।
इसके अलावा, भिन्नात्मक संख्याओं को न केवल दशमलव के रूप में, बल्कि एक साधारण भिन्न के रूप में भी दर्ज किया जा सकता है।

दशमलव अंशों को दर्ज करने के नियम।
दशमलव भिन्नों में, पूर्णांक से भिन्नात्मक भाग को बिंदु या अल्पविराम द्वारा अलग किया जा सकता है।
उदाहरण के लिए, आप दर्ज कर सकते हैं दशमलवतो: 2.5x - 3.5x ^ 2

साधारण भिन्नों को दर्ज करने के नियम।
केवल एक पूर्ण संख्या भिन्न के अंश, हर और पूर्णांक भाग के रूप में कार्य कर सकती है।

भाजक ऋणात्मक नहीं हो सकता।

एक संख्यात्मक अंश में प्रवेश करते समय, अंश को भाजक से हर से अलग किया जाता है: /
पूरा भागएम्परसेंड द्वारा भिन्न से अलग किया गया: &
इनपुट: 3&1/3 - 5&6/5y +1/7y^2
परिणाम: \(3\frac(1)(3) - 5\frac(6)(5) y + \frac(1)(7)y^2 \)

अभिव्यक्ति दर्ज करते समय कोष्ठक का उपयोग किया जा सकता है। इस मामले में, असमानता को हल करते समय, अभिव्यक्तियों को पहले सरल बनाया जाता है।
उदाहरण के लिए: 5(a+1)^2+2&3/5+a > 0.6(a-2)(a+3)

वांछित असमानता चिह्न चुनें और नीचे के क्षेत्रों में बहुपदों को दर्ज करें।

प्रणाली की पहली असमानता।

पहली असमानता के प्रकार को बदलने के लिए बटन पर क्लिक करें।

> >= < <=

असमानताओं की प्रणाली को हल करें

यह पाया गया कि इस कार्य को हल करने के लिए आवश्यक कुछ लिपियों को लोड नहीं किया गया था, और हो सकता है कि प्रोग्राम काम न करे।
आपके पास एडब्लॉक सक्षम हो सकता है।
इस मामले में, इसे अक्षम करें और पृष्ठ को ताज़ा करें।

आपके ब्राउज़र में जावास्क्रिप्ट अक्षम है।
समाधान के प्रकट होने के लिए जावास्क्रिप्ट सक्षम होना चाहिए।
अपने ब्राउज़र में जावास्क्रिप्ट को कैसे सक्षम करें, इस पर निर्देश यहां दिए गए हैं।

इसलिये बहुत सारे लोग हैं जो समस्या का समाधान करना चाहते हैं, आपका अनुरोध कतार में है।
कुछ सेकंड के बाद, समाधान नीचे दिखाई देगा।
कृपया प्रतीक्षा करें सेकंड...

अगर तुम समाधान में त्रुटि देखी गई, तो आप इसके बारे में फीडबैक फॉर्म में लिख सकते हैं।
मत भूलो इंगित करें कि कौन सा कार्यआप क्या तय करें खेतों में प्रवेश करें.

हमारे खेल, पहेलियाँ, अनुकरणकर्ता:

थोड़ा सिद्धांत।

एक अज्ञात के साथ असमानताओं की प्रणाली। संख्यात्मक स्पैन

आप 7 वीं कक्षा में एक प्रणाली की अवधारणा से परिचित हुए और दो अज्ञात के साथ रैखिक समीकरणों की प्रणालियों को हल करना सीखा। सिस्टम पर आगे चर्चा की जाएगी। रैखिक असमानताएंएक अज्ञात के साथ। असमानताओं की प्रणालियों के समाधान सेट अंतराल (अंतराल, अर्ध-अंतराल, खंड, किरण) का उपयोग करके लिखे जा सकते हैं। आप संख्यात्मक अंतरालों के अंकन के बारे में भी जानेंगे।

यदि असमानताओं \(4x > 2000 \) और \(5x \leq 4000 \) में अज्ञात संख्या x समान है, तो इन असमानताओं को एक साथ माना जाता है और उन्हें असमानताओं की एक प्रणाली बनाने के लिए कहा जाता है: $$ \left\ (\begin(सरणी)(l) 4x > 2000 \\ 5x \leq 4000 \end(array)\right.$$

घुंघराले ब्रेस से पता चलता है कि आपको x के ऐसे मूल्यों को खोजने की जरूरत है, जिसके लिए सिस्टम की दोनों असमानताएं वास्तविक संख्यात्मक असमानताओं में बदल जाती हैं। यह प्रणाली एक अज्ञात के साथ रैखिक असमानताओं की प्रणाली का एक उदाहरण है।

एक अज्ञात के साथ असमानताओं की एक प्रणाली का समाधान अज्ञात का मूल्य है जिस पर प्रणाली की सभी असमानताएं वास्तविक संख्यात्मक असमानताओं में बदल जाती हैं। असमानताओं की एक प्रणाली को हल करने का अर्थ है इस प्रणाली के सभी समाधान खोजना या यह स्थापित करना कि कोई भी नहीं है।

असमानताओं \(x \geq -2 \) और \(x \leq 3 \) को दोहरी असमानता के रूप में लिखा जा सकता है: \(-2 \leq x \leq 3 \)।

एक अज्ञात के साथ असमानताओं की प्रणालियों के समाधान विविध हैं संख्या सेट. इन सेटों के नाम हैं। अतः, वास्तविक अक्ष पर, संख्याओं का समुच्चय x इस प्रकार है कि \(-2 \leq x \leq 3 \) बिंदु -2 और 3 पर समाप्त होने वाले खंड द्वारा दर्शाया गया है।

-2

3

यदि \(a एक खंड है और [a; b] द्वारा दर्शाया गया है

अगर \(एक अंतराल और (ए; बी) द्वारा दर्शाया गया है

संख्याओं के समुच्चय \(x \) असमानताओं को संतुष्ट करते हैं \(a \leq x अर्ध-अंतराल द्वारा और क्रमशः [a; b) और (a; b] द्वारा निरूपित किए जाते हैं।

खंड, अंतराल, अर्ध-अंतराल और किरणें कहलाती हैं संख्यात्मक अंतराल.

इस प्रकार, संख्यात्मक अंतरालों को असमानताओं के रूप में निर्दिष्ट किया जा सकता है।

दो अज्ञात के साथ एक असमानता का समाधान संख्याओं की एक जोड़ी (x; y) है जो इस असमानता को एक वास्तविक संख्यात्मक असमानता में बदल देता है। असमानता को हल करने का अर्थ है उसके सभी समाधानों का समुच्चय खोजना। तो, असमानता का समाधान x > y होगा, उदाहरण के लिए, संख्याओं के जोड़े (5; 3), (-1; -1), क्योंकि \(5 \geq 3 \) और \(-1 \geq - 1\)

असमानताओं का समाधान प्रणाली

आप पहले ही सीख चुके हैं कि एक अज्ञात के साथ रैखिक असमानताओं को कैसे हल किया जाता है। जानिए क्या है असमानताओं की व्यवस्था और व्यवस्था का समाधान। इसलिए, एक अज्ञात के साथ असमानताओं की प्रणालियों को हल करने की प्रक्रिया आपको कोई कठिनाई नहीं देगी।

और फिर भी हम याद करते हैं: असमानताओं की एक प्रणाली को हल करने के लिए, आपको प्रत्येक असमानता को अलग से हल करना होगा, और फिर इन समाधानों के प्रतिच्छेदन का पता लगाना होगा।

उदाहरण के लिए, असमानताओं की मूल प्रणाली को इस रूप में घटा दिया गया था:
$$ \बाएं\(\शुरू(सरणी)(एल) x \geq -2 \\ x \leq 3 \end(सरणी)\दाएं। $$

असमानताओं की इस प्रणाली को हल करने के लिए, वास्तविक अक्ष पर प्रत्येक असमानता के समाधान को चिह्नित करें और उनका प्रतिच्छेदन खोजें:

-2

3

प्रतिच्छेदन खंड है [-2; 3] - यह असमानताओं की मूल प्रणाली का समाधान है।

असमानता समाधानमोड में ऑनलाइन समाधानलगभग किसी भी असमानता ऑनलाइन. गणितीय असमानता ऑनलाइनगणित को हल करने के लिए। जल्दी से खोजें असमानता समाधानमोड में ऑनलाइन. साइट www.site आपको खोजने की अनुमति देती है समाधानलगभग किसी दिए गए बीजगणितीय, त्रिकोणमितीयया पारलौकिक असमानता ऑनलाइन. गणित की लगभग किसी भी शाखा का अध्ययन करते समय विभिन्न चरणोंफैसला करना है असमानता ऑनलाइन. तुरंत उत्तर पाने के लिए, और सबसे महत्वपूर्ण रूप से सटीक उत्तर पाने के लिए, आपको एक ऐसे संसाधन की आवश्यकता है जो आपको ऐसा करने की अनुमति दे। www.site . को धन्यवाद असमानता को ऑनलाइन हल करेंकुछ मिनट लगेंगे। गणितीय हल करते समय www.site का मुख्य लाभ असमानता ऑनलाइन- जारी प्रतिक्रिया की गति और सटीकता है। साइट किसी को भी हल करने में सक्षम है बीजीय असमानताओं ऑनलाइन, त्रिकोणमितीय असमानताएं ऑनलाइन, ट्रान्सेंडैंटल असमानताओं ऑनलाइन, साथ ही असमानताओंमोड में अज्ञात मापदंडों के साथ ऑनलाइन. असमानताओंएक शक्तिशाली गणितीय उपकरण के रूप में कार्य करें समाधानव्यावहारिक कार्य। मदद से गणितीय असमानताएँतथ्यों और संबंधों को व्यक्त करना संभव है जो पहली नज़र में भ्रमित और जटिल लग सकते हैं। अज्ञात मात्रा असमानताओंसमस्या को सूत्रबद्ध करके पाया जा सकता है गणितीयरूप में भाषा असमानताओंतथा तय करनामोड में प्राप्त कार्य ऑनलाइनवेबसाइट www.site पर। कोई बीजगणितीय असमानता, त्रिकोणमितीय असमानताया असमानताओंयुक्त ट्रान्सेंडैंटलआपको आसानी से सुविधाएँ तय करनाऑनलाइन और सही उत्तर प्राप्त करें। प्राकृतिक विज्ञानों का अध्ययन करने पर व्यक्ति को अनिवार्य रूप से आवश्यकता का सामना करना पड़ता है असमानताओं का समाधान. इस मामले में, उत्तर सटीक होना चाहिए और इसे तुरंत मोड में प्राप्त किया जाना चाहिए ऑनलाइन. इसलिए, के लिए गणितीय असमानताओं को ऑनलाइन हल करेंहम साइट www.site की अनुशंसा करते हैं, जो आपके लिए अनिवार्य कैलकुलेटर बन जाएगा बीजीय असमानताओं को ऑनलाइन हल करें, त्रिकोणमितीय असमानताएं ऑनलाइन, साथ ही ट्रान्सेंडैंटल असमानताओं ऑनलाइनया असमानताओंअज्ञात मापदंडों के साथ। विभिन्न के इंट्रावोल समाधान खोजने की व्यावहारिक समस्याओं के लिए गणितीय असमानताएँसंसाधन www.. हल करना असमानता ऑनलाइनस्वयं, प्राप्त उत्तर की जांच करना उपयोगी है ऑनलाइन समाधानअसमानताओंवेबसाइट www.site पर। असमानता को सही ढंग से लिखना और तुरंत प्राप्त करना आवश्यक है ऑनलाइन समाधान, जिसके बाद यह असमानता के अपने समाधान के साथ उत्तर की तुलना करने के लिए ही रहता है। उत्तर की जाँच में एक मिनट से अधिक समय नहीं लगेगा, पर्याप्त असमानता को ऑनलाइन हल करेंऔर उत्तरों की तुलना करें। इससे आपको गलतियों से बचने में मदद मिलेगी फेसलाऔर समय पर उत्तर सही करें असमानताओं को ऑनलाइन हल करनाया बीजगणितीय, त्रिकोणमितीय, उत्कृष्टया असमानताअज्ञात मापदंडों के साथ।

एक असमानता दो संख्याओं या गणितीय अभिव्यक्तियों में से किसी एक से जुड़ी होती है: > (अधिक, सख्त असमानताओं के मामले में),< (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).

असमानता है रैखिकसमीकरण के समान शर्तों के तहत: इसमें केवल पहली डिग्री तक चर होते हैं और इसमें चर के उत्पाद नहीं होते हैं।

रैखिक असमानताओं और रैखिक असमानताओं की प्रणालियों का समाधान उनके ज्यामितीय अर्थ के साथ अटूट रूप से जुड़ा हुआ है: एक रैखिक असमानता का समाधान एक निश्चित आधा-तल है, जिसमें पूरे विमान को एक सीधी रेखा से विभाजित किया जाता है, जिसका समीकरण द्वारा दिया जाता है रैखिक असमानता। यह आधा-तल, और रैखिक असमानताओं की एक प्रणाली के मामले में, कई सीधी रेखाओं से बंधे विमान का एक हिस्सा, ड्राइंग में पाया जाना चाहिए।

बड़ी संख्या में चर के साथ रैखिक असमानताओं की प्रणालियों को हल करने के लिए कई आर्थिक समस्याएं कम हो जाती हैं, विशेष रूप से, रैखिक प्रोग्रामिंग समस्याएं जिसमें किसी फ़ंक्शन का अधिकतम या न्यूनतम पता लगाना आवश्यक होता है।

किसी भी संख्या में अज्ञात के साथ रैखिक असमानताओं को हल करने वाली प्रणाली

आइए पहले हम समतल में रैखिक असमानताओं का विश्लेषण करें। दो चरों वाली एक असमानता पर विचार करें और :

,

चरों के गुणांक कहाँ हैं (कुछ संख्याएँ), मुक्त पद है (कुछ संख्याएँ भी)।

दो अज्ञात के साथ एक असमानता, एक समीकरण की तरह, अनंत संख्या में समाधान हैं। इस असमानता का समाधान इस असमानता को संतुष्ट करने वाली संख्याओं का एक युग्म है। ज्यामितीय रूप से, असमानता के समाधान के समुच्चय को एक सीधी रेखा से घिरे अर्ध-तल के रूप में दर्शाया गया है

,

जिसे हम सीमा रेखा कहेंगे।

चरण 1. रैखिक असमानता के हलों के समुच्चय को आबद्ध करते हुए एक सीधी रेखा की रचना कीजिए

ऐसा करने के लिए, आपको इस रेखा के किन्हीं दो बिंदुओं को जानना होगा। आइए निर्देशांक अक्षों के साथ प्रतिच्छेदन बिंदु खोजें। चौराहा समन्वय एशून्य है (चित्र 1)। इस आंकड़े में कुल्हाड़ियों पर संख्यात्मक मान उदाहरण 1 को संदर्भित करते हैं, जिसका हम इस सैद्धांतिक विषयांतर के तुरंत बाद विश्लेषण करेंगे।

हम एक प्रणाली के रूप में अक्ष के समीकरण के साथ एक सीधी रेखा के समीकरण को हल करके भुज पाते हैं।

आइए अक्ष के साथ प्रतिच्छेदन खोजें:

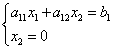
मान को पहले समीकरण में प्रतिस्थापित करने पर, हम प्राप्त करते हैं

कहाँ पे ।

इस प्रकार, हमें बिंदु का भुज ज्ञात हुआ ए .

आइए अक्ष के साथ प्रतिच्छेदन बिंदु के निर्देशांक ज्ञात करें।

एब्सिस्सा पॉइंट बीशून्य के बराबर। आइए समन्वय अक्ष के समीकरण के साथ सीमा रेखा के समीकरण को हल करें:

,

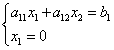
इसलिए बिंदु के निर्देशांक बी: .

चरण 2. एक रेखा खींचिए जो असमानता के समाधानों के समुच्चय को परिबद्ध करती है।बिंदुओं को जानना एतथा बीनिर्देशांक अक्षों के साथ सीमा रेखा का प्रतिच्छेदन, हम यह रेखा खींच सकते हैं। सीधी रेखा (आकृति 1 फिर से) पूरे विमान को इस सीधी रेखा के दाएं और बाएं (ऊपर और नीचे) दो भागों में विभाजित करती है।

चरण 3. निर्धारित करें कि कौन सा अर्ध-तल इस असमानता का समाधान है।ऐसा करने के लिए, हमें निर्देशांक की उत्पत्ति (0; 0) को इस असमानता में प्रतिस्थापित करने की आवश्यकता है। यदि मूल के निर्देशांक असमानता को संतुष्ट करते हैं, तो असमानता का समाधान अर्ध-तल है जिसमें मूल स्थित है। यदि निर्देशांक असमानता को संतुष्ट नहीं करते हैं, तो असमानता का समाधान एक अर्ध-तल है जिसमें मूल शामिल नहीं है। असमानता के समाधान के आधे तल को आधे तल के अंदर सीधी रेखा से स्ट्रोक द्वारा दर्शाया जाएगा, जैसा कि चित्र 1 में दिखाया गया है।

यदि हम रैखिक असमानताओं की प्रणाली को हल करते हैं, तो सिस्टम की प्रत्येक असमानता के लिए प्रत्येक चरण का प्रदर्शन किया जाता है।

उदाहरण 1असमानता को हल करें

समाधान। आइए एक सीधी रेखा खींचते हैं

समीकरण में एक सीधी रेखा को प्रतिस्थापित करने पर, हम प्राप्त करते हैं, और प्रतिस्थापित करने पर, हम प्राप्त करते हैं। इसलिए, अक्षों के साथ प्रतिच्छेदन बिंदुओं के निर्देशांक होंगे ए(3; 0) , बी(0; 2)। इन बिंदुओं के माध्यम से एक सीधी रेखा खींचें (फिर से, चित्र 1)।

हम असमानता के समाधान का आधा तल चुनते हैं। ऐसा करने के लिए, हम शुरुआत (0; 0) के निर्देशांक को असमानता में बदलते हैं:

हम प्राप्त करते हैं, अर्थात, मूल के निर्देशांक इस असमानता को संतुष्ट करते हैं। इसलिए, असमानता का समाधान एक अर्ध-तल है जिसमें मूल, यानी बायां (या निचला) आधा-तल है।

अगर यह असमानता सख्त होती, यानी इसका रूप होता

तो सीमा रेखा के बिंदु समाधान नहीं होंगे, क्योंकि वे असमानता को संतुष्ट नहीं करते हैं।

अब दो अज्ञात के साथ रैखिक असमानताओं की एक प्रणाली पर विचार करें:

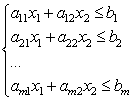
तल पर इस प्रणाली की प्रत्येक असमानता एक अर्ध-तल को परिभाषित करती है। रैखिक असमानताओं की एक प्रणाली को सुसंगत कहा जाता है यदि इसका कम से कम एक समाधान होता है, और यदि इसका कोई समाधान नहीं होता है तो असंगत होता है। रैखिक असमानताओं की एक प्रणाली का समाधान संख्याओं की कोई भी जोड़ी () है जो इस प्रणाली की सभी असमानताओं को संतुष्ट करता है।

ज्यामितीय रूप से, रैखिक असमानताओं की एक प्रणाली का समाधान उन बिंदुओं का समूह है जो सिस्टम की सभी असमानताओं को संतुष्ट करते हैं, जो कि परिणामी अर्ध-तलों का सामान्य भाग है। इसलिए, ज्यामितीय रूप से, सामान्य मामले में, समाधान को एक निश्चित बहुभुज के रूप में चित्रित किया जा सकता है, एक विशेष मामले में, यह एक रेखा, एक खंड और एक बिंदु भी हो सकता है। यदि रैखिक असमानताओं की प्रणाली असंगत है, तो तल पर एक भी बिंदु नहीं है जो प्रणाली की सभी असमानताओं को संतुष्ट करता है।

उदाहरण 2

समाधान। इसलिए, असमानताओं की इस प्रणाली के समाधानों का बहुभुज खोजना आवश्यक है। आइए पहली असमानता के लिए एक सीमा रेखा का निर्माण करें, यानी एक रेखा, और दूसरी असमानता के लिए एक सीमा रेखा, यानी एक रेखा।

हम यह कदम दर कदम करते हैं, जैसा कि सैद्धांतिक संदर्भ में दिखाया गया था और उदाहरण 1 में, खासकर जब से उदाहरण 1 में असमानता के लिए एक सीमा रेखा बनाई गई थी, जो इस प्रणाली में पहली है।

इस प्रणाली की असमानताओं के अनुरूप समाधान अर्ध-तलों को चित्र 2 में अंदर की ओर छायांकित किया गया है। अर्ध-तलों के विलयन का उभयनिष्ठ भाग एक खुला कोण है एबीसी. इसका मतलब है कि खुले कोण को बनाने वाले समतल में बिंदुओं का समूह एबीसी, प्रणाली की पहली और दूसरी दोनों असमानताओं का समाधान है, यानी दो रैखिक असमानताओं की प्रणाली का समाधान है। दूसरे शब्दों में, इस समुच्चय के किसी भी बिंदु के निर्देशांक निकाय की दोनों असमानताओं को संतुष्ट करते हैं।

उदाहरण 3रैखिक असमानताओं की एक प्रणाली को हल करें

समाधान। आइए हम प्रणाली की असमानताओं के अनुरूप सीमा रेखाएँ बनाते हैं। हम प्रत्येक असमानता के लिए सैद्धांतिक पृष्ठभूमि में दिए गए चरणों का पालन करके ऐसा करते हैं। अब हम प्रत्येक असमानता के लिए हल के अर्ध-तलों को परिभाषित करते हैं (चित्र 3)।

दिए गए सिस्टम की असमानताओं के अनुरूप समाधान अर्ध-तलों को अंदर की ओर छायांकित किया जाता है। समाधान के अर्ध-तलों का प्रतिच्छेदन दर्शाया गया है, जैसा कि चित्र में दिखाया गया है, चतुर्भुज के रूप में एबीसीई. हमने पाया है कि दो चरों वाली रैखिक असमानताओं के निकाय का हल बहुभुज एक चतुर्भुज होता है एबीसीई .

दो अज्ञात के साथ रैखिक असमानताओं की प्रणालियों के बारे में ऊपर वर्णित सब कुछ अज्ञात की किसी भी संख्या के साथ असमानताओं की एक प्रणाली पर भी लागू होता है, केवल अंतर के साथ असमानता का समाधान एनअज्ञात समग्रता होगी एनसंख्याएँ () सभी असमानताओं को संतुष्ट करती हैं, और सीमा रेखा के बजाय एक सीमा हाइपरप्लेन होगी एन-आयामी अंतरिक्ष। समाधान हाइपरप्लेन से घिरा एक समाधान पॉलीहेड्रॉन (सिम्पलेक्स) होगा।

यह भी देखें एक रैखिक प्रोग्रामिंग समस्या को ग्राफिक रूप से हल करना, रैखिक प्रोग्रामिंग समस्याओं का कैननिकल रूप

इस तरह की समस्या के लिए बाधाओं की प्रणाली में दो चर में असमानताएं होती हैं:
और उद्देश्य समारोह का रूप है एफ = सी 1 एक्स + सी 2 आप, जिसे अधिकतम किया जाना है।

आइए इस प्रश्न का उत्तर दें: संख्याओं के कौन से जोड़े ( एक्स; आप) असमानताओं की प्रणाली के समाधान हैं, अर्थात्, क्या वे प्रत्येक असमानता को एक साथ संतुष्ट करते हैं? दूसरे शब्दों में, किसी सिस्टम को आलेखीय रूप से हल करने का क्या अर्थ है?
पहले आपको यह समझने की जरूरत है कि दो अज्ञात के साथ एक रैखिक असमानता का समाधान क्या है।
दो अज्ञात के साथ एक रैखिक असमानता को हल करने का अर्थ है अज्ञात के मूल्यों के सभी जोड़े निर्धारित करना जिसके लिए असमानता संतुष्ट है।
उदाहरण के लिए, असमानता 3 एक्स – 5आप 42 जोड़े को संतुष्ट करें ( एक्स , आप) : (100, 2); (3, -10), आदि। समस्या ऐसे सभी जोड़ों को खोजने की है।
दो असमानताओं पर विचार करें: कुल्हाड़ी + द्वारा≤ सी, कुल्हाड़ी + द्वारा≥ सी. सीधा कुल्हाड़ी + द्वारा = सीविमान को दो अर्ध-तलों में विभाजित करता है ताकि उनमें से एक के बिंदुओं के निर्देशांक असमानता को संतुष्ट करें कुल्हाड़ी + द्वारा >सी, और अन्य असमानता कुल्हाड़ी + +द्वारा <सी.
वास्तव में, निर्देशांक के साथ एक बिंदु लें एक्स = एक्स 0; फिर एक बिंदु एक सीधी रेखा पर पड़ा हुआ है और एक भुज है एक्स 0 , एक कोटि है

निश्चित होने दें एक<0, बी>0, सी>0. एब्सिस्सा के साथ सभी बिंदु एक्स 0 ऊपर पी(जैसे डॉट एम), पास होना वाई एम>आप 0 , और बिंदु के नीचे के सभी बिंदु पी, भुज के साथ एक्स 0, है Y n<आप 0. क्यों कि एक्स 0 एक मनमाना बिंदु है, तो रेखा के एक तरफ हमेशा ऐसे बिंदु होंगे जिनके लिए कुल्हाड़ी+ द्वारा > सी, एक अर्ध-तल बनाते हुए, और दूसरी ओर, ऐसे बिंदु जिनके लिए कुल्हाड़ी + द्वारा< सी.

चित्र 1

अर्ध-तल में असमानता का चिन्ह संख्याओं पर निर्भर करता है एक, बी , सी.
इसका तात्पर्य दो चरों में रैखिक असमानताओं की प्रणालियों के चित्रमय समाधान के लिए निम्नलिखित विधि से है। सिस्टम को हल करने के लिए, आपको चाहिए:

1. प्रत्येक असमानता के लिए, दी गई असमानता के अनुरूप समीकरण लिखिए।
2. ऐसी रेखाएँ बनाएँ जो समीकरणों द्वारा दिए गए फलनों के ग्राफ़ हों।
3. प्रत्येक सीधी रेखा के लिए, अर्ध-तल निर्धारित करें, जो असमानता द्वारा दिया गया है। ऐसा करने के लिए, एक मनमाना बिंदु लें जो एक सीधी रेखा पर नहीं है, इसके निर्देशांक को असमानता में बदलें। यदि असमानता सत्य है, तो चुना हुआ बिंदु वाला आधा तल मूल असमानता का समाधान है। यदि असमानता असत्य है, तो रेखा के दूसरी ओर अर्ध-तल इस असमानता के समाधान का समुच्चय है।
4. असमानताओं की एक प्रणाली को हल करने के लिए, सभी आधे विमानों के चौराहे के क्षेत्र को खोजना आवश्यक है जो सिस्टम में प्रत्येक असमानता का समाधान है।

यह क्षेत्र खाली हो सकता है, तो असमानताओं की व्यवस्था का कोई समाधान नहीं है, यह असंगत है। अन्यथा, सिस्टम को सुसंगत कहा जाता है।
समाधान एक परिमित संख्या और अनंत समुच्चय हो सकते हैं। क्षेत्रफल एक बंद बहुभुज हो सकता है या यह असीमित हो सकता है।

आइए तीन प्रासंगिक उदाहरण देखें।

उदाहरण 1. सिस्टम को ग्राफिक रूप से हल करें:
एक्स + वाई- 1 ≤ 0;
–2एक्स- 2आप + 5 ≤ 0.

• समीकरणों पर विचार करें x+y–1=0 तथा –2x–2y+5=0 असमानताओं के अनुरूप;
• आइए हम इन समीकरणों द्वारा दी गई सीधी रेखाओं की रचना करें।

चित्र 2

आइए हम असमानताओं द्वारा दिए गए अर्ध-तलों को परिभाषित करें। एक मनमाना बिंदु लीजिए, मान लीजिए (0; 0)। विचार करना एक्स+ y- 1 0, हम बिंदु (0; 0) को प्रतिस्थापित करते हैं: 0 + 0 - 1 ≤ 0। इसलिए, अर्ध-तल में जहां बिंदु (0; 0) स्थित है, एक्स + आप – 1 0, अर्थात्। सीधी रेखा के नीचे स्थित आधा तल पहली असमानता का समाधान है। इस बिंदु (0; 0) को दूसरे बिंदु में प्रतिस्थापित करने पर, हम प्राप्त करते हैं: -2 ∙ 0 - 2 0 + 5 ≤ 0, अर्थात। अर्ध-तल में जहां बिंदु (0; 0) स्थित है, -2 एक्स – 2आप+5≥ 0, और हमसे पूछा गया कि -2 . कहाँ एक्स – 2आप+ 5 0, इसलिए, एक और अर्ध-तल में - सीधी रेखा के ऊपर वाले में।
इन दो अर्ध-तलों का प्रतिच्छेदन ज्ञात कीजिए। रेखाएँ समानांतर हैं, इसलिए समतल कहीं भी प्रतिच्छेद नहीं करते हैं, जिसका अर्थ है कि इन असमानताओं की प्रणाली का कोई समाधान नहीं है, यह असंगत है।

उदाहरण 2. असमानताओं की प्रणाली के लिए ग्राफिक रूप से समाधान खोजें:

चित्र तीन
1. असमानताओं के संगत समीकरण लिखिए और सीधी रेखाएँ बनाइए।
एक्स + 2आप– 2 = 0

एक्स	2	0
आप	0	1

आप – एक्स – 1 = 0

एक्स	0	2
आप	1	3

आप + 2 = 0;
आप = –2.
2. बिंदु (0; 0) को चुनने के बाद, हम अर्ध-तलों में असमानताओं के संकेत निर्धारित करते हैं:
0 + 2 0 - 2 ≤ 0, अर्थात्। एक्स + 2आप- 2 0 सीधी रेखा के नीचे आधे तल में;
0 - 0 - 1 0, अर्थात्। आप –एक्स- 1 0 सीधी रेखा के नीचे आधे तल में;
0 + 2 =2 0, अर्थात्। आप+ 2 0 रेखा के ऊपर अर्ध-तल में।
3. इन तीन अर्ध-तलों का प्रतिच्छेदन एक ऐसा क्षेत्रफल होगा जो एक त्रिभुज है। संबंधित रेखाओं के प्रतिच्छेदन बिंदुओं के रूप में क्षेत्र के शीर्षों को खोजना कठिन नहीं है


इस तरह, लेकिन(–3; –2), पर(0; 1), से(6; –2).

आइए एक और उदाहरण पर विचार करें, जिसमें सिस्टम के समाधान का परिणामी डोमेन सीमित नहीं है।