एक अनिश्चित अभिन्न (एंटीडेरिवेटिव्स या "एंटी-डेरिवेटिव्स" का एक सेट) खोजने का अर्थ है इस फ़ंक्शन के ज्ञात व्युत्पन्न से फ़ंक्शन को पुनर्स्थापित करना। एंटीडेरिवेटिव्स का बहाल सेट एफ(एक्स) + से समारोह के लिए एफ(एक्स) एकीकरण स्थिरांक को ध्यान में रखता है सी. एक भौतिक बिंदु (व्युत्पन्न) की गति के अनुसार, इस बिंदु (मूल) की गति के नियम को बहाल किया जा सकता है; किसी बिंदु की गति के त्वरण के अनुसार - उसकी गति और गति का नियम। जैसा कि आप देख सकते हैं, भौतिकी से शर्लक होम्स की गतिविधि के लिए एकीकरण एक विस्तृत क्षेत्र है। हां, और अर्थव्यवस्था में, कई अवधारणाओं को कार्यों और उनके डेरिवेटिव के माध्यम से दर्शाया जाता है, और इसलिए, उदाहरण के लिए, यह संभव है एक निश्चित क्षणसमय (व्युत्पन्न) संबंधित समय पर उत्पादित उत्पादों की मात्रा को बहाल करने के लिए।

अनिश्चितकालीन समाकलन ज्ञात करने के लिए काफी कम संख्या में मूल समाकलन सूत्रों की आवश्यकता होती है। लेकिन इसे खोजने की प्रक्रिया केवल इन सूत्रों को लागू करने की तुलना में कहीं अधिक कठिन है। सभी जटिलताएं एकीकरण से संबंधित नहीं हैं, बल्कि अभिन्न अभिव्यक्ति को ऐसे रूप में लाने के लिए हैं जो ऊपर वर्णित मूल सूत्रों का उपयोग करके अनिश्चितकालीन अभिन्न को खोजना संभव बनाता है। इसका मतलब है कि एकीकरण का अभ्यास शुरू करने के लिए, आपको प्राप्त परिणामों को सक्रिय करने की आवश्यकता है उच्च विद्यालयअभिव्यक्ति परिवर्तन कौशल।

हम का उपयोग करके समाकलन ज्ञात करना सीखेंगे गुण और अनिश्चितकालीन अभिन्न की तालिकाइस विषय की बुनियादी अवधारणाओं के बारे में पाठ से (एक नई विंडो में खुलता है)।

समाकल ज्ञात करने की कई विधियाँ हैं, जिनमें से परिवर्तनीय प्रतिस्थापन विधितथा भागों द्वारा एकीकरण की विधि- उच्च गणित सफलतापूर्वक उत्तीर्ण करने वाले प्रत्येक व्यक्ति के लिए एक अनिवार्य सज्जन सेट। हालांकि, अनिश्चित अभिन्न के गुणों पर निम्नलिखित दो प्रमेयों के आधार पर विस्तार विधि का उपयोग करके एकीकरण सीखना शुरू करना अधिक उपयोगी और सुखद है, जिसे हम यहां सुविधा के लिए दोहराएंगे।

प्रमेय 3.समाकलन में अचर गुणनखंड को अनिश्चित समाकल के चिह्न से निकाला जा सकता है, अर्थात्।

प्रमेय 4.फलनों की एक सीमित संख्या के बीजीय योग का अनिश्चित समाकल इन फलनों के अनिश्चित समाकलों के बीजगणितीय योग के बराबर होता है, अर्थात्।

(2)

इसके अलावा, निम्नलिखित नियम एकीकरण में उपयोगी हो सकता है: यदि समाकलन के व्यंजक में एक स्थिर गुणनखंड होता है, तो प्रतिअवकलन के व्यंजक को अचर गुणनखंड के व्युत्क्रम से गुणा किया जाता है, अर्थात्

(3)

चूंकि यह पाठ एकीकरण समस्याओं को हल करने के लिए एक परिचय है, इसलिए दो चीजों पर ध्यान देना महत्वपूर्ण है जो या तो पहले से ही हैं आरंभिक चरण, या थोड़ी देर बाद आपको आश्चर्य हो सकता है। आश्चर्य इस तथ्य के कारण है कि एकीकरण भेदभाव का उलटा संचालन है और अनिश्चितकालीन अभिन्न को "एंटी-डेरिवेटिव" कहा जा सकता है।

पहली बात जो एकीकृत करते समय आश्चर्यचकित नहीं होनी चाहिए।इंटीग्रल की तालिका में ऐसे सूत्र हैं जिनका व्युत्पन्न तालिका के सूत्रों में कोई एनालॉग नहीं है . ये निम्नलिखित सूत्र हैं:

हालाँकि, कोई यह सत्यापित कर सकता है कि इन सूत्रों के दायीं ओर के व्यंजकों का अवकलज संगत समाकलों से मेल खाता है।

दूसरी बात एकीकृत करते समय आश्चर्यचकित न हों. यद्यपि किसी भी प्राथमिक फलन का अवकलज भी एक प्राथमिक फलन है, कुछ प्राथमिक फलनों के अनिश्चित समाकल अब प्राथमिक फलन नहीं रह गए हैं . ऐसे अभिन्न के उदाहरण हैं:

एक एकीकरण तकनीक विकसित करने के लिए निम्नलिखित कौशल उपयोगी होंगे: अंशों को कम करना, एक बहुपद को अंश में एक मोनोमियल द्वारा हर में एक मोनोमियल द्वारा विभाजित करना (अनिश्चित अभिन्न का योग प्राप्त करने के लिए), जड़ों को एक शक्ति में परिवर्तित करना, एक मोनोमियल को गुणा करके एक बहुपद, एक शक्ति को ऊपर उठाना। इंटीग्रैंड को बदलने के लिए इन कौशलों की आवश्यकता होती है, जिसके परिणामस्वरूप इंटीग्रल की तालिका में मौजूद इंटीग्रल का योग होना चाहिए।

अनिश्चित समाकलों को एक साथ ढूँढना

उदाहरण 1अनिश्चितकालीन अभिन्न का पता लगाएं

.

समाधान। हम समाकलन के हर में एक बहुपद देखते हैं जिसमें x का वर्ग है। यह लगभग एक निश्चित संकेत है कि तालिका अभिन्न 21 (परिणाम के चाप स्पर्शरेखा के साथ) को लागू किया जा सकता है। हम भाजक से गुणनखंड-दो निकालते हैं (अभिन्न का ऐसा गुण होता है - समाकलन चिह्न से एक अचर गुणनखंड निकाला जा सकता है, इसे ऊपर प्रमेय 3 के रूप में वर्णित किया गया था)। इन सबका परिणाम :

अब हर वर्गों का योग है, जिसका अर्थ है कि हम उल्लिखित तालिका अभिन्न को लागू कर सकते हैं। अंत में हमें उत्तर मिलता है:

.

उदाहरण 2अनिश्चितकालीन अभिन्न का पता लगाएं

समाधान। हम फिर से प्रमेय 3 लागू करते हैं - अभिन्न का गुण, जिसके आधार पर स्थिर कारक को अभिन्न चिह्न से निकाला जा सकता है:

हम समाकलन की तालिका (डिग्री में चर) से सूत्र 7 को समाकलन पर लागू करते हैं:

.

हम परिणामी भिन्नों को कम करते हैं और हमारे पास अंतिम उत्तर होता है:

उदाहरण 3अनिश्चितकालीन अभिन्न का पता लगाएं

समाधान। गुणों पर पहले प्रमेय 4 और फिर प्रमेय 3 को लागू करने पर, हम इस समाकल को तीन समाकलों के योग के रूप में पाते हैं:

प्राप्त सभी तीन समाकल सारणीबद्ध हैं। हम के लिए समाकलकों की तालिका से सूत्र (7) का उपयोग करते हैं एन = 1/2, एन= 2 और एन= 1/5, और फिर

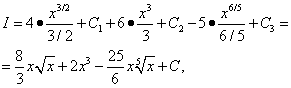
सभी तीन मनमाना स्थिरांक को जोड़ती है जो तीन अभिन्नों को खोजने के दौरान पेश किए गए थे। इसलिए, समान स्थितियों में, एकीकरण का केवल एक मनमाना स्थिरांक (स्थिर) पेश किया जाना चाहिए।

उदाहरण 4अनिश्चितकालीन अभिन्न का पता लगाएं

समाधान। जब समाकलन के हर में एकपदी होती है, तो हम अंश को हर पद से पद से विभाजित कर सकते हैं। मूल समाकलन दो समाकलनों के योग में बदल गया:

.

टेबल इंटीग्रल को लागू करने के लिए, हम जड़ों को घात में बदलते हैं और यहाँ अंतिम उत्तर है:

हम अनिश्चितकालीन समाकलों को एक साथ खोजना जारी रखते हैं

उदाहरण 7अनिश्चितकालीन अभिन्न का पता लगाएं

समाधान। यदि हम द्विपद का वर्ग करके समाकलन को रूपांतरित करते हैं और अंश को हर पद से विभाजित करते हैं, तो मूल समाकल तीन समाकलों का योग बन जाता है।

गणना विधियों का अवलोकन प्रस्तुत किया गया है अनिश्चित समाकलन. एकीकरण के मुख्य तरीकों पर विचार किया जाता है, जिसमें योग और अंतर का एकीकरण, स्थिरांक को अभिन्न चिह्न से बाहर निकालना, चर को बदलना और भागों द्वारा एकीकृत करना शामिल है। यह भी माना जाता है विशेष तरीकेऔर भिन्नों, मूलों, त्रिकोणमितीय और घातांकीय कार्यों को एकीकृत करने की तकनीकें।

एंटिडेरिवेटिव और अनिश्चितकालीन अभिन्न

फलन f(x) का प्रतिअवकलन F(x) एक ऐसा फलन है जिसका अवकलज f(x) के बराबर है:
एफ′(एक्स) = एफ(एक्स), एक्स ∈,
कहाँ पे Δ - वह अंतराल जिस पर यह समीकरण संतुष्ट होता है।

सभी प्रतिपदार्थों के समुच्चय को अनिश्चित समाकलन कहा जाता है:
,
जहाँ C, x से अचर स्वतंत्र है।

मूल सूत्र और एकीकरण के तरीके

इंटीग्रल की तालिका

अनिश्चित समाकलों की गणना का अंतिम लक्ष्य, रूपांतरणों के माध्यम से, दिए गए समाकल को सरल या सारणीबद्ध समाकलों वाले व्यंजक में लाना है।
इंटीग्रल की तालिका देखें >>>

योग (अंतर) एकीकरण नियम

अभिन्न चिह्न से स्थिरांक निकालना

मान लीजिए कि c, x से एक अचर स्वतंत्र है। तब इसे अभिन्न चिन्ह से निकाला जा सकता है:

परिवर्तनीय प्रतिस्थापन

मान लीजिए x एक चर t , x = (t) का एक फलन है, तो
.
या इसके विपरीत, t = (x) ,
.

चर के परिवर्तन की मदद से, आप न केवल सरल इंटीग्रल की गणना कर सकते हैं, बल्कि अधिक जटिल लोगों की गणना को भी सरल बना सकते हैं।

भागों द्वारा एकीकरण का नियम

भिन्नों का एकीकरण (तर्कसंगत कार्य)

आइए एक संकेतन का परिचय दें। मान लीजिए P k (x), Q m (x), R n (x) चर x के संबंध में क्रमशः k, m, n डिग्री वाले बहुपदों को दर्शाता है।

बहुपद (तथाकथित तर्कसंगत कार्य) के एक अंश से मिलकर एक अभिन्न पर विचार करें:

यदि k n, तो सबसे पहले आपको भिन्न के पूर्णांक भाग का चयन करना होगा:
.
बहुपद S k-n (x) का समाकल समाकलन की तालिका से परिकलित किया जाता है।

अभिन्न अवशेष:
, जहां एम< n .
इसकी गणना करने के लिए, समाकलन को साधारण भिन्नों में विघटित किया जाना चाहिए।

ऐसा करने के लिए, आपको समीकरण की जड़ों को खोजने की जरूरत है:
क्यू एन (एक्स) = 0।
प्राप्त मूलों का उपयोग करते हुए, आपको हर को गुणनखंडों के गुणनफल के रूप में निरूपित करने की आवश्यकता है:
क्यू एन (एक्स) = एस (एक्स-ए) एन ए (एक्स-बी) एन बी ... (एक्स 2 +एक्स+एफ) एन ई (एक्स 2 +जीएक्स+के) एन जी ....
यहाँ s x n , x 2 + ex + f > 0 , x 2 + gx + k > 0 , ... के लिए गुणांक है।

उसके बाद, भिन्न को सरलतम में विघटित करें:

समाकलन करने पर हमें सरल समाकलों से युक्त व्यंजक प्राप्त होता है।
फॉर्म के इंटीग्रल

सारणीबद्ध प्रतिस्थापन t = x - a में घटाया जाता है।

अभिन्न पर विचार करें:

आइए अंश को रूपांतरित करें:
.
समाकलन में प्रतिस्थापित करने पर, हमें एक व्यंजक प्राप्त होता है जिसमें दो समाकलन शामिल होते हैं:
,
.
सबसे पहले, प्रतिस्थापन t \u003d x 2 + ex + f को तालिका में घटाया जाता है।
दूसरा, कमी सूत्र के अनुसार:

अभिन्न में कम हो गया है

हम इसके हर को वर्गों के योग में लाते हैं:
.
फिर प्रतिस्थापन द्वारा, अभिन्न

तालिका में भी दिया गया है।

अपरिमेय कार्यों का एकीकरण

आइए एक संकेतन का परिचय दें। मान लीजिए R(u 1 , u 2 , ... , u n ) चर u 1 , u 2 , ... , u n के एक परिमेय फलन को निरूपित करता है। वह है
,
जहाँ P, Q, u 1 , u 2 , ... , u n चरों वाले बहुपद हैं।

भिन्नात्मक रैखिक अपरिमेयता

फॉर्म के इंटीग्रल पर विचार करें:
,
कहाँ पे - परिमेय संख्या, m 1 , n 1 , ..., m s , n s पूर्णांक हैं।
मान लीजिए n संख्याओं r 1 , ..., r s का उभयनिष्ठ हर है।
तब समाकलन को प्रतिस्थापन द्वारा परिमेय कार्यों के समाकल में घटाया जाता है:
.

अंतर द्विपद से समाकलन

अभिन्न पर विचार करें:
,
जहाँ m, n, p परिमेय संख्याएँ हैं, a, b वास्तविक संख्याएँ हैं।
इस तरह के इंटीग्रल तीन मामलों में तर्कसंगत कार्यों के इंटीग्रल को कम करते हैं।

1) यदि p एक पूर्णांक है। प्रतिस्थापन x = t N, जहाँ N भिन्न m और n का उभयनिष्ठ हर है।
2) यदि एक पूर्णांक है। प्रतिस्थापन a x n + b = t M, जहाँ M, p का हर है।
3) यदि एक पूर्णांक है। प्रतिस्थापन a + b x - n = t M, जहाँ M, p का हर है।

यदि तीन संख्याओं में से कोई भी पूर्णांक नहीं है, तो चेबीशेव के प्रमेय द्वारा इस रूप के समाकलकों को प्राथमिक कार्यों के परिमित संयोजन द्वारा व्यक्त नहीं किया जा सकता है।

कुछ मामलों में, पहले m और p के अधिक सुविधाजनक मानों के लिए इंटीग्रल को कम करना उपयोगी हो सकता है। यह कास्ट सूत्रों का उपयोग करके किया जा सकता है:
;
.

एक वर्ग त्रिपद के वर्गमूल वाले समाकलन

यहां हम फॉर्म के इंटीग्रल पर विचार करते हैं:
,

यूलर प्रतिस्थापन

इस तरह के इंटीग्रल को तीन यूलर प्रतिस्थापनों में से एक के तर्कसंगत कार्यों के इंटीग्रल में घटाया जा सकता है:
, a > 0 के लिए;
, सी > 0 के लिए;
, जहां x 1 समीकरण a x 2 + b x + c = 0 का मूल है। यदि इस समीकरण की वास्तविक जड़ें हैं।

त्रिकोणमितीय और अतिपरवलयिक प्रतिस्थापन

प्रत्यक्ष तरीके

ज्यादातर मामलों में, यूलर प्रतिस्थापन के परिणामस्वरूप प्रत्यक्ष विधियों की तुलना में लंबी गणना होती है। प्रत्यक्ष विधियों का उपयोग करते हुए, समाकलन को निम्न प्रकारों में से एक में घटाया जाता है।

मैं अंकित करता हुँ

फॉर्म का इंटीग्रल:
,
जहाँ P n (x) घात n का एक बहुपद है।

इस तरह के इंटीग्रल पहचान का उपयोग करते हुए अनिश्चित गुणांक की विधि द्वारा पाए जाते हैं:

इस समीकरण को अलग करने और बाएँ और दाएँ पक्षों को समान करने पर, हम गुणांक A i पाते हैं।

द्वितीय प्रकार

फॉर्म का इंटीग्रल:
,
जहाँ P m (x) घात m का एक बहुपद है।

प्रतिस्थापन टी = (एक्स - α) -1यह अभिन्न पिछले प्रकार के लिए कम हो गया है। यदि m n, तो भिन्न का एक पूर्णांक भाग होना चाहिए।

तृतीय प्रकार

तीसरा और सबसे कठिन प्रकार:
.

यहां आपको एक प्रतिस्थापन करने की आवश्यकता है:
.
तब इंटीग्रल फॉर्म लेगा:
.
इसके अलावा, स्थिरांक α, β को इस तरह चुना जाना चाहिए कि t पर गुणांक गायब हो जाएं:
बी = 0, बी 1 = 0।
फिर इंटीग्रल दो प्रकार के इंटीग्रल के योग में विघटित हो जाता है:
;
,
जो क्रमशः प्रतिस्थापन द्वारा एकीकृत होते हैं:
जेड 2 \u003d ए 1 टी 2 + सी 1;
वाई 2 \u003d ए 1 + सी 1 टी -2।

सामान्य मामला

अनुवांशिक (त्रिकोणमितीय और घातीय) कार्यों का एकीकरण

हम पहले ही नोट कर लेते हैं कि वे विधियाँ जो त्रिकोणमितीय फलनों पर लागू होती हैं, अतिपरवलयिक फलनों पर भी लागू होती हैं। इस कारण से, हम अतिपरवलयिक फलनों के एकीकरण पर अलग से विचार नहीं करेंगे।

cos x और sin x . के परिमेय त्रिकोणमितीय फलनों का एकीकरण

फॉर्म के त्रिकोणमितीय कार्यों के इंटीग्रल पर विचार करें:
,
जहाँ R एक परिमेय फलन है। इसमें स्पर्शरेखा और कोटंगेंट भी शामिल हो सकते हैं, जिन्हें साइन और कोसाइन के माध्यम से परिवर्तित किया जाना चाहिए।

ऐसे कार्यों को एकीकृत करते समय, तीन नियमों को ध्यान में रखना उपयोगी होता है:
1) अगर आर ( cosx, sinx)मात्राओं में से एक के सामने साइन परिवर्तन से -1 से गुणा किया जाता है क्योंकि xया पाप x, तो उनमें से दूसरे को t से निरूपित करना उपयोगी है।
2) अगर आर ( cosx, sinx)पहले एक ही समय में संकेत बदलने से नहीं बदलता है क्योंकि xतथा पाप x, तो यह डालना उपयोगी है तन एक्स = टीया सीटीजी एक्स = टी.
3) सभी स्थितियों में प्रतिस्थापन एक परिमेय भिन्न के समाकल की ओर ले जाता है। दुर्भाग्य से, यह प्रतिस्थापन पिछले वाले की तुलना में लंबी गणनाओं में परिणत होता है, यदि लागू हो।

cos x और sin x . के घात फलन का गुणनफल

फॉर्म के इंटीग्रल पर विचार करें:

यदि m और n परिमेय संख्याएँ हैं, तो क्रमचयों में से एक t = पाप xया टी = क्योंकि xसमाकल अवकल द्विपद के समाकल में कम हो जाता है।

यदि m और n पूर्णांक हैं, तो पूर्णांकों की गणना भागों द्वारा एकीकृत करके की जाती है। इसके परिणामस्वरूप निम्नलिखित कमी सूत्र प्राप्त होते हैं:

;
;
;
.

भागों द्वारा एकीकरण

यूलर सूत्र का अनुप्रयोग

यदि कार्यों में से किसी एक के संबंध में इंटीग्रैंड रैखिक है
क्योंकि कुल्हाड़ीया सिनैक्स, तो यूलर सूत्र लागू करना सुविधाजनक है:
ई आईएक्स = cos ax + isin ax(जहां मैं 2 = - 1 ),
इस फ़ंक्शन को के साथ बदलना ईआईएएक्सऔर वास्तविक को हाइलाइट करना (बदलते समय क्योंकि कुल्हाड़ी) या काल्पनिक भाग (बदलते समय सिनैक्स) परिणाम से।

सन्दर्भ:
एन.एम. गुंथर, आर.ओ. कुज़मिन, उच्च गणित में समस्याओं का संग्रह, लैन, 2003।

"गणित" नामक विज्ञान में समाकलन को हल करने की प्रक्रिया को समाकलन कहा जाता है। एकीकरण की मदद से, आप कुछ भौतिक मात्राएँ पा सकते हैं: क्षेत्रफल, आयतन, पिंडों का द्रव्यमान, और बहुत कुछ।

इंटीग्रल अनिश्चित और निश्चित हैं। एक निश्चित समाकल के रूप पर विचार करें और उसके भौतिक अर्थ को समझने का प्रयास करें। यह इस प्रकार दिखाई देता है: $$ \int ^a _b f(x) dx $$। विशेष फ़ीचरएक अनिश्चित समाकल का एक निश्चित समाकल लिखना जिसमें समाकलन की सीमाएँ a और b हैं। अब हम यह पता लगाएंगे कि वे किस लिए हैं, और एक निश्चित अभिन्न साधन क्या हैं। ज्यामितीय अर्थ में, ऐसा अभिन्न क्षेत्रफल के बराबरवक्र f(x), रेखा a और b, और अक्ष ऑक्स से घिरा हुआ चित्र।

चित्र 1 से यह देखा जा सकता है कि निश्चित समाकल वही क्षेत्र है जो छायांकित है भूरे रंग में. आइए इसे एक साधारण उदाहरण से देखें। एकीकरण का उपयोग करके नीचे दी गई छवि में आकृति का क्षेत्रफल ज्ञात करें, और फिर इसकी गणना करें सामान्य तरीके सेलंबाई को चौड़ाई से गुणा करना।

चित्र 2 दर्शाता है कि $ y=f(x)=3 $, $ a=1, b=2 $। अब हम उन्हें समाकलन की परिभाषा में प्रतिस्थापित करते हैं, हम पाते हैं कि $$ S=\int _a ^b f(x) dx = \int _1 ^2 3 dx = $$ $$ =(3x) \Big|_1 ^2 =(3 \ cdot 2)-(3 \cdot 1)=$$ $$=6-3=3 \text(unit)^2 $$ आइए सामान्य तरीके से देखें। हमारे मामले में, लंबाई = 3, आकार की चौड़ाई = 1. $$ S = \text(लंबाई) \cdot \text(चौड़ाई) = 3 \cdot 1 = 3 \text(unit)^2 $$ जैसा कि आप देख सकते हैं, सब कुछ पूरी तरह से मेल खाता था।

प्रश्न उठता है: अनिश्चित समाकलों को कैसे हल किया जाए और उनका अर्थ क्या है? इस तरह के इंटीग्रल का समाधान एंटीडेरिवेटिव फ़ंक्शंस की खोज है। यह प्रक्रिया व्युत्पन्न खोजने के विपरीत है। प्रतिअवकलन ज्ञात करने के लिए, आप गणित में समस्याओं को हल करने में हमारी सहायता का उपयोग कर सकते हैं, या आपको समाकलकों के गुणों और सरलतम प्राथमिक फलनों की समाकलन तालिका को स्वतंत्र रूप से याद रखना चाहिए। ढूँढना इस तरह दिखता है $$ \int f(x) dx = F(x) + C \text(जहां) F(x) $ $ f(x), C = const $ का प्रतिपदार्थ है।

अभिन्न को हल करने के लिए, आपको चर के संबंध में $ f(x) $ फ़ंक्शन को एकीकृत करने की आवश्यकता है। यदि फलन सारणीबद्ध है, तो उत्तर उपयुक्त रूप में लिखा जाता है। यदि नहीं, तो ट्रिकी गणितीय परिवर्तनों द्वारा फ़ंक्शन $ f(x) $ से तालिका फ़ंक्शन प्राप्त करने के लिए प्रक्रिया को कम कर दिया गया है। इसके लिए विभिन्न विधियाँ और गुण हैं, जिनकी चर्चा हम नीचे करेंगे।

तो, आइए अब एक एल्गोरिथम बनाते हैं कि डमी के लिए इंटीग्रल कैसे हल करें?

इंटीग्रल की गणना के लिए एल्गोरिदम

1. निश्चित समाकल ज्ञात कीजिए या नहीं।
2. यदि अपरिभाषित है, तो आपको गणितीय परिवर्तनों का उपयोग करके एकीकृत $ f(x) $ के एंटीडेरिवेटिव फ़ंक्शन $ F(x) $ को खोजने की आवश्यकता है जो फ़ंक्शन $ f(x) $ को एक सारणीबद्ध रूप में लाते हैं।
3. यदि परिभाषित किया गया है, तो चरण 2 को निष्पादित किया जाना चाहिए, और फिर $a$ और $b$ की सीमाओं को एंटीडेरिवेटिव फ़ंक्शन $F(x)$ में प्रतिस्थापित करें। ऐसा करने के लिए किस सूत्र से आप "न्यूटन लाइबनिज फॉर्मूला" लेख में सीखेंगे।

समाधान उदाहरण

तो, आपने सीखा है कि डमी के लिए इंटीग्रल को कैसे हल किया जाए, इंटीग्रल को हल करने के उदाहरणों को अलमारियों पर हल किया गया है। उन्होंने अपना भौतिक और ज्यामितीय अर्थ सीखा। अन्य लेखों में समाधान विधियों पर चर्चा की जाएगी।

आवेदन पत्र

छात्रों और स्कूली बच्चों द्वारा कवर की गई सामग्री को समेकित करने के लिए साइट पर ऑनलाइन इंटीग्रल्स। और अपने व्यावहारिक कौशल का अभ्यास करें। कुछ ही क्षणों में आपके लिए इंटीग्रल ऑनलाइन का संपूर्ण समाधान आपको प्रक्रिया के सभी चरणों को निर्धारित करने में मदद करेगा। हर बार, जैसे ही आप एक इंटीग्रल ऑनलाइन हल करना शुरू करते हैं, आपको इसके प्रकार की पहचान करने की आवश्यकता होती है, इसके बिना आप उपयोग नहीं कर सकते सारणीबद्ध अभिन्न को छोड़कर कोई भी विधि। किसी दिए गए उदाहरण से प्रत्येक तालिका अभिन्न स्पष्ट रूप से दिखाई नहीं दे रही है, कभी-कभी आपको मूल फ़ंक्शन को बदलने की आवश्यकता होती है ताकि एंटीडेरिवेटिव मिल सके। व्यवहार में, समाकलों का समाधान मूल को खोजने की समस्या की व्याख्या करने के लिए नीचे आता है, अर्थात, कार्यों के एक अनंत परिवार से प्रतिपक्षी, लेकिन यदि एकीकरण की सीमाएं दी जाती हैं, तो न्यूटन-लीबनिज़ सूत्र के अनुसार, वहाँ रहता है केवल एक एकल फ़ंक्शन जिसके लिए गणना लागू की जाती है। ऑनलाइन इंटीग्रल ऑनलाइन अनिश्चितकालीन इंटीग्रल और ऑनलाइन निश्चित इंटीग्रल हैं। एक ऑनलाइन फ़ंक्शन का अभिन्न अंग उनके एकीकरण के लिए इच्छित किसी भी संख्या का योग है। इसलिए, अनौपचारिक रूप से, ऑनलाइन निश्चित समाकलन फ़ंक्शन के ग्राफ़ और एकीकरण के भीतर x-अक्ष के बीच का क्षेत्र है। इंटीग्रल के साथ समस्याओं को हल करने के उदाहरण। आइए हम एक चर पर जटिल समाकलन की गणना करें और इसके उत्तर को समस्या के आगे के समाधान से संबंधित करें। जैसा कि वे कहते हैं, आप सीधे इंटीग्रैंड का अभिन्न अंग पा सकते हैं। उच्च सटीकता के साथ कोई भी अभिन्न क्षेत्र निर्धारित करता है रेखाओं से घिरा हुआ आंकड़े। यह इसके ज्यामितीय अर्थों में से एक है। यह विधि छात्रों के लिए चीजों को आसान बनाती है। वास्तव में, कई चरणों का वेक्टर विश्लेषण पर अधिक प्रभाव नहीं पड़ेगा। ऑनलाइन फ़ंक्शन इंटीग्रल इंटीग्रल कैलकुलस की मूल अवधारणा है। अनिश्चितकालीन इंटीग्रल को हल करना। विश्लेषण के मौलिक प्रमेय के अनुसार, समाकलन विभेदन का प्रतिलोम संक्रिया है, जो अवकल समीकरणों को हल करने में मदद करता है। तकनीकी विवरण में भिन्नता, एकीकरण के संचालन की कई अलग-अलग परिभाषाएं हैं। हालांकि, वे सभी संगत हैं, अर्थात्, कोई भी दो एकीकरण विधियां, यदि उन्हें किसी दिए गए फ़ंक्शन पर लागू किया जा सकता है, तो वही परिणाम देगा। रीमैन इंटीग्रल सबसे सरल है - एक निश्चित इंटीग्रल या एक अनिश्चित इंटीग्रल। अनौपचारिक रूप से, एक चर के एक फ़ंक्शन के इंटीग्रल को ग्राफ के तहत क्षेत्र के रूप में पेश किया जा सकता है (फ़ंक्शन के ग्राफ़ और एक्स-अक्ष के बीच संलग्न आंकड़ा)। ऐसी कोई भी उप-समस्या यह साबित करने में सक्षम है कि एक महत्वपूर्ण दृष्टिकोण की शुरुआत में अभिन्न की गणना करना बेहद जरूरी होगा। इसे मत भूलना! इस क्षेत्र को खोजने की कोशिश करते हुए, हम कई ऊर्ध्वाधर आयतों से युक्त आंकड़ों पर विचार कर सकते हैं, जिनमें से आधार एक साथ एकीकरण खंड बनाते हैं और खंड को छोटे खंडों की इसी संख्या में विभाजित करके प्राप्त किया जाता है। ऑनलाइन इंटीग्रल को हल करना ऑनलाइन इंटीग्रल - ऑनलाइन अनिश्चित इंटीग्रल और ऑनलाइन निश्चित इंटीग्रल। ऑनलाइन इंटीग्रल सॉल्विंग: ऑनलाइन अनिश्चितकालीन इंटीग्रल और ऑनलाइन निश्चित इंटीग्रल। कैलकुलेटर कार्यों के विवरण के साथ इंटीग्रल को विस्तार से और मुफ्त में हल करता है! किसी फ़ंक्शन के लिए ऑनलाइन अनिश्चितकालीन अभिन्न, दिए गए फ़ंक्शन के सभी एंटीडेरिवेटिव्स की समग्रता है। यदि कोई फ़ंक्शन एक अंतराल पर परिभाषित और निरंतर है, तो इसका एक एंटीडेरिवेटिव फ़ंक्शन (या एंटीडेरिवेटिव्स का एक परिवार) है। इंटीग्रल केवल एक अभिव्यक्ति को परिभाषित करता है, जिसके लिए ऐसी आवश्यकता होने पर आपके द्वारा निर्धारित की जाती है। इस मामले को ध्यान से देखना और किए गए कार्य से आंतरिक संतुष्टि का अनुभव करना बेहतर है। लेकिन शास्त्रीय एक से अलग तरीके से अभिन्न की गणना करने के लिए, कभी-कभी अप्रत्याशित परिणाम होते हैं और किसी को इस पर आश्चर्य नहीं होना चाहिए। इस तथ्य से प्रसन्न कि जो हो रहा है उस पर सकारात्मक प्रभाव पड़ेगा। पूर्ण विस्तृत चरण-दर-चरण समाधान के साथ निश्चित समाकलों और समाकलों के अनिश्चित समाकलों की सूची। ऑनलाइन एक विस्तृत समाधान के साथ सभी इंटीग्रल। अनिश्चितकालीन अभिन्न। उच्च गणित और विज्ञान की अन्य तकनीकी शाखाओं में अनिश्चितकालीन अभिन्न ऑनलाइन खोजना एक बहुत ही सामान्य कार्य है। एकीकरण के बुनियादी तरीके। इंटीग्रल की परिभाषा, निश्चित और अनिश्चित इंटीग्रल, इंटीग्रल की तालिका, न्यूटन-लीबनिज फॉर्मूला। और फिर, आप अभिन्न अभिव्यक्तियों की तालिका का उपयोग करके अपना अभिन्न पा सकते हैं, लेकिन आपको अभी भी इस पर आने की जरूरत है, क्योंकि सब कुछ उतना सरल नहीं है जितना पहली नज़र में लग सकता है। गलतियाँ मिलने से पहले पूर्ण भवनों के बारे में सोचें। निश्चित समाकलन और इसकी गणना के तरीके। परिवर्तनीय ऊपरी सीमा के साथ ऑनलाइन निश्चित अभिन्न। ऑनलाइन इंटीग्रल्स को हल करना। कोई भी उदाहरण जो सारणीबद्ध सूत्रों का उपयोग करके अभिन्न की गणना करने में मदद करेगा, प्रशिक्षण के किसी भी स्तर के छात्रों के लिए एक उपयोगी मार्गदर्शिका होगी। सही उत्तर की दिशा में सबसे महत्वपूर्ण कदम। इंटीग्रल्स ऑनलाइन। घातीय और लघुगणकीय कार्यों वाले अनिश्चितकालीन समाकलन। इंटीग्रल को ऑनलाइन हल करना - आपको इसके लिए एक विस्तृत समाधान प्राप्त होगा अलग - अलग प्रकारअभिन्न: अनिश्चित, निश्चित, अनुचित। डेफिनिट इंटीग्रल्स कैलकुलेटर संख्यात्मक एकीकरण का उपयोग करके एक अंतराल पर किसी फ़ंक्शन के ऑनलाइन निश्चित इंटीग्रल की गणना करता है। किसी फ़ंक्शन का इंटीग्रल अनुक्रम के योग के समान होता है। अनौपचारिक रूप से, एक निश्चित अभिन्न एक फ़ंक्शन के ग्राफ़ के एक भाग का क्षेत्र है। ऑनलाइन अभिन्न समाधान ऑनलाइन अभिन्न - ऑनलाइन अनिश्चितकालीन अभिन्न और ऑनलाइन निश्चित अभिन्न। अक्सर, ऐसा अभिन्न यह निर्धारित करता है कि एक शरीर की तुलना में समान घनत्व की वस्तु से कितना भारी है, और इससे कोई फर्क नहीं पड़ता कि यह किस आकार का है, क्योंकि सतह पानी को अवशोषित नहीं करती है। ऑनलाइन इंटीग्रल को हल करना .. ऑनलाइन इंटीग्रल - ऑनलाइन अनिश्चित इंटीग्रल और ऑनलाइन निश्चित इंटीग्रल। हर स्नातक छात्र जानता है कि ऑनलाइन इंटीग्रल कैसे खोजा जाए। स्कूली पाठ्यक्रम के आधार पर गणित के इस खंड का भी अध्ययन किया जाता है, लेकिन विस्तार से नहीं, बल्कि इतने जटिल और महत्वपूर्ण विषय की मूल बातें। ज्यादातर मामलों में, छात्र एक व्यापक सिद्धांत के साथ इंटीग्रल का अध्ययन करना शुरू करते हैं, जो कि महत्वपूर्ण विषयों से भी पहले होता है, जैसे कि व्युत्पन्न और सीमा तक मार्ग - वे भी सीमाएं हैं। इंटीग्रल का समाधान धीरे-धीरे सरल कार्यों से सबसे प्राथमिक उदाहरणों से शुरू होता है, और पिछली शताब्दी में और उससे भी पहले प्रस्तावित कई दृष्टिकोणों और नियमों के उपयोग के साथ समाप्त होता है। इंटीग्रल कैलकुलस लिसेयुम और स्कूलों में, यानी माध्यमिक शैक्षणिक संस्थानों में एक खोजपूर्ण प्रकृति का है। हमारी साइट साइट हमेशा आपकी मदद करेगी और ऑनलाइन इंटीग्रल को हल करना आपके लिए एक सामान्य, और सबसे महत्वपूर्ण, समझने योग्य कार्य बन जाएगा। इस संसाधन के आधार पर, आप इस गणितीय खंड में आसानी से उत्कृष्टता प्राप्त कर सकते हैं। नियमों को सीखकर आप चरण दर चरण सीखते हैं, जैसे कि भागों द्वारा एकीकरण या चेबीशेव पद्धति के अनुप्रयोग, आप आसानी से निर्णय ले सकते हैं अधिकतम राशिकिसी भी परीक्षण पर अंक। तो हम अभी भी सभी को ज्ञात इंटीग्रल की तालिका का उपयोग करके इंटीग्रल की गणना कैसे कर सकते हैं, लेकिन इस तरह से कि समाधान सही, सही और सबसे सटीक उत्तर संभव हो? इसे कैसे सीखें और क्या एक साधारण नवसिखुआ के लिए इसे कम से कम समय में करना संभव है? हम इस प्रश्न का उत्तर सकारात्मक में देते हैं - यह संभव है! ऐसे में आप न केवल किसी भी उदाहरण को हल कर पाएंगे, बल्कि एक उच्च श्रेणी के इंजीनियर के स्तर तक भी पहुंच पाएंगे। रहस्य हमेशा की तरह सरल है - आपको अधिक से अधिक प्रयास करने की आवश्यकता है, दे आवश्यक राशिआत्म-प्रशिक्षण का समय। दुर्भाग्य से अभी तक किसी ने दूसरा रास्ता नहीं निकाला है! लेकिन सब कुछ उतना बादल नहीं है जितना पहली नज़र में लगता है। यदि आप इस प्रश्न के साथ हमारी साइट सेवा का संदर्भ लेते हैं, तो हम आपके जीवन को आसान बना देंगे, क्योंकि हमारी साइट ऑनलाइन इंटीग्रल की विस्तार से गणना कर सकती है, और बहुत उच्च गतिऔर बिल्कुल सटीक जवाब। इसके मूल में, इंटीग्रल यह निर्धारित नहीं करता है कि तर्कों का अनुपात पूरे सिस्टम की स्थिरता को कैसे प्रभावित करता है। अगर केवल सब कुछ संतुलित था। आप इस गणितीय विषय की मूल बातें कैसे सीखेंगे, इसके साथ-साथ सेवा किसी भी इंटीग्रैंड का इंटीग्रल ढूंढ सकती है, अगर इस इंटीग्रल को प्राथमिक कार्यों में हल किया जा सकता है। अन्यथा, प्रारंभिक कार्यों में नहीं लिए गए इंटीग्रल के लिए, व्यवहार में एक विश्लेषणात्मक या दूसरे शब्दों में, एक स्पष्ट रूप में उत्तर खोजने की आवश्यकता नहीं है। इंटीग्रल की सभी गणनाएं परिभाषा में कम हो जाती हैं विरोधी व्युत्पन्न कार्यदिए गए इंटीग्रैंड से। ऐसा करने के लिए, पहले ऑनलाइन गणित के सभी नियमों के अनुसार अनिश्चितकालीन अभिन्न की गणना करें। फिर, यदि आवश्यक हो, अभिन्न के ऊपरी और निचले मूल्यों को प्रतिस्थापित करें। यदि आपको निर्धारित करने या गणना करने की आवश्यकता नहीं है अंकीय मूल्य अनिश्चितकालीन अभिन्न, फिर परिणामी एंटीडेरिवेटिव फ़ंक्शन में एक स्थिरांक जोड़ा जाता है, जिससे एंटीडेरिवेटिव फ़ंक्शन के एक परिवार को परिभाषित किया जाता है। विज्ञान में और सामान्य रूप से किसी भी इंजीनियरिंग क्षेत्र में एक विशेष स्थान, जिसमें सातत्य यांत्रिकी शामिल है, एकीकरण संपूर्ण यांत्रिक प्रणालियों, उनके आंदोलनों और बहुत कुछ का वर्णन करता है। कई मामलों में, संकलित अभिन्न एक भौतिक बिंदु की गति के नियम को निर्धारित करता है। यह अनुप्रयुक्त विज्ञान के अध्ययन में एक बहुत ही महत्वपूर्ण उपकरण है। इसके आधार पर, यांत्रिक प्रणालियों के अस्तित्व और व्यवहार के नियमों को निर्धारित करने के लिए बड़े पैमाने पर गणना के बारे में नहीं कहना असंभव है। साइट पर ऑनलाइन इंटीग्रल सॉल्यूशन कैलकुलेटर पेशेवर इंजीनियरों के लिए एक शक्तिशाली उपकरण है। हम आपको स्पष्ट रूप से इसकी गारंटी देते हैं, लेकिन हम आपके इंटीग्रल की गणना तभी कर पाएंगे जब आप इंटीग्रैंड के क्षेत्र में सही एक्सप्रेशन दर्ज करेंगे। गलती करने से डरो मत, इस मामले में सब कुछ ठीक करने योग्य है! आमतौर पर, प्रसिद्ध पाठ्यपुस्तकों या विश्वकोशों से सारणीबद्ध कार्यों के उपयोग के लिए इंटीग्रल का समाधान कम किया जाता है। किसी भी अन्य अनिश्चित समाकल की तरह, इसकी गणना बिना किसी कठोर आलोचना के मानक सूत्र के अनुसार की जाएगी। आसानी से और स्वाभाविक रूप से, प्रथम वर्ष के छात्र मक्खी पर अध्ययन की गई सामग्री को समझ लेते हैं, और कभी-कभी उन्हें अभिन्न खोजने में दो मिनट से अधिक का समय नहीं लगता है। और अगर किसी छात्र ने इंटीग्रल की तालिका सीख ली है, तो सामान्य तौर पर वह अपने दिमाग में उत्तरों को निर्धारित कर सकता है। सतहों के सापेक्ष चर द्वारा कार्यों का विस्तार करने के लिए शुरू में एब्सिस्सा पर किसी बिंदु पर सही वेक्टर दिशा का मतलब है। सतही रेखाओं का अप्रत्याशित व्यवहार गणितीय कार्यों के पारस्परिक स्रोत के आधार के रूप में कुछ अभिन्न अंग लेता है। यदि आप समतल में कट को देखें तो गेंद का बायां किनारा उस बेलन को स्पर्श नहीं करता जिसमें वृत्त अंकित है। सैकड़ों टुकड़े-टुकड़े निरंतर कार्यों में विभाजित छोटे क्षेत्रों का योग दिए गए फ़ंक्शन का ऑनलाइन अभिन्न अंग है। इंटीग्रल का यांत्रिक अर्थ कई लागू समस्याओं में निहित है, यह निकायों की मात्रा का निर्धारण और शरीर द्रव्यमान की गणना है। केवल इन गणनाओं में ट्रिपल और डबल इंटीग्रल शामिल होते हैं। हम जोर देते हैं कि ऑनलाइन इंटीग्रल को केवल अनुभवी शिक्षकों की देखरेख में और कई जाँचों के माध्यम से हल किया जाए। हमसे अक्सर उन छात्रों की प्रगति के बारे में पूछा जाता है जो व्याख्यान में शामिल नहीं होते हैं, उन्हें बिना किसी कारण के छोड़ देते हैं, वे खुद को इंटीग्रल कैसे ढूंढते हैं। हम जवाब देते हैं कि छात्र स्वतंत्र लोग हैं और उन्हें बाहरी रूप से अच्छी तरह से प्रशिक्षित किया जा सकता है, जो आरामदायक घरेलू परिस्थितियों में परीक्षा या परीक्षा की तैयारी कर रहे हैं। कुछ ही सेकंड में, हमारी सेवा किसी भी व्यक्ति की मदद करेगी जो एक चर के संबंध में किसी दिए गए फ़ंक्शन के इंटीग्रल की गणना करना चाहता है। प्रतिअवकलन फलन का अवकलज लेकर प्राप्त परिणाम की जाँच करें। इस मामले में, अभिन्न के समाधान से स्थिरांक गायब हो जाता है। यह नियम स्पष्ट रूप से सभी के लिए है। जैसा कि बहुआयामी संचालन की पुष्टि की जाती है, क्षेत्र को छोटे भागों में विभाजित करने के लिए अनिश्चितकालीन अभिन्न को अक्सर कम कर दिया जाता है। हालांकि, कुछ छात्र और स्कूली बच्चे इस आवश्यकता की उपेक्षा करते हैं। हमेशा की तरह, ऑनलाइन इंटीग्रल को हमारी सेवा साइट द्वारा विस्तार से हल किया जा सकता है और अनुरोधों की संख्या पर कोई प्रतिबंध नहीं है, सब कुछ मुफ़्त है और सभी के लिए उपलब्ध है। ऐसी कई साइटें नहीं हैं जो कुछ ही सेकंड में चरण-दर-चरण उत्तर देती हैं, और सबसे महत्वपूर्ण बात यह है कि उच्च सटीकता के साथ और सुविधाजनक रूप. पांचवें पृष्ठ पर अंतिम उदाहरण में गृहकार्यएक मिले जो चरणों में अभिन्न की गणना करने की आवश्यकता को इंगित करता है। लेकिन हमें यह नहीं भूलना चाहिए कि ऑनलाइन हजारों हल किए गए उदाहरणों पर तैयार की गई सेवा, समय-परीक्षण और परीक्षण का उपयोग करके अभिन्न को कैसे खोजना संभव है। इस तरह का एक अभिन्न प्रणाली की गति को कैसे निर्धारित करता है यह एक चिपचिपा तरल पदार्थ की गति की प्रकृति से स्पष्ट रूप से और स्पष्ट रूप से प्रमाणित होता है, जिसे समीकरणों की इस प्रणाली द्वारा वर्णित किया जाता है।

क्या डिफरेंशियल साइन के तहत नॉन-लीनियर फंक्शन लाना संभव है? हाँ, यदि समाकलन दो कारकों का गुणनफल है: एक कारक कुछ गैर-रैखिक फलनों का एक जटिल फलन है, और दूसरा कारक इस अरैखिक फलन का व्युत्पन्न है। आइए उदाहरणों को देखें।

अनिश्चितकालीन अभिन्न खोजें।

उदाहरण 1. (2x + 1)(x 2 + x + 2) 5 dx = ∫(x 2 + x + 2) 5 d (x 2 + x + 2) =(x²+x+2) 6 : 6+सी.

यह एकीकृत क्या है? काम ऊर्जा समीकरणसे (x 2 + x + 2) और गुणनखंड (2x + 1), जो डिग्री के आधार के व्युत्पन्न के बराबर है: (x 2 + x + 2) "= 2x + 1.

इसने हमें अंतर चिह्न के तहत (2x + 1) लाने की अनुमति दी:

यू 5 डु=यू 6 : 6+ सी। (फॉर्मूला 1)। )

इंतिहान। (एफ (एक्स) + सी)" = ((एक्स² + एक्स + 2) 6 : 6 + सी)′=1/6 6 (एक्स 2 + एक्स + 2) 5 (एक्स 2 + एक्स + 2)" =

\u003d (x 2 + x + 2) 5 (2x + 1) \u003d (2x + 1) (x 2 + x + 2) 5 \u003d f (x)।

उदाहरण 2(3x 2 - 2x + 3)(x 3 - x 2 + 3x + 1) 5 dx = ∫ (x 3 - x 2 + 3x + 1) 5 d (x 3 - x 2 + 3x + 1) =

=(x³- x²+3x+1) 6 : 6+सी

यह उदाहरण उदाहरण 1 से किस प्रकार भिन्न है? कुछ भी तो नहीं! आधार (x 3 - x 2 + 3x + 1) के साथ समान पांचवीं शक्ति को त्रिपद (3x 2 - 2x + 3) से गुणा किया जाता है, जो कि डिग्री के आधार का व्युत्पन्न है: (x 3 - x 2 + 3x + 1) "= 3x 2 - 2x + 3. हम डिग्री के इस आधार को डिफरेंशियल साइन के तहत लाए, जिससे इंटीग्रैंड का मान नहीं बदला, और फिर वही फॉर्मूला 1 लागू किया।) अभिन्न)

उदाहरण 3

यहाँ (2x 3 - 3x) का अवकलज (6x 2 - 3) देगा, और हमारे पास है

वहाँ है (12x 2 - 6), अर्थात्, में व्यंजक 2 गुना अधिक है, तो चलो योग (2x 3 - 3x) अंतर के संकेत के तहत, और कारक को अभिन्न से पहले रखें 2 . आइए सूत्र लागू करें 2) (चादर ).

यहाँ क्या होता है:

आइए जाँच करें, इस पर विचार करते हुए:

उदाहरण। अनिश्चितकालीन अभिन्न खोजें।

1. (6x+5) 3 डीएक्स। हम कैसे तय करेंगे? शीट को देखो और हम कुछ इस तरह तर्क देते हैं: इंटीग्रैंड एक डिग्री है, और हमारे पास डिग्री इंटीग्रल के लिए एक फॉर्मूला है (सूत्र 1) ), लेकिन इसमें डिग्री का आधार तुमऔर एकीकरण चर भी यू

और हमारे पास एक एकीकरण चर है एक्स, और डिग्री का आधार (6x+5). आइए एकीकरण चर में परिवर्तन करें: dx के बजाय हम d (6x+5) लिखते हैं। किया बदल गया? चूंकि, डिफरेंशियल साइन d के बाद जो आता है, वह डिफॉल्ट रूप से डिफरेंशियल होता है,

तब d (6x+5)=6dx, अर्थात्। जब चर x को चर (6x + 5) से बदल दिया जाता है, तो समाकलन 6 गुना बढ़ जाता है, इसलिए हम गुणनखंड 1/6 को पूर्णांक चिह्न के सामने रखते हैं। आप इन तर्कों को इस प्रकार लिख सकते हैं:

इसलिए, हमने इस उदाहरण को एक नया चर पेश करके हल किया (चर x को चर 6x+5 से बदल दिया गया था)। और आपने नया चर (6x + 5) कहाँ लिखा है? अंतर के संकेत के तहत। इसलिए, एक नया चर पेश करने की इस पद्धति को अक्सर कहा जाता है तरीका (या रास्ता ) उपसंहार(नया चर ) अंतर चिह्न के तहत.

दूसरे उदाहरण में, हमने पहले एक ऋणात्मक घातांक के साथ एक डिग्री प्राप्त की, और फिर इसे डिफरेंशियल साइन (7x-2) के तहत अभिव्यक्त किया और डिग्री इंटीग्रल फॉर्मूला का उपयोग किया। 1) (इंटीग्रल्स ).

आइए एक उदाहरण समाधान लेते हैं 3.

समाकलन के पहले गुणांक 1/5 है। क्यों? चूँकि d (5x-2)=5dx, तब, डिफरेंशियल साइन के तहत फंक्शन u=5x-2 को प्रतिस्थापित करते हुए, हमने इंटीग्रैंड को 5 गुना बढ़ा दिया, इसलिए, इस एक्सप्रेशन के मान में बदलाव न हो, इसके लिए यह आवश्यक था। 5 से विभाजित करने के लिए, अर्थात। 1/5 से गुणा करें। इसके बाद, सूत्र का उपयोग किया गया 2) (अभिन्न) .

सभी सरलतम समाकलन सूत्र इस प्रकार दिखाई देंगे:

∫f (एक्स) डीएक्स=एफ (एक्स)+सी, और निम्नलिखित समानता होनी चाहिए:

(एफ (एक्स) + सी) "= एफ (एक्स)।

समेकन सूत्र संगत विभेदन सूत्रों को उलट कर प्राप्त किया जा सकता है।

सचमुच,

प्रतिपादक एनभिन्नात्मक हो सकता है। प्राय: आपको फलन y=√x का अनिश्चित समाकल ज्ञात करना होता है। सूत्र का उपयोग करके फ़ंक्शन f (x)=√x के अभिन्न की गणना करें 1) .

आइए इस उदाहरण को एक सूत्र के रूप में लिखें 2) .

चूंकि (x+C)"=1, तब ∫dx=x+C.

3) dx=x+C.

1 / x² को x -2 से प्रतिस्थापित करते हुए, हम 1 / x² के समाकलन की गणना करते हैं।

और आप यह उत्तर जाने-माने विभेदन सूत्र को उलट कर प्राप्त कर सकते हैं:

हम अपने तर्क को सूत्र के रूप में लिखते हैं 4).

परिणामी समानता के दोनों पक्षों को 2 से गुणा करने पर, हम सूत्र प्राप्त करते हैं 5).

आइए मुख्य त्रिकोणमितीय फलनों के समाकलों का पता लगाएं, उनके अवकलजों को जानते हुए: (sinx)"=cosx; (cosx)"=-sinx; (tgx)"=1/cos²x; (ctgx)"=-1/sin²x। हमें एकीकरण सूत्र मिलते हैं 6) — 9).

6) ∫cosxdx=sinx+C;

7) sinxdx=-cosx+C;

घातांक और लघुगणक फलनों का अध्ययन करने के बाद, हम कुछ और सूत्र जोड़ेंगे।

अनिश्चितकालीन अभिन्न के मूल गुण।

मैं।अनिश्चितकालीन समाकल का अवकलज समाकलन के बराबर होता है .

(∫f(x)dx)"=f(x)।

द्वितीय.अनिश्चितकालीन समाकल का अंतर समाकलन के बराबर होता है।

डी∫एफ (एक्स) डीएक्स = एफ (एक्स) डीएक्स।

III.किसी फलन के अवकलन (व्युत्पन्न) का अनिश्चित समाकल इस फलन के योग और एक मनमाना स्थिरांक C के बराबर होता है।

dF(x)=F(x)+Cया ∫F"(x) dx=F(x)+C.

ध्यान दें: I, II और III गुणों में, अंतर और अभिन्न (अभिन्न और अंतर) के संकेत एक दूसरे को "खाते हैं"!

चतुर्थ।समाकलन के अचर गुणनखंड को समाकल चिह्न से निकाला जा सकता है।

kf (x) dx=k f (x) dx,कहाँ पे कएक स्थिर मान है जो शून्य के बराबर नहीं है।

वीकार्यों के बीजीय योग का समाकलन इन फलनों के समाकलों के बीजगणितीय योग के बराबर होता है।

∫(f (x)±g (x)) dx=∫f (x) dx±∫g (x) dx.

VI.यदि F(x) f(x) और . के लिए एक प्रतिअवकलन है कतथा बीस्थिर मान हैं, और, क≠0, तब (1/k) F (kx+b) f (kx+b) का प्रतिअवकलन है। दरअसल, एक जटिल फ़ंक्शन के व्युत्पन्न की गणना के नियम के अनुसार, हमारे पास है:

तुम लिख सकते हो:

प्रत्येक गणितीय क्रिया के लिए एक व्युत्क्रम क्रिया होती है। विभेदन की क्रिया के लिए (कार्यों के व्युत्पन्न ढूँढना), एक व्युत्क्रम क्रिया भी है - एकीकरण। एकीकरण के माध्यम से, एक फ़ंक्शन उसके दिए गए व्युत्पन्न या अंतर द्वारा पाया (बहाल) पाया जाता है। पाए गए फ़ंक्शन को कहा जाता है प्राचीन.

परिभाषा।विभेदक कार्य एफ (एक्स)फ़ंक्शन के लिए एंटीडेरिवेटिव कहा जाता है एफ (एक्स)किसी दिए गए अंतराल पर, यदि सभी के लिए एक्सइस अंतराल से समानता सत्य है: एफ′ (एक्स) = एफ (एक्स).

उदाहरण। फलन के लिए अवकलज ज्ञात कीजिए: 1) f (x)=2x; 2) f(x)=3cos3x।

1) चूँकि (x²)′=2x, फिर, परिभाषा के अनुसार, फलन F (x)=x² फलन f (x)=2x के लिए प्रतिअवकलन होगा।

2) (sin3x)′=3cos3x। अगर हम f (x)=3cos3x और F (x)=sin3x को निरूपित करते हैं, तो, एंटीडेरिवेटिव की परिभाषा से, हमारे पास है: F′(x)=f (x), और, इसलिए, F (x)=sin3x है f ( x)=3cos3x के लिए एक प्रतिअवकलन।

ध्यान दें कि और (sin3x +5 )′= 3cos3x, और (sin3x -8,2 )′= 3cos3x, ... में सामान्य दृष्टि सेलिखा जा सकता है: (sin3x +सी)′= 3cos3x, कहाँ पे सेकुछ स्थिर मूल्य है। ये उदाहरण भेदभाव की कार्रवाई के विपरीत, एकीकरण की कार्रवाई की अस्पष्टता की बात करते हैं, जब किसी भी अलग-अलग फ़ंक्शन में एक ही व्युत्पन्न होता है।

परिभाषा।यदि समारोह एफ (एक्स)फंक्शन के लिए एंटीडेरिवेटिव है एफ (एक्स)कुछ अंतराल पर, फिर इस फ़ंक्शन के सभी एंटीडेरिवेटिव्स के सेट का रूप है:

एफ (एक्स) + सीजहाँ C कोई वास्तविक संख्या है।

विचाराधीन अंतराल पर फलन f (x) के सभी प्रतिअवकलजों F (x) + C के समुच्चय को अनिश्चित समाकल कहते हैं और इसे प्रतीक द्वारा निरूपित किया जाता है। ∫ (अभिन्न संकेत)। लिखो: ∫f (एक्स) डीएक्स=एफ (एक्स)+सी.

अभिव्यक्ति एफ (एक्स) डीएक्सपढ़ें: "एक्स से डी एक्स तक इंटीग्रल एफई"।

एफ (एक्स) डीएक्सएकीकृत है,

एफ (एक्स)एकीकृत है,

एक्सएकीकरण चर है।

एफ (एक्स)फंक्शन के लिए एंटीडेरिवेटिव है एफ (एक्स),

सेकुछ स्थिर मूल्य है।

अब विचार किए गए उदाहरणों को इस प्रकार लिखा जा सकता है:

1) ∫ 2хdx=x²+C. 2) ∫ 3cos3xdx=sin3x+C.

साइन डी का क्या मतलब है?

डी-डिफरेंशियल साइन - का दोहरा उद्देश्य है: सबसे पहले, यह साइन इंटीग्रेंड को इंटीग्रेशन वेरिएबल से अलग करता है; दूसरे, इस चिन्ह के बाद सब कुछ डिफ़ॉल्ट रूप से विभेदित होता है और एकीकृत द्वारा गुणा किया जाता है।

उदाहरण। इंटीग्रल खोजें: 3) ∫ 2pxdx; 4) ∫ 2pxdp.

3) अंतर चिह्न के बाद डीलागत एक्सएक्स, एक आर

∫ 2хрdx=px²+С. उदाहरण के साथ तुलना करें 1).

चलो एक चेक करते हैं। F′(x)=(px²+C)′=p (x²)′+C′=p 2x=2px=f (x)।

4) अंतर चिह्न के बाद डीलागत आर. तो एकीकरण चर आर, और गुणक एक्सएक स्थिर मूल्य के रूप में माना जाना चाहिए।

∫ 2хрdр=р²х+С. उदाहरणों के साथ तुलना करें 1) तथा 3).

चलो एक चेक करते हैं। F′(p)=(p²x+C)′=x (p²)′+C′=x 2p=2px=f (p)।

1 1 का पेज 1