Das Finden eines unbestimmten Integrals (einer Menge von Stammfunktionen oder „Stammfunktionen“) bedeutet, eine Funktion aus der bekannten Ableitung dieser Funktion zu rekonstruieren. Restaurierter Stammstammsatz F(X) + MIT für Funktion F(X) berücksichtigt die Integrationskonstante C. Basierend auf der Bewegungsgeschwindigkeit eines materiellen Punktes (Ableitung) kann das Bewegungsgesetz dieses Punktes (Stammfunktion) wiederhergestellt werden; entsprechend der Beschleunigung der Bewegung eines Punktes – seiner Geschwindigkeit und dem Bewegungsgesetz. Wie Sie sehen, ist Integration ein weites Feld für die Aktivitäten des Sherlock Holmes der Physik. Und in der Wirtschaftswissenschaft werden viele Konzepte durch Funktionen und deren Ableitungen dargestellt, und daher ist es beispielsweise möglich, die Arbeitsproduktivität in zu verwenden bestimmter Moment Zeit (Ableitung), um das zum entsprechenden Zeitpunkt produzierte Produktionsvolumen wiederherzustellen.

Um ein unbestimmtes Integral zu finden, sind relativ wenige grundlegende Integrationsformeln erforderlich. Aber der Prozess, es zu finden, ist viel schwieriger, als nur diese Formeln anzuwenden. Die ganze Komplexität bezieht sich nicht auf die Integration, sondern darauf, den integrierbaren Ausdruck in eine Form zu bringen, die es ermöglicht, das unbestimmte Integral mithilfe der oben genannten Grundformeln zu finden. Das bedeutet, dass Sie zu Beginn der Integrationspraxis das Gelernte aktivieren müssen weiterführende Schule Fähigkeiten zur Ausdruckstransformation.

Wir werden lernen, Integrale zu finden Eigenschaften und Tabelle der unbestimmten Integrale aus einer Lektion über die Grundkonzepte dieses Themas (öffnet sich in einem neuen Fenster).

Es gibt verschiedene Methoden, um das Integral zu finden Variablenersetzungsmethode Und Integration nach Teilemethode- ein obligatorisches Herrenset für alle, die die höhere Mathematik erfolgreich abgeschlossen haben. Es ist jedoch sinnvoller und angenehmer, mit der Beherrschung der Integration mithilfe der Erweiterungsmethode zu beginnen, basierend auf den folgenden zwei Sätzen zu den Eigenschaften des unbestimmten Integrals, die wir hier der Einfachheit halber wiederholen.

Satz 3. Der konstante Faktor im Integranden kann aus dem Vorzeichen des unbestimmten Integrals entnommen werden, d.h.

Satz 4. Das unbestimmte Integral einer algebraischen Summe einer endlichen Anzahl von Funktionen ist gleich der algebraischen Summe der unbestimmten Integrale dieser Funktionen, d.h.

(2)

Darüber hinaus kann die folgende Regel bei der Integration nützlich sein: Wenn der Ausdruck des Integranden einen konstanten Faktor enthält, wird der Ausdruck der Stammfunktion mit dem Kehrwert des konstanten Faktors multipliziert, d. h

(3)

Da es sich bei dieser Lektion um eine Einführung in die Lösung von Integrationsproblemen handelt, ist es wichtig, zwei Dinge zu beachten, die entweder bereits vorhanden sind Erstphase, oder etwas später überraschen sie Sie vielleicht. Die Überraschung liegt darin begründet, dass die Integration die Umkehroperation der Differentiation ist und das unbestimmte Integral zu Recht als „Stammfunktion“ bezeichnet werden kann.

Das erste, was Sie bei der Integration nicht überraschen sollte. In der Integraltabelle Es gibt Formeln, die keine Analoga zu den Formeln der Ableitungstabelle haben . Dies sind die folgenden Formeln:

Sie können jedoch sicherstellen, dass die Ableitungen der Ausdrücke auf der rechten Seite dieser Formeln mit den entsprechenden Integranden übereinstimmen.

Das zweite, was bei der Integration nicht überraschen sollte. Obwohl die Ableitung jeder Elementarfunktion auch eine Elementarfunktion ist, Unbestimmte Integrale einiger Elementarfunktionen sind keine Elementarfunktionen mehr . Beispiele für solche Integrale könnten die folgenden sein:

Um Integrationstechniken zu entwickeln, sind die folgenden Fähigkeiten nützlich: Brüche reduzieren, ein Polynom im Zähler eines Bruchs durch ein Monom im Nenner dividieren (um die Summe unbestimmter Integrale zu erhalten), Wurzeln in Potenzen umwandeln, ein Monom mit a multiplizieren Polynom, Potenzierung. Diese Fähigkeiten werden für Transformationen des Integranden benötigt, die die Summe der in der Integraltabelle vorhandenen Integrale ergeben sollen.

Gemeinsam unbestimmte Integrale finden

Beispiel 1. Finden Sie das unbestimmte Integral

.

Lösung. Wir sehen im Nenner des Integranden ein Polynom, in dem x quadriert wird. Dies ist ein fast sicheres Zeichen dafür, dass Sie das Tabellenintegral 21 anwenden können (mit einem Arkustangens als Ergebnis). Wir nehmen den Faktor zwei aus dem Nenner heraus (es gibt eine solche Eigenschaft des Integrals – der konstante Faktor kann über das Vorzeichen des Integrals hinaus herausgenommen werden; es wurde oben als Satz 3 erwähnt). Das Ergebnis all dessen:

Nun ist der Nenner die Summe der Quadrate, was bedeutet, dass wir das erwähnte Tabellenintegral anwenden können. Endlich bekommen wir die Antwort:

.

Beispiel 2. Finden Sie das unbestimmte Integral

Lösung. Wir wenden erneut Satz 3 an – die Eigenschaft des Integrals, auf deren Grundlage der konstante Faktor aus dem Vorzeichen des Integrals entnommen werden kann:

Wir wenden Formel 7 aus der Tabelle der Integrale (variabel zu einer Potenz) auf die Integrandenfunktion an:

.

Wir reduzieren die resultierenden Brüche und haben die endgültige Antwort:

Beispiel 3. Finden Sie das unbestimmte Integral

Lösung. Wenn wir zuerst Satz 4 und dann Satz 3 auf Eigenschaften anwenden, finden wir dieses Integral als Summe von drei Integralen:

Alle drei erhaltenen Integrale sind tabellarisch. Wir verwenden Formel (7) aus der Integraltabelle für N = 1/2, N= 2 und N= 1/5, und dann

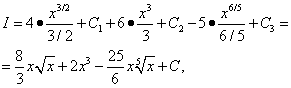
kombiniert alle drei beliebigen Konstanten, die beim Finden der drei Integrale eingeführt wurden. Daher sollte in ähnlichen Situationen nur eine beliebige Integrationskonstante eingeführt werden.

Beispiel 4. Finden Sie das unbestimmte Integral

Lösung. Wenn der Nenner des Integranden ein Monom enthält, können wir den Zähler Term für Term durch den Nenner dividieren. Das ursprüngliche Integral wurde zur Summe zweier Integrale:

.

Um das Tabellenintegral anzuwenden, transformieren wir die Wurzeln in Potenzen und hier ist die endgültige Antwort:

Wir finden weiterhin gemeinsam unbestimmte Integrale

Beispiel 7. Finden Sie das unbestimmte Integral

Lösung. Wenn wir den Integranden transformieren, indem wir das Binomial quadrieren und den Zähler durch den Nenner Term für Term dividieren, dann wird das ursprüngliche Integral zur Summe von drei Integralen.

Es wird ein Überblick über Methoden zur Berechnung unbestimmter Integrale gegeben. Es werden die wichtigsten Integrationsmethoden betrachtet, darunter die Integration von Summe und Differenz, das Platzieren einer Konstante außerhalb des Integralzeichens, das Ersetzen einer Variablen und die partielle Integration. Auch berücksichtigt spezielle Methoden und Techniken zur Integration von Brüchen, Wurzeln, trigonometrischen und exponentiellen Funktionen.

Stammfunktion und unbestimmtes Integral

Eine Stammfunktion F(x) einer Funktion f(x) ist eine Funktion, deren Ableitung gleich f(x) ist:
F′(x) = f(x), x ∈ Δ,
Wo Δ – das Intervall, über das diese Gleichung erfüllt ist.

Die Menge aller Stammfunktionen heißt unbestimmtes Integral:
,
wobei C eine von der Variablen x unabhängige Konstante ist.

Grundformeln und Methoden der Integration

Tabelle der Integrale

Das ultimative Ziel der Berechnung unbestimmter Integrale besteht darin, durch Transformationen ein gegebenes Integral auf einen Ausdruck zu reduzieren, der die einfachsten oder tabellarischen Integrale enthält.
Siehe Tabelle der Integrale >>>

Regel zur Integration von Summen (Differenzen)

Verschieben der Konstante außerhalb des Integralzeichens

Sei c eine von x unabhängige Konstante. Dann lässt sich aus dem Integralzeichen Folgendes entnehmen:

Variablenersatz

Sei x eine Funktion der Variablen t, also x = φ(t).
.
Oder umgekehrt, t = φ(x) ,
.

Mithilfe einer Variablenänderung können Sie nicht nur einfache Integrale berechnen, sondern auch die Berechnung komplexerer Integrale vereinfachen.

Integration nach Teileregel

Integration von Brüchen (rationale Funktionen)

Lassen Sie uns die Notation einführen. Es seien P k (x), Q m (x), R n (x) Polynome der Grade k, m, n in Bezug auf die Variable x.

Betrachten Sie ein Integral, das aus einem Bruch von Polynomen besteht (die sogenannte rationale Funktion):

Wenn k ≥ n, müssen Sie zuerst den ganzen Teil des Bruchs auswählen:
.
Das Integral des Polynoms S k-n (x) wird anhand der Integraltabelle berechnet.

Das Integral bleibt:
, wo m< n .
Um ihn zu berechnen, muss der Integrand in einfache Brüche zerlegt werden.

Dazu müssen Sie die Wurzeln der Gleichung finden:
Q n (x) = 0 .
Anhand der erhaltenen Wurzeln müssen Sie den Nenner als Produkt von Faktoren darstellen:
Q n (x) = s (x-a) n a (x-b) n b ... (x 2 +ex+f) n e (x 2 +gx+k) n g ....
Hier ist s der Koeffizient für x n, x 2 + ex + f > 0, x 2 + gx + k > 0, ....

Zerlegen Sie anschließend den Bruch in seine einfachste Form:

Durch die Integration erhalten wir einen Ausdruck, der aus einfacheren Integralen besteht.
Integrale der Form

werden auf tabellarische Substitution t = x - a reduziert.

Betrachten Sie das Integral:

Lassen Sie uns den Zähler transformieren:
.
Durch Einsetzen in den Integranden erhalten wir einen Ausdruck, der zwei Integrale enthält:
,
.
Die erste wird durch Substitution t = x 2 + ex + f auf eine tabellarische reduziert.
Zweitens gemäß der Reduktionsformel:

wird auf das Integral reduziert

Reduzieren wir seinen Nenner auf die Summe der Quadrate:
.
Dann durch Substitution das Integral

ist ebenfalls tabellarisch aufgeführt.

Integration irrationaler Funktionen

Lassen Sie uns die Notation einführen. Sei R(u 1, u 2, ..., u n) eine rationale Funktion der Variablen u 1, u 2, ..., u n. Also
,
wobei P, Q Polynome in den Variablen u 1, u 2, ..., u n sind.

Bruchlineare Irrationalität

Betrachten wir Integrale der Form:
,
Wo - Rationale Zahlen, m 1 , n 1 , ..., m s , n s - ganze Zahlen.
Sei n der gemeinsame Nenner der Zahlen r 1, ..., r s.
Dann wird das Integral durch Substitution auf das Integral rationaler Funktionen reduziert:
.

Integrale aus Differentialbinomien

Betrachten Sie das Integral:
,
wobei m, n, p rationale Zahlen und a, b reelle Zahlen sind.
Solche Integrale lassen sich in drei Fällen auf Integrale rationaler Funktionen reduzieren.

1) Wenn p eine ganze Zahl ist. Substitution x = t N, wobei N der gemeinsame Nenner der Brüche m und n ist.
2) Wenn – eine ganze Zahl. Substitution a x n + b = t M, wobei M der Nenner der Zahl p ist.
3) Wenn – eine ganze Zahl. Substitution a + b x - n = t M, wobei M der Nenner der Zahl p ist.

Wenn keine der drei Zahlen eine ganze Zahl ist, können Integrale dieser Art nach dem Satz von Tschebyschew nicht durch eine endliche Kombination von Elementarfunktionen ausgedrückt werden.

In manchen Fällen ist es zunächst sinnvoll, das Integral auf günstigere Werte m und p zu reduzieren. Dies kann mithilfe von Reduktionsformeln erfolgen:
;
.

Integrale, die die Quadratwurzel eines Quadrattrinoms enthalten

Hier betrachten wir Integrale der Form:
,

Euler-Ersetzungen

Solche Integrale können auf Integrale rationaler Funktionen einer von drei Euler-Substitutionen reduziert werden:
, für a > 0;
, für c > 0 ;
, wobei x 1 die Wurzel der Gleichung a x 2 + b x + c = 0 ist. Wenn diese Gleichung echte Wurzeln hat.

Trigonometrische und hyperbolische Substitutionen

Direkte Methoden

In den meisten Fällen führen Euler-Substitutionen zu längeren Berechnungen als direkte Methoden. Mit direkten Methoden wird das Integral auf eine der unten aufgeführten Formen reduziert.

Tippe I

Integral der Form:
,
wobei P n (x) ein Polynom vom Grad n ist.

Solche Integrale werden mit der Methode der unbestimmten Koeffizienten unter Verwendung der Identität gefunden:

Wenn wir diese Gleichung differenzieren und die linke und rechte Seite gleichsetzen, finden wir die Koeffizienten A i.

Typ II

Integral der Form:
,
wobei P m (x) ein Polynom vom Grad m ist.

Substitution t = (x - α) -1 Dieses Integral wird auf den vorherigen Typ reduziert. Wenn m ≥ n, dann sollte der Bruch einen ganzzahligen Teil haben.

Typ III

Der dritte und komplexeste Typ:
.

Hier müssen Sie eine Substitution vornehmen:
.
Danach nimmt das Integral die Form an:
.
Als nächstes müssen die Konstanten α, β so gewählt werden, dass die Koeffizienten für t Null werden:
B = 0, B 1 = 0.
Dann zerfällt das Integral in die Summe von Integralen zweier Typen:
;
,
die jeweils durch Substitutionen integriert werden:
z 2 = A 1 t 2 + C 1 ;
y 2 = A 1 + C 1 t -2 .

Allgemeiner Fall

Integration transzendentaler (trigonometrischer und exponentieller) Funktionen

Beachten wir vorab, dass die Methoden, die für trigonometrische Funktionen anwendbar sind, auch für hyperbolische Funktionen anwendbar sind. Aus diesem Grund werden wir die Integration hyperbolischer Funktionen nicht gesondert betrachten.

Integration rationaler trigonometrischer Funktionen von cos x und sin x

Betrachten wir Integrale trigonometrischer Funktionen der Form:
,
wobei R eine rationale Funktion ist. Dazu können auch Tangens und Kotangens gehören, die mithilfe von Sinus und Cosinus umgerechnet werden sollten.

Bei der Integration solcher Funktionen ist es sinnvoll, drei Regeln zu beachten:
1) wenn R( cos x, sin x) multipliziert mit -1 ab dem Vorzeichenwechsel vor einer der Größen weil x oder Sünde x, dann ist es sinnvoll, den anderen von ihnen mit t zu bezeichnen.
2) wenn R( cos x, sin x)ändert sich durch einen gleichzeitigen Vorzeichenwechsel nicht weil x Und Sünde x, dann ist es sinnvoll zu setzen tg x = t oder Kinderbett x = t.
3) Substitution führt in allen Fällen zum Integral eines rationalen Bruchs. Leider führt diese Ersetzung ggf. zu längeren Berechnungen als die vorherigen.

Produkt der Potenzfunktionen von cos x und sin x

Betrachten wir Integrale der Form:

Wenn m und n rationale Zahlen sind, dann ist eine der Substitutionen t = Sünde x oder t = weil x das Integral wird auf das Integral des Differentialbinomials reduziert.

Wenn m und n ganze Zahlen sind, werden die Integrale durch partielle Integration berechnet. Daraus ergeben sich folgende Reduktionsformeln:

;
;
;
.

Integration in Teilstücken

Anwendung der Eulerschen Formel

Wenn der Integrand bezüglich einer der Funktionen linear ist
Cos Axt oder sinax, dann ist es praktisch, die Eulersche Formel anzuwenden:
e iax = cos ax + isin ax(wobei i 2 = - 1 ),
Ersetzen dieser Funktion durch e iax und Hervorheben des echten (beim Ersetzen). Cos Axt) oder Imaginärteil (beim Ersetzen sinax) aus dem erhaltenen Ergebnis.

Verweise:
N.M. Gunter, R.O. Kuzmin, Sammlung von Problemen der höheren Mathematik, „Lan“, 2003.

Der Prozess der Lösung von Integralen in der Wissenschaft namens Mathematik wird Integration genannt. Mithilfe der Integration können Sie einige physikalische Größen ermitteln: Fläche, Volumen, Körpermasse und vieles mehr.

Integrale können unbestimmt oder bestimmt sein. Betrachten wir die Form des bestimmten Integrals und versuchen wir, seine physikalische Bedeutung zu verstehen. Es wird in dieser Form dargestellt: $$ \int ^a _b f(x) dx $$. Besonderheit Das Schreiben eines bestimmten Integrals eines unbestimmten Integrals bedeutet, dass es Grenzen der Integration von a und b gibt. Jetzt erfahren wir, warum sie benötigt werden und was ein bestimmtes Integral eigentlich bedeutet. Im geometrischen Sinne ist ein solches Integral gleich der Fläche der Figur, die durch die Kurve f(x), die Linien a und b und die Ox-Achse begrenzt wird.

Aus Abb. 1 geht hervor, dass das bestimmte Integral die gleiche Fläche ist, die schattiert ist grau. Lassen Sie uns dies anhand eines einfachen Beispiels überprüfen. Lassen Sie uns mithilfe der Integration die Fläche der Abbildung im Bild unten ermitteln und sie dann berechnen in gewohnter Weise Länge mit Breite multiplizieren.

Aus Abb. 2 ist klar, dass $ y=f(x)=3 $, $ a=1, b=2 $. Wenn wir sie nun in die Definition des Integrals einsetzen, erhalten wir $$ S=\int _a ^b f(x) dx = \int _1 ^2 3 dx = $$ $$ =(3x) \Big|_1 ^2 =(3 \ cdot 2)-(3 \cdot 1)=$$ $$=6-3=3 \text(units)^2 $$ Lassen Sie uns die Prüfung auf die übliche Weise durchführen. In unserem Fall ist die Länge = 3, die Breite der Figur = 1. $$ S = \text(length) \cdot \text(width) = 3 \cdot 1 = 3 \text(units)^2 $$ Wie Sie können Sehen Sie, alles passt perfekt.

Es stellt sich die Frage: Wie löst man unbestimmte Integrale und was bedeuten sie? Das Lösen solcher Integrale bedeutet, Stammfunktionen zu finden. Dieser Vorgang ist das Gegenteil der Ermittlung der Ableitung. Um die Stammfunktion zu finden, können Sie unsere Hilfe bei der Lösung mathematischer Probleme in Anspruch nehmen oder Sie müssen sich selbstständig die Eigenschaften von Integralen und die Integrationstabelle der einfachsten Elementarfunktionen merken. Das Ergebnis sieht so aus: $$ \int f(x) dx = F(x) + C \text(wobei) F(x) $ die Stammfunktion von $ f(x) ist, C = const $.

Um das Integral zu lösen, müssen Sie die Funktion $ f(x) $ über eine Variable integrieren. Wenn die Funktion tabellarisch ist, wird die Antwort in der entsprechenden Form geschrieben. Wenn nicht, läuft der Prozess darauf hinaus, aus der Funktion $ f(x) $ durch knifflige mathematische Transformationen eine Tabellenfunktion zu erhalten. Hierfür gibt es verschiedene Methoden und Eigenschaften, die wir weiter betrachten werden.

Erstellen wir nun einen Algorithmus zum Lösen von Integralen für Dummies?

Algorithmus zur Berechnung von Integralen

1. Lassen Sie uns herausfinden, ob das bestimmte Integral vorliegt oder nicht.
2. Wenn nicht definiert, müssen Sie die Stammfunktion $ F(x) $ des Integranden $ f(x) $ mithilfe mathematischer Transformationen finden, die zu einer tabellarischen Form der Funktion $ f(x) $ führen.
3. Wenn definiert, müssen Sie Schritt 2 ausführen und dann die Grenzwerte $ a $ und $ b $ in die Stammfunktion $ F(x) $ einsetzen. Mit welcher Formel Sie das erreichen, erfahren Sie im Artikel „Newton-Leibniz-Formel“.

Beispiele für Lösungen

Sie haben also gelernt, wie man Integrale für Dummies löst, Beispiele für die Lösung von Integralen wurden aussortiert. Wir lernten ihre physikalische und geometrische Bedeutung kennen. Die Lösungsmethoden werden in anderen Artikeln beschrieben.

Anwendung

Online-Integrale auf der Website für Studenten und Schüler zur Festigung des behandelten Materials. Und trainieren Sie Ihre praktischen Fähigkeiten. Eine vollständige Online-Lösung von Integralen für Sie in wenigen Augenblicken wird Ihnen helfen, alle Phasen des Prozesses zu bestimmen. Jedes Mal, wenn Sie mit der Online-Lösung eines Integrals beginnen, müssen Sie seinen Typ identifizieren; ohne dies können Sie keine einzelne Methode verwenden, es sei denn Sie betrachten das Integral als tabellarisch. Nicht jedes Tabellenintegral ist aus einem gegebenen Beispiel klar ersichtlich; manchmal muss man die ursprüngliche Funktion transformieren, um die Stammfunktion zu finden. In der Praxis kommt es bei der Lösung von Integralen darauf an, das Problem zu interpretieren, das Original, also die Stammfunktion aus einer unendlichen Familie von Funktionen zu finden, aber wenn die Grenzen der Integration gegeben sind, dann gibt es nach der Newton-Leibniz-Formel nur eine einzige Funktion übrig, um Berechnungen anzuwenden. Online-Integrale – Online-unbestimmtes Integral und Online-bestimmtes Integral. Das Integral einer Funktion online ist die Summe aller Zahlen, die zu ihrer Integration vorgesehen sind. Daher ist das Online-Definitivintegral informell die Fläche zwischen dem Graphen der Funktion und der x-Achse innerhalb der Integrationsgrenzen. Beispiele für die Lösung von Problemen mit Integralen. Lassen Sie uns ein komplexes Integral über eine Variable auswerten und seine Antwort mit der weiteren Lösung des Problems in Beziehung setzen. Es ist, wie man sagt, möglich, das Integral des Integranden direkt zu finden. Jedes Integral bestimmt die Fläche mit hoher Genauigkeit durch Linien begrenzt Figuren. Dies ist eine seiner geometrischen Bedeutungen. Diese Methode erleichtert den Studierenden die Arbeit. Tatsächlich haben mehrere Schritte keinen großen Einfluss auf die Vektoranalyse. Das Integral einer Funktion online ist das Grundkonzept der Integralrechnung. Lösen unbestimmter Integrale. Nach dem Hauptsatz der Analysis ist Integration die Umkehroperation der Differentiation, die zur Lösung von Differentialgleichungen beiträgt. Es gibt verschiedene Definitionen des Integrationsvorgangs, die sich in technischen Details unterscheiden. Sie sind jedoch alle kompatibel, d. h. zwei beliebige Integrationsmethoden liefern das gleiche Ergebnis, wenn sie auf eine bestimmte Funktion angewendet werden können. Das einfachste ist das Riemannsche Integral – ein bestimmtes Integral oder ein unbestimmtes Integral. Informell kann das Integral einer Funktion einer Variablen als Fläche unter dem Graphen eingeführt werden (die Zahl, die zwischen dem Graphen der Funktion und der x-Achse eingeschlossen ist). Jedes dieser Teilprobleme kann rechtfertigen, dass die Berechnung des Integrals zu Beginn eines wichtigen Ansatzes äußerst notwendig sein wird. Vergiss das nicht! Um diesen Bereich zu finden, können wir uns Figuren vorstellen, die aus einer bestimmten Anzahl vertikaler Rechtecke bestehen, deren Basen zusammen ein Integrationssegment bilden und durch Unterteilung des Segments in die entsprechende Anzahl kleiner Segmente erhalten werden. Integrale online lösen. Integral online – unbestimmtes Integral online und bestimmtes Integral online. Integrale online lösen: Online unbestimmtes Integral und online bestimmtes Integral. Der Rechner löst Integrale mit detaillierter Beschreibung der Aktionen und das kostenlos! Ein unbestimmtes Online-Integral für eine Funktion ist die Menge aller Stammfunktionen einer gegebenen Funktion. Wenn eine Funktion definiert und in einem Intervall stetig ist, dann gibt es für sie eine Stammfunktion (oder eine Familie von Stammfunktionen). Das Integral definiert lediglich einen Ausdruck, dessen Bedingungen Sie bei Eintreten eines solchen Bedarfs festlegen. Es ist besser, diese Angelegenheit behutsam anzugehen und durch die geleistete Arbeit innere Zufriedenheit zu erfahren. Aber die Berechnung des Integrals mit einer anderen als der klassischen Methode führt manchmal zu unerwarteten Ergebnissen, und darüber sollte man sich nicht wundern. Ich freue mich, dass diese Tatsache eine positive Resonanz auf das Geschehen haben wird. Liste der bestimmten Integrale und unbestimmten Integrale von Integralen mit vollständiger, detaillierter Schritt-für-Schritt-Lösung. Alle Integrale mit detaillierten Lösungen online. Unbestimmtes Integral. Das unbestimmte Integral online zu finden, ist ein sehr häufiges Problem in der höheren Mathematik und anderen technischen Bereichen der Naturwissenschaften. Grundlegende Methoden der Integration. Definition von Integral, bestimmtem und unbestimmtem Integral, Integraltabelle, Newton-Leibniz-Formel. Auch hier können Sie Ihr Integral mithilfe der Tabelle der Integralausdrücke finden, dies muss jedoch noch erreicht werden, da nicht alles so einfach ist, wie es auf den ersten Blick erscheinen mag. Denken Sie über fertiggestellte Gebäude nach, bevor Fehler gefunden werden. Bestimmtes Integral und Methoden zu seiner Berechnung. Online bestimmtes Integral mit variabler Obergrenze. Integrale online lösen. Jedes Beispiel, das bei der Berechnung des Integrals mithilfe tabellarischer Formeln hilft, ist ein nützlicher Leitfaden für Schüler aller Ausbildungsstufen. Der wichtigste Schritt zur richtigen Antwort. Integrale online. Nicht bestimmte Integrale, enthält Exponential- und Logarithmusfunktionen. Integrale online lösen - Sie erhalten eine detaillierte Lösung für verschiedene Typen Integrale: unbestimmt, bestimmt, uneigentlich. Der Rechner für bestimmte Integrale berechnet online das bestimmte Integral einer Funktion über ein Intervall mithilfe numerischer Integration. Das Integral einer Funktion ist ein Analogon der Summe einer Folge. Informell ausgedrückt ist ein bestimmtes Integral die Fläche eines Teils des Graphen einer Funktion. Das Integral online lösen. Integral online – unbestimmtes Integral online und bestimmtes Integral online. Oftmals bestimmt ein solches Integral, wie viel schwerer ein Körper im Vergleich zu einem Körper gleicher Dichte ist, und dabei spielt es keine Rolle, welche Form er hat, da die Oberfläche kein Wasser aufnimmt. Integrale online lösen. Integrale online – unbestimmte Integrale online und bestimmte Integrale online. Jeder junge Student weiß, wie man das Integral online findet. Auf der Grundlage des schulischen Lehrplans wird auch dieser Teil der Mathematik studiert, allerdings nicht im Detail, sondern nur die Grundlagen eines so komplexen und wichtigen Themas. In den meisten Fällen beginnt das Studium der Integrale mit einer ausführlichen Theorie, der auch wichtige Themen vorangestellt sind, wie zum Beispiel Ableitungen und Übergang zu Grenzwerten – sie sind auch Grenzwerte. Die Lösung von Integralen beginnt schrittweise mit den elementarsten Beispielen einfacher Funktionen und endet mit der Verwendung vieler Ansätze und Regeln, die im letzten Jahrhundert und sogar noch viel früher vorgeschlagen wurden. Die Integralrechnung dient Bildungszwecken in Lyzeen und Schulen, also in weiterführenden Bildungseinrichtungen. Unsere Website hilft Ihnen immer weiter und die Online-Lösung von Integralen wird für Sie zur Selbstverständlichkeit und vor allem zu einer verständlichen Aufgabe. Basierend auf dieser Ressource können Sie in diesem mathematischen Abschnitt leicht Perfektion erreichen. Wenn Sie die Regeln verstehen, die Sie Schritt für Schritt erlernen, wie etwa die partielle Integration oder die Anwendung der Tschebyscheff-Methode, können Sie sich leicht entscheiden Höchstbetrag Punkte für jeden Test. Wie können wir also das Integral noch anhand der bekannten Integraltabelle berechnen, aber so, dass die Lösung richtig, korrekt und mit einer möglichst genauen Antwort ist? Wie lernt man das und kann ein gewöhnlicher Studienanfänger es in kürzester Zeit schaffen? Beantworten wir diese Frage mit Ja – das können Sie! Gleichzeitig können Sie nicht nur jedes Beispiel lösen, sondern auch das Niveau eines hochqualifizierten Ingenieurs erreichen. Das Geheimnis ist einfacher denn je – Sie müssen sich maximal anstrengen und sich widmen erforderliche Menge Zeit zur Selbstvorbereitung. Leider ist bisher noch niemand auf eine andere Möglichkeit gekommen! Doch nicht alles ist so bewölkt, wie es auf den ersten Blick scheint. Wenn Sie sich mit dieser Frage an unsere Service-Website wenden, machen wir Ihnen das Leben leichter, denn auf unserer Website können Sie Integrale detailliert und mit sehr viel Aufwand online berechnen hohe Geschwindigkeit und eine tadellos genaue Antwort. Im Kern bestimmt das Integral nicht, wie sich das Verhältnis der Argumente auf die Stabilität des Gesamtsystems auswirkt. Wenn nur alles ausgeglichen wäre. Während Sie die Grundlagen dieses mathematischen Themas erlernen, kann der Dienst das Integral eines beliebigen Integranden finden, wenn dieses Integral in Elementarfunktionen aufgelöst werden kann. Ansonsten ist es für Integrale, die nicht in Elementarfunktionen genommen werden, in der Praxis nicht notwendig, die Antwort in analytischer oder mit anderen Worten in expliziter Form zu finden. Alle Integralberechnungen werden auf die Definition reduziert Stammfunktion aus der gegebenen Integrandenfunktion. Berechnen Sie dazu zunächst online das unbestimmte Integral nach allen Gesetzen der Mathematik. Ersetzen Sie dann gegebenenfalls die oberen und unteren Werte des Integrals. Wenn Sie nicht bestimmen oder berechnen müssen Zahlenwert unbestimmtes Integral, dann wird der resultierenden Stammfunktion eine Konstante hinzugefügt, wodurch eine Familie von Stammfunktionen definiert wird. Integration nimmt in der Wissenschaft und in jedem Ingenieurbereich im Allgemeinen, einschließlich der Kontinuumsmechanik, einen besonderen Platz ein; sie beschreibt ganze mechanische Systeme, ihre Bewegungen und vieles mehr. In vielen Fällen bestimmt das gebildete Integral das Bewegungsgesetz eines materiellen Punktes. Es ist ein sehr wichtiges Werkzeug im Studium der angewandten Wissenschaften. Auf dieser Grundlage kann man nicht umhin, groß angelegte Berechnungen zur Bestimmung der Existenz- und Verhaltensgesetze mechanischer Systeme zu erwähnen. Der Online-Rechner zur Lösung von Integralen auf der Website ist ein leistungsstarkes Werkzeug für professionelle Ingenieure. Das garantieren wir Ihnen auf jeden Fall, aber wir können Ihr Integral erst berechnen, wenn Sie den richtigen Ausdruck in den Bereich des Integranden eingeben. Haben Sie keine Angst, Fehler zu machen, in dieser Angelegenheit kann alles korrigiert werden! Normalerweise kommt es bei der Lösung von Integralen darauf an, tabellarische Funktionen aus bekannten Lehrbüchern oder Enzyklopädien zu verwenden. Wie jedes andere unbestimmte Integral wird es ohne größere Kritikpunkte mit der Standardformel berechnet. Studienanfänger erfassen den Stoff, den sie gelernt haben, auf der Stelle leicht und natürlich, und für die Integralfindung dauert es manchmal nicht länger als zwei Minuten. Und wenn ein Schüler die Integraltabelle gelernt hat, kann er die Antworten in der Regel im Kopf ermitteln. Die Erweiterung von Funktionen um Variablen relativ zu Flächen bedeutet zunächst die korrekte Vektorrichtung an einem Abszissenpunkt. Das unvorhersehbare Verhalten von Oberflächenlinien basiert auf bestimmten Integralen als Antwortquelle mathematischer Funktionen. Der linke Rand der Kugel berührt nicht den Zylinder, in den der Kreis eingeschrieben ist, wenn man den Schnitt in einer Ebene betrachtet. Die Summe kleiner Flächen, die in Hunderte stückweise stetiger Funktionen unterteilt sind, ist das Online-Integral einer gegebenen Funktion. Die mechanische Bedeutung des Integrals liegt in vielen angewandten Problemen, beispielsweise der Bestimmung des Volumens von Körpern und der Berechnung der Masse eines Körpers. Bei diesen Berechnungen kommen Tripel- und Doppelintegrale zum Einsatz. Wir bestehen darauf, dass die Online-Lösung von Integralen nur unter der Aufsicht erfahrener Lehrkräfte und durch zahlreiche Kontrollen erfolgt. Wir werden oft nach der Leistung von Studierenden gefragt, die keine Vorlesungen besuchen, diese grundlos schwänzen und wie sie es schaffen, sie zu finden das Integral selbst. Wir antworten, dass Studenten freie Menschen sind und durchaus in der Lage sind, extern zu lernen und sich bequem von zu Hause aus auf einen Test oder eine Prüfung vorzubereiten. Unser Service hilft jedem in Sekundenschnelle, das Integral einer bestimmten Funktion über eine Variable zu berechnen. Das erhaltene Ergebnis sollte durch Bildung der Ableitung der Stammfunktion überprüft werden. In diesem Fall wird die Konstante aus der Lösung des Integrals Null. Diese Regel gilt natürlich für alle. Da multidirektionale Operationen gerechtfertigt sind, wird das unbestimmte Integral oft auf die Aufteilung des Definitionsbereichs in kleine Teile reduziert. Allerdings vernachlässigen einige Studierende und Schüler diese Vorgabe. Wie immer können Online-Integrale detailliert über unsere Service-Website gelöst werden und es gibt keine Einschränkungen hinsichtlich der Anzahl der Anfragen, alles ist kostenlos und für jedermann verfügbar. Es gibt nicht viele Websites, die eine Schritt-für-Schritt-Antwort in Sekundenschnelle und vor allem mit hoher Genauigkeit und Genauigkeit bereitstellen praktische Form. Im letzten Beispiel auf Seite fünf Hausaufgaben Ich bin auf eine gestoßen, die darauf hinweist, dass das Integral Schritt für Schritt berechnet werden muss. Aber wir dürfen nicht vergessen, wie es möglich ist, das Integral mithilfe eines vorgefertigten Dienstes zu finden, der online an Tausenden von gelösten Beispielen getestet und getestet wurde. Wie ein solches Integral die Bewegung des Systems bestimmt, wird uns durch die Art der Bewegung der viskosen Flüssigkeit, die durch dieses Gleichungssystem beschrieben wird, klar und deutlich vor Augen geführt.

Ist es möglich, eine nichtlineare Funktion unter dem Differentialzeichen zu subsumieren? Ja, wenn der Integrand das Produkt zweier Faktoren ist: Ein Faktor ist eine komplexe Funktion einer nichtlinearen Funktion und der andere Faktor ist die Ableitung dieser nichtlinearen Funktion. Schauen wir uns das Gesagte anhand von Beispielen an.

Finden Sie unbestimmte Integrale.

Beispiel 1. ∫(2x + 1)(x 2 + x + 2) 5 dx = ∫(x 2 + x + 2) 5 d (x 2 + x + 2) =(x²+x+2) 6 : 6 + C.

Was stellt dieser Integrand dar? Arbeiten Power-Funktion aus (x 2 + x + 2) und dem Multiplikator (2x + 1), der gleich der Ableitung der Basis der Potenz ist: (x 2 + x + 2)“ = 2x + 1.

Dadurch konnten wir (2x + 1) unter das Differentialzeichen setzen:

∫u 5 du=u 6 : 6+ C. (Formel 1). )

Untersuchung. (F (x)+ C)" =((x²+x+2) 6 : 6 + C)′=1/6 6 (x 2 + x + 2) 5 (x 2 + x + 2)" =

=(x 2 + x + 2) 5 · (2x + 1) = (2x + 1)(x 2 + x + 2) 5 = f (x).

Beispiel 2.∫(3x 2 – 2x + 3)(x 3 – x 2 + 3x + 1) 5 dx = ∫(x 3 – x 2 + 3x + 1) 5 d (x 3 – x 2 + 3x + 1) =

=(x³- x²+3x+1) 6 : 6+C

Und wie unterscheidet sich dieses Beispiel von Beispiel 1? Nichts! Dieselbe fünfte Potenz mit der Basis (x 3 – x 2 + 3x + 1) wird mit dem Trinom (3x 2 – 2x + 3) multipliziert, das die Ableitung der Basis der Potenz ist: (x 3 – x 2 + 3x + 1)" = 3x 2 – 2x + 3. Wir haben diese Basis des Grades unter das Differentialzeichen gebracht, von dem aus sich der Wert des Integranden nicht geändert hat, und dann die gleiche Formel 1) angewendet. Integrale)

Beispiel 3.

Hier ergibt die Ableitung von (2x 3 – 3x) (6x 2 – 3), und bei uns

es gibt (12x 2 – 6), also den Ausdruck in 2 mal größer, das heißt, wir setzen (2x 3 – 3x) unter das Differentialzeichen und einen Faktor vor das Integral 2 . Wenden wir die Formel an 2) ( Blatt ).

Folgendes passiert:

Lassen Sie uns dies überprüfen und dabei Folgendes berücksichtigen:

Beispiele. Finden Sie unbestimmte Integrale.

1. ∫(6x+5) 3 dx. Wie werden wir entscheiden? Blick auf das Blatt und wir argumentieren etwa so: Der Integrand stellt einen Grad dar, und wir haben eine Formel für das Integral des Grades (Formel 1) ), sondern darin die Grundlage des Abschlusses u und auch die Integrationsvariable u.

Und wir haben eine Integrationsvariable X und die Basis des Abschlusses (6x+5). Nehmen wir eine Änderung an der Integrationsvariablen vor: Anstelle von dx schreiben wir d (6x+5). Was hat sich geändert? Da das, was nach dem Differentialzeichen d kommt, standardmäßig differenziert ist,

dann d (6x+5)=6dx, d.h. Beim Ersetzen der Variablen x durch die Variable (6x+5) erhöhte sich die Integrandenfunktion um das Sechsfache, daher setzen wir den Faktor 1/6 vor das Integralzeichen. Diese Argumente können wie folgt geschrieben werden:

Also haben wir dieses Beispiel gelöst, indem wir eine neue Variable eingeführt haben (die Variable x wurde durch die Variable 6x+5 ersetzt). Wo haben Sie die neue Variable (6x+5) geschrieben? Unter dem Differentialzeichen. Daher wird diese Methode zum Einführen einer neuen Variablen häufig aufgerufen Methode ( oder Weg ) zusammenfassen(neue Variable ) unter dem Differentialzeichen.

Im zweiten Beispiel haben wir zunächst einen Grad mit negativem Exponenten erhalten, diesen dann unter dem Differentialzeichen (7x-2) subsumiert und die Formel für das Integral des Grades verwendet 1) (Integrale ).

Schauen wir uns die Beispiellösung an 3.

Dem Integral ist ein Koeffizient von 1/5 vorangestellt. Warum? Da d (5x-2) = 5dx ist, haben wir durch Einsetzen der Funktion u = 5x-2 unter das Differentialzeichen den Integranden um das Fünffache erhöht, damit sich der Wert dieses Ausdrucks nicht ändert notwendig, durch 5 zu dividieren, d.h. . mit 1/5 multiplizieren. Als nächstes wurde die Formel verwendet 2) (Integrale) .

Alle einfachsten Integralformeln sehen so aus:

∫f (x) dx=F (x)+C, und die Gleichheit muss erfüllt sein:

(F (x)+C)"=f (x).

Integrationsformeln können durch Invertieren der entsprechenden Differenzierungsformeln erhalten werden.

Wirklich,

Exponent N kann gebrochen sein. Oft muss man das unbestimmte Integral der Funktion y=√x finden. Berechnen wir das Integral der Funktion f (x)=√x anhand der Formel 1) .

Schreiben wir dieses Beispiel als Formel 2) .

Da (x+C)"=1, dann ist ∫dx=x+C.

3) ∫dx=x+C.

Indem wir 1/x² durch x -2 ersetzen, berechnen wir das Integral von 1/x².

Und diese Antwort konnte man durch Umkehrung der bekannten Differenzierungsformel erhalten:

Schreiben wir unsere Argumentation in Form einer Formel 4).

Wenn wir beide Seiten der resultierenden Gleichheit mit 2 multiplizieren, erhalten wir die Formel 5).

Finden wir die Integrale der wichtigsten trigonometrischen Funktionen und kennen ihre Ableitungen: (sinx)"=cosx; (cosx)"=-sinx; (tgx)"=1/cos²x; (ctgx)"=-1/sin²x. Wir erhalten die Integrationsformeln 6) — 9).

6) ∫cosxdx=sinx+C;

7) ∫sinxdx=-cosx+C;

Nachdem wir die Exponential- und Logarithmusfunktionen studiert haben, fügen wir noch ein paar weitere Formeln hinzu.

Grundlegende Eigenschaften des unbestimmten Integrals.

ICH. Die Ableitung des unbestimmten Integrals ist gleich dem Integranden .

(∫f (x) dx)"=f (x).

II. Das Differential des unbestimmten Integrals ist gleich dem Integranden.

d∫f (x) dx=f (x) dx.

III. Das unbestimmte Integral des Differentials (Ableitung) einer Funktion ist gleich der Summe dieser Funktion und einer beliebigen Konstante C.

∫dF (x)=F (x)+C oder ∫F"(x) dx=F (x)+C.

Bitte beachten Sie: In den Eigenschaften I, II und III „fressen“ sich die Vorzeichen von Differential und Integral (Integral und Differential) gegenseitig!

IV. Aus dem Integralzeichen kann der konstante Faktor des Integranden entnommen werden.

∫kf (x) dx=k ∫f (x) dx, Wo k- ein konstanter Wert, der ungleich Null ist.

V. Das Integral einer algebraischen Summe von Funktionen ist gleich der algebraischen Summe der Integrale dieser Funktionen.

∫(f (x)±g (x)) dx=∫f (x) dx±∫g (x) dx.

VI. Wenn F (x) eine Stammfunktion von f (x) ist, und k Und B sind konstante Werte und k≠0, dann ist (1/k)·F (kx+b) eine Stammfunktion für f (kx+b). Tatsächlich gilt nach der Regel zur Berechnung der Ableitung einer komplexen Funktion:

Du kannst schreiben:

Zu jeder mathematischen Aktion gibt es eine umgekehrte Aktion. Für die Differentiation (Finden von Ableitungen von Funktionen) gibt es auch eine umgekehrte Aktion – die Integration. Durch Integration wird eine Funktion aus ihrer gegebenen Ableitung oder ihrem gegebenen Differential gefunden (rekonstruiert). Die gefundene Funktion wird aufgerufen Stammfunktion.

Definition. Differenzierbare Funktion F(x) heißt Stammfunktion der Funktion f(x) in einem bestimmten Intervall, wenn überhaupt X Aus diesem Intervall gilt folgende Gleichheit: F′(x)=f (x).

Beispiele. Finden Sie Stammfunktionen für die Funktionen: 1) f (x)=2x; 2) f (x)=3cos3x.

1) Da (x²)′=2x, dann ist die Funktion F (x)=x² per Definition eine Stammfunktion der Funktion f (x)=2x.

2) (sin3x)′=3cos3x. Wenn wir f (x)=3cos3x und F (x)=sin3x bezeichnen, dann gilt per Definition einer Stammfunktion: F′(x)=f (x) und daher ist F (x)=sin3x eine Stammfunktion für f ( x)=3cos3x.

Beachten Sie, dass (sin3x +5 )′= 3cos3x, und (sin3x -8,2 )′= 3cos3x, ... V Gesamtansicht kann geschrieben werden: (sin3x +C)′= 3cos3x, Wo MIT- ein konstanter Wert. Diese Beispiele verdeutlichen die Mehrdeutigkeit der Integrationswirkung im Gegensatz zur Differenzierungswirkung, wenn jede differenzierbare Funktion eine einzige Ableitung hat.

Definition. Wenn die Funktion F(x) ist eine Stammfunktion der Funktion f(x) in einem bestimmten Intervall hat die Menge aller Stammfunktionen dieser Funktion die Form:

F(x)+C, wobei C eine beliebige reelle Zahl ist.

Die Menge aller Stammfunktionen F (x) + C der Funktion f (x) im betrachteten Intervall wird als unbestimmtes Integral bezeichnet und mit dem Symbol bezeichnet ∫ (Integralzeichen). Aufschreiben: ∫f (x) dx=F (x)+C.

Ausdruck ∫f(x)dx lauten: „Integral ef von x bis de x.“

f(x)dx- Integrandenausdruck,

f(x)— Integrandenfunktion,

X ist die Integrationsvariable.

F(x)- Stammfunktion einer Funktion f(x),

MIT- ein konstanter Wert.

Nun können die betrachteten Beispiele wie folgt geschrieben werden:

1) ∫ 2xdx=x²+C. 2) ∫ 3cos3xdx=sin3x+C.

Was bedeutet das Zeichen d?

D- Differentialzeichen – hat einen doppelten Zweck: Erstens trennt dieses Vorzeichen den Integranden von der Integrationsvariablen; Zweitens wird alles, was nach diesem Vorzeichen kommt, standardmäßig differenziert und mit dem Integranden multipliziert.

Beispiele. Finden Sie die Integrale: 3) ∫ 2pxdx; 4) ∫ 2pxdp.

3) Nach dem Differentialsymbol D Kosten XX, A R

∫ 2хрdx=рх²+С. Vergleichen Sie mit Beispiel 1).

Machen wir einen Check. F′(x)=(px²+C)′=p·(x²)′+C′=p·2x=2px=f (x).

4) Nach dem Differentialsymbol D Kosten R. Dies bedeutet, dass die Integrationsvariable R und der Multiplikator X sollte als ein konstanter Wert betrachtet werden.

∫ 2хрдр=р²х+С. Vergleichen Sie mit Beispielen 1) Und 3).

Machen wir einen Check. F′(p)=(p²x+C)′=x·(p²)′+C′=x·2p=2px=f (p).

Seite 1 von 1 1