Das System der Ungleichheiten Es ist üblich, jede Menge von zwei oder mehr Ungleichungen zu nennen, die eine unbekannte Größe enthalten.

Diese Formulierung wird beispielsweise durch solche deutlich veranschaulicht Ungleichheitssysteme:

Lösen Sie das System der Ungleichungen - bedeutet, alle Werte der unbekannten Variablen zu finden, für die jede Ungleichung des Systems realisiert ist, oder zu beweisen, dass es keine solchen gibt .

Also für jeden Einzelnen Systemungleichheiten Berechnen Sie die unbekannte Variable. Wählt außerdem aus den resultierenden Werten nur diejenigen aus, die sowohl für die erste als auch für die zweite Ungleichung wahr sind. Wenn man also den gewählten Wert einsetzt, werden beide Ungleichungen des Systems richtig.

Lassen Sie uns die Lösung mehrerer Ungleichungen analysieren:

Platzieren Sie eine unter dem anderen Zahlenlinienpaar. Tragen Sie den Wert oben ein X, unter der die erste Ungleichung o ( X> 1) wird wahr und unten der Wert X, die die Lösung der zweiten Ungleichung sind ( X> 4).

Durch den Vergleich der Daten auf Zahlenlinien Beachten Sie, dass die Lösung für beides gilt Ungleichheiten Wille X> 4. Antwort, X> 4.

Beispiel 2

Berechnen des ersten Ungleichheit wir bekommen -3 X< -6, или X> 2, die zweite - X> -8, oder X < 8. Затем делаем по аналогии с предыдущим примером. На верхнюю числовую прямую наносим все те значения X, unter dem der erste Systemungleichheit und auf dem unteren Zahlenstrahl alle diese Werte X, unter der die zweite Ungleichung des Systems realisiert wird.

Beim Vergleich der Daten stellen wir fest, dass beides der Fall ist Ungleichheiten wird für alle Werte implementiert X von 2 bis 8 platziert. Wertemengen X bezeichnen doppelte Ungleichheit 2 < X< 8.

Beispiel 3 Lass uns finden

Programm zum Lösen linearer, quadratischer und gebrochene Ungleichungen gibt nicht nur die Antwort auf das Problem, sondern eine detaillierte Lösung mit Erläuterungen, d.h. Zeigt den Lösungsprozess an, um die Kenntnisse in Mathematik und/oder Algebra zu überprüfen.

Wenn außerdem im Prozess der Lösung einer der Ungleichungen beispielsweise Folgendes gelöst werden muss: quadratische Gleichung, dann wird auch die detaillierte Lösung angezeigt (sie ist im Spoiler enthalten).

Dieses Programm kann für Gymnasiasten bei der Vorbereitung nützlich sein Kontrollarbeit, Eltern, die Lösung von Ungleichheiten durch ihre Kinder zu kontrollieren.

Dieses Programm kann für Oberstufenschüler nützlich sein allgemeinbildende Schulen zur Vorbereitung auf Tests und Prüfungen, bei der Prüfung von Kenntnissen vor dem Einheitlichen Staatsexamen, damit Eltern die Lösung vieler Probleme in Mathematik und Algebra kontrollieren können. Oder ist es für Sie vielleicht zu teuer, einen Nachhilfelehrer zu engagieren oder neue Lehrbücher zu kaufen? Oder möchten Sie es einfach so schnell wie möglich erledigen? Hausaufgaben Mathematik oder Algebra? In diesem Fall können Sie auch unsere Programme mit detaillierter Lösung nutzen.

Auf diese Weise können Sie Ihr eigenes Training durchführen und/oder Ihr eigenes Training durchführen jüngere Brüder oder Schwestern, während das Bildungsniveau im Bereich der zu lösenden Aufgaben steigt.

Regeln für die Eingabe von Ungleichungen

Als Variable kann jeder lateinische Buchstabe fungieren.
Zum Beispiel: \(x, y, z, a, b, c, o, p, q \) usw.

Zahlen können als ganze Zahlen oder Brüche eingegeben werden.
Darüber hinaus können Bruchzahlen nicht nur in Form einer Dezimalzahl, sondern auch in Form eines gewöhnlichen Bruchs eingegeben werden.

Regeln für die Eingabe von Dezimalbrüchen.
Bei Dezimalbrüchen kann der Bruchteil der ganzen Zahl entweder durch einen Punkt oder ein Komma getrennt werden.
Sie können beispielsweise eintreten Dezimalzahlen also: 2,5x - 3,5x^2

Regeln für die Eingabe gewöhnlicher Brüche.
Nur eine ganze Zahl kann als Zähler, Nenner und ganzzahliger Teil eines Bruchs fungieren.

Der Nenner darf nicht negativ sein.

Bei der Eingabe eines Zahlenbruchs wird der Zähler durch ein Divisionszeichen vom Nenner getrennt: /
ganzer Teil durch ein kaufmännisches Und vom Bruch getrennt: &
Eingabe: 3&1/3 - 5&6/5J +1/7J^2
Ergebnis: \(3\frac(1)(3) - 5\frac(6)(5) y + \frac(1)(7)y^2 \)

Bei der Eingabe von Ausdrücken können Klammern verwendet werden. In diesem Fall werden beim Lösen der Ungleichung zunächst die Ausdrücke vereinfacht.
Zum Beispiel: 5(a+1)^2+2&3/5+a > 0,6(a-2)(a+3)

Wählen Sie das gewünschte Ungleichheitszeichen und geben Sie die Polynome in die Felder unten ein.

Die erste Ungleichung des Systems.

Klicken Sie auf die Schaltfläche, um den Typ der ersten Ungleichung zu ändern.

> >= < <=

Lösen Sie das System der Ungleichungen

Es wurde festgestellt, dass einige zur Lösung dieser Aufgabe benötigte Skripte nicht geladen wurden und das Programm möglicherweise nicht funktioniert.
Möglicherweise haben Sie AdBlock aktiviert.
Deaktivieren Sie es in diesem Fall und aktualisieren Sie die Seite.

Sie haben JavaScript in Ihrem Browser deaktiviert.
Damit die Lösung angezeigt wird, muss JavaScript aktiviert sein.
Hier finden Sie Anweisungen, wie Sie JavaScript in Ihrem Browser aktivieren.

Weil Es gibt viele Leute, die das Problem lösen möchten, Ihre Anfrage steht in der Warteschlange.
Nach ein paar Sekunden erscheint unten die Lösung.
Bitte warten Sie Sekunde...

Wenn Sie Habe einen Fehler in der Lösung bemerkt, dann können Sie im Feedback-Formular darüber schreiben.
Nicht vergessen Geben Sie an, um welche Aufgabe es sich handelt Du entscheidest was in die Felder eintragen.

Unsere Spiele, Rätsel, Emulatoren:

Ein bisschen Theorie.

Ungleichungssysteme mit einer Unbekannten. Numerische Bereiche

In der 7. Klasse haben Sie sich mit dem Konzept eines Systems vertraut gemacht und gelernt, lineare Gleichungssysteme mit zwei Unbekannten zu lösen. Als nächstes werden Systeme besprochen. Lineare Ungleichungen mit einem Unbekannten. Die Lösungsmengen von Ungleichungssystemen können mithilfe von Intervallen (Intervalle, Halbintervalle, Segmente, Strahlen) geschrieben werden. Außerdem lernen Sie die Notation numerischer Intervalle kennen.

Wenn in den Ungleichungen \(4x > 2000 \) und \(5x \leq 4000 \) die unbekannte Zahl x gleich ist, dann werden diese Ungleichungen zusammen betrachtet und sie bilden ein System von Ungleichungen: $$ \left\ (\begin( array)(l) 4x > 2000 \\ 5x \leq 4000 \end(array)\right.$$

Die geschweifte Klammer zeigt, dass Sie solche Werte von x finden müssen, für die beide Ungleichungen des Systems zu echten numerischen Ungleichungen werden. Dieses System ist ein Beispiel für ein System linearer Ungleichungen mit einer Unbekannten.

Die Lösung eines Ungleichungssystems mit einer Unbekannten ist der Wert der Unbekannten, bei dem sich alle Ungleichungen des Systems in echte numerische Ungleichungen verwandeln. Ein System von Ungleichungen zu lösen bedeutet, alle Lösungen dieses Systems zu finden oder festzustellen, dass es keine gibt.

Die Ungleichungen \(x \geq -2 \) und \(x \leq 3 \) können als doppelte Ungleichung geschrieben werden: \(-2 \leq x \leq 3 \).

Es gibt verschiedene Lösungen für Ungleichungssysteme mit einer Unbekannten Zahlensätze. Diese Sets haben Namen. Auf der reellen Achse wird also die Menge der Zahlen x mit \(-2 \leq x \leq 3 \) durch ein Segment dargestellt, dessen Enden an den Punkten -2 und 3 liegen.

-2

3

Wenn \(a ein Segment ist und mit [a; b] bezeichnet wird

Wenn \(ein Intervall und bezeichnet mit (a; b)

Mengen von Zahlen \(x \), die die Ungleichungen \(a \leq x in Halbintervallen erfüllen und mit [a; b) bzw. (a; b] bezeichnet werden

Es werden Segmente, Intervalle, Halbintervalle und Strahlen genannt numerische Intervalle.

Somit können numerische Intervalle in Form von Ungleichungen angegeben werden.

Eine Lösung für eine Ungleichung mit zwei Unbekannten ist ein Zahlenpaar (x; y), das diese Ungleichung in eine echte numerische Ungleichung umwandelt. Eine Ungleichung zu lösen bedeutet, die Menge aller ihrer Lösungen zu finden. Die Lösungen der Ungleichung x > y sind also beispielsweise Zahlenpaare (5; 3), (-1; -1), da \(5 \geq 3 \) und \(-1 \geq - 1\)

Ungleichheitssysteme lösen

Sie haben bereits gelernt, wie man lineare Ungleichungen mit einer Unbekannten löst. Wissen, was ein System von Ungleichheiten und eine Lösung für das System ist. Daher wird Ihnen die Lösung von Ungleichungssystemen mit einer Unbekannten keine Schwierigkeiten bereiten.

Und doch erinnern wir uns: Um ein System von Ungleichungen zu lösen, muss man jede Ungleichung einzeln lösen und dann den Schnittpunkt dieser Lösungen finden.

Beispielsweise wurde das ursprüngliche Ungleichungssystem auf die Form reduziert:
$$ \left\(\begin(array)(l) x \geq -2 \\ x \leq 3 \end(array)\right. $$

Um dieses Ungleichungssystem zu lösen, markieren Sie die Lösung jeder Ungleichung auf der reellen Achse und ermitteln Sie deren Schnittpunkt:

-2

3

Der Schnittpunkt ist das Segment [-2; 3] - das ist die Lösung des ursprünglichen Ungleichungssystems.

Ungleichheitslösung im Modus online Lösung fast jede gegebene Ungleichheit online. Mathematisch Ungleichheiten online Mathe lösen. Schnell finden Ungleichheitslösung im Modus online. Die Website www.site ermöglicht es Ihnen, zu finden Lösung fast beliebig algebraisch, trigonometrisch oder Transzendente Ungleichheit online. Beim Studium nahezu aller Zweige der Mathematik unterschiedliche Bühnen muss entscheiden Ungleichheiten online. Um sofort eine Antwort und vor allem eine genaue Antwort zu erhalten, benötigen Sie eine Ressource, die Ihnen dies ermöglicht. Danke an www.site Ungleichheit online lösen wird ein paar Minuten dauern. Der Hauptvorteil von www.site beim Lösen mathematischer Probleme Ungleichheiten online- ist die Geschwindigkeit und Genauigkeit der ausgegebenen Antwort. Die Seite ist in der Lage, jedes Problem zu lösen Algebraische Ungleichungen online, trigonometrische Ungleichungen online, Transzendentale Ungleichheiten online, und auch Ungleichheiten mit unbekannten Parametern im Modus online. Ungleichheiten dienen als leistungsstarker mathematischer Apparat Lösungen praktische Aufgaben. Mit Hilfe mathematische Ungleichungen Es ist möglich, Sachverhalte und Zusammenhänge auszudrücken, die auf den ersten Blick verwirrend und komplex erscheinen könnten. unbekannte Mengen Ungleichheiten kann gefunden werden, indem man das Problem in formuliert mathematisch Sprache im Formular Ungleichheiten Und entscheiden die empfangene Aufgabe im Modus online auf der Website www.site. Beliebig algebraische Ungleichung, trigonometrische Ungleichung oder Ungleichheiten enthaltend transzendental bietet Ihnen ganz einfach entscheiden online und erhalten Sie die richtige Antwort. Beim Studium der Naturwissenschaften stößt man unweigerlich auf die Notwendigkeit Lösung von Ungleichungen. In diesem Fall muss die Antwort korrekt sein und sofort im Modus empfangen werden online. Daher z Lösen Sie mathematische Ungleichungen online Wir empfehlen die Website www.site, die zu Ihrem unverzichtbaren Rechner wird Lösen Sie algebraische Ungleichungen online, trigonometrische Ungleichungen online, und auch Transzendentale Ungleichheiten online oder Ungleichheiten mit unbekannten Parametern. Für praktische Probleme beim Finden von Intravol-Lösungen verschiedener mathematische Ungleichungen Ressource www.. Lösen Ungleichheiten online Für sich selbst ist es sinnvoll, die erhaltene Antwort mit zu überprüfen Online-Lösung Ungleichheiten auf der Website www.site. Es ist notwendig, die Ungleichung richtig aufzuschreiben und sofort zu erhalten Online-Lösung Danach müssen Sie nur noch die Antwort mit Ihrer Lösung der Ungleichung vergleichen. Die Überprüfung der Antwort dauert nicht länger als eine Minute Ungleichheit online lösen und Antworten vergleichen. Dies wird Ihnen helfen, Fehler zu vermeiden Entscheidung und korrigieren Sie die Antwort rechtzeitig Ungleichheiten online lösen entweder algebraisch, trigonometrisch, transzendent oder Ungleichheit mit unbekannten Parametern.

Eine Ungleichung sind zwei Zahlen oder mathematische Ausdrücke, die durch eines der folgenden Zeichen verbunden sind: > (mehr, bei strengen Ungleichungen),< (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).

Ungleichheit ist linear unter den gleichen Bedingungen wie eine Gleichung: Sie enthält nur Variablen ersten Grades und keine Produkte von Variablen.

Die Lösung linearer Ungleichungen und Systeme linearer Ungleichungen ist untrennbar mit ihrer geometrischen Bedeutung verbunden: Die Lösung einer linearen Ungleichung ist eine bestimmte Halbebene, in die die gesamte Ebene durch eine Gerade geteilt wird, deren Gleichung gegeben ist durch eine lineare Ungleichung. Diese Halbebene und im Falle eines Systems linearer Ungleichungen ein durch mehrere Geraden begrenzter Teil der Ebene muss in der Zeichnung gefunden werden.

Viele wirtschaftliche Probleme reduzieren sich auf die Lösung linearer Ungleichungssysteme mit einer großen Anzahl von Variablen, insbesondere lineare Programmierprobleme, bei denen es darum geht, das Maximum oder Minimum einer Funktion zu finden.

Lösen von Systemen linearer Ungleichungen mit beliebig vielen Unbekannten

Lassen Sie uns zunächst lineare Ungleichungen in der Ebene analysieren. Betrachten Sie eine Ungleichung mit zwei Variablen und:

,

Wo sind die Koeffizienten der Variablen (einige Zahlen), ist der freie Term (auch einige Zahlen).

Eine Ungleichung mit zwei Unbekannten hat wie eine Gleichung unendlich viele Lösungen. Eine Lösung für diese Ungleichung ist ein Zahlenpaar, das diese Ungleichung erfüllt. Geometrisch wird die Lösungsmenge der Ungleichung als eine durch eine Gerade begrenzte Halbebene dargestellt

,

die wir Grenzlinie nennen werden.

Schritt 1. Konstruieren Sie eine gerade Linie, die die Lösungsmenge der linearen Ungleichung begrenzt

Dazu müssen Sie zwei beliebige Punkte dieser Geraden kennen. Finden wir die Schnittpunkte mit den Koordinatenachsen. Schnittpunkt-Ordinate A ist Null (Abbildung 1). Die Zahlenwerte auf den Achsen in dieser Abbildung beziehen sich auf Beispiel 1, das wir gleich im Anschluss an diesen theoretischen Exkurs analysieren werden.

Wir finden die Abszisse, indem wir die Gleichung einer Geraden mit der Achsengleichung als System lösen.

Finden wir den Schnittpunkt mit der Achse:

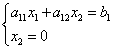
Wenn wir den Wert in die erste Gleichung einsetzen, erhalten wir

Wo .

Somit haben wir die Abszisse des Punktes gefunden A .

Finden wir die Koordinaten des Schnittpunkts mit der Achse.

Abszissenpunkt B gleich Null. Lösen wir die Gleichung der Grenzlinie mit der Gleichung der Koordinatenachse:

,

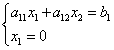
daher die Koordinaten des Punktes B: .

Schritt 2. Zeichnen Sie eine Linie, die die Lösungsmenge der Ungleichung begrenzt. Die Punkte kennen A Und B Schnittpunkt der Grenzlinie mit den Koordinatenachsen, können wir diese Linie zeichnen. Die Gerade (wieder Abbildung 1) teilt die gesamte Ebene in zwei Teile, die rechts und links (oben und unten) dieser Geraden liegen.

Schritt 3. Bestimmen Sie, welche der Halbebenen die Lösung dieser Ungleichung ist. Dazu müssen wir den Koordinatenursprung (0; 0) in diese Ungleichung einsetzen. Wenn die Koordinaten des Ursprungs die Ungleichung erfüllen, ist die Lösung der Ungleichung die Halbebene, in der sich der Ursprung befindet. Wenn die Koordinaten die Ungleichung nicht erfüllen, ist die Lösung der Ungleichung eine Halbebene, die den Ursprung nicht enthält. Die Halbebene der Lösung der Ungleichung wird durch Striche von der Geraden innerhalb der Halbebene gekennzeichnet, wie in Abbildung 1.

Wenn wir das System der linearen Ungleichungen lösen, dann wird jeder Schritt für jede der Ungleichungen des Systems ausgeführt.

Beispiel 1 Lösen Sie die Ungleichung

Lösung. Zeichnen wir eine gerade Linie

Wenn wir eine Gerade in die Gleichung einsetzen, erhalten wir, und wenn wir sie einsetzen, erhalten wir. Daher sind die Koordinaten der Schnittpunkte mit den Achsen A(3; 0) , B(0; 2) . Zeichnen Sie eine gerade Linie durch diese Punkte (wiederum Abbildung 1).

Wir wählen eine Halbebene von Lösungen für die Ungleichung. Dazu setzen wir die Koordinaten des Anfangs (0; 0) in die Ungleichung ein:

wir erhalten , d. h. die Koordinaten des Ursprungs erfüllen diese Ungleichung. Folglich ist die Lösung der Ungleichung eine Halbebene, die den Ursprung enthält, d. h. die linke (oder untere) Halbebene.

Wenn diese Ungleichung streng wäre, hätte sie die Form

dann wären die Punkte der Grenzlinie keine Lösung, da sie die Ungleichung nicht erfüllen.

Betrachten Sie nun ein System linearer Ungleichungen mit zwei Unbekannten:

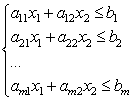
Jede der Ungleichungen dieses Systems auf der Ebene definiert eine Halbebene. Ein System linearer Ungleichungen heißt konsistent, wenn es mindestens eine Lösung hat, und inkonsistent, wenn es keine Lösungen hat. Eine Lösung für ein System linearer Ungleichungen ist jedes Zahlenpaar (), das alle Ungleichungen dieses Systems erfüllt.

Geometrisch gesehen ist die Lösung eines Systems linearer Ungleichungen die Menge der Punkte, die alle Ungleichungen des Systems erfüllen, also der gemeinsame Teil der resultierenden Halbebenen. Daher kann die Lösung geometrisch im Allgemeinen als ein bestimmtes Polygon dargestellt werden, im Einzelfall kann es sich um eine Linie, ein Segment und sogar einen Punkt handeln. Wenn das System linearer Ungleichungen inkonsistent ist, gibt es keinen einzigen Punkt auf der Ebene, der alle Ungleichungen des Systems erfüllt.

Beispiel 2

Lösung. Es ist also erforderlich, ein Lösungspolygon dieses Ungleichungssystems zu finden. Konstruieren wir eine Grenzlinie für die erste Ungleichung, also eine Gerade, und eine Grenzlinie für die zweite Ungleichung, also eine Gerade.

Dies tun wir schrittweise, wie in der theoretischen Referenz und in Beispiel 1 gezeigt wurde, zumal in Beispiel 1 eine Grenzlinie für die Ungleichung gebildet wurde, die die erste in diesem System ist.

Die den Ungleichungen dieses Systems entsprechenden Lösungshalbebenen sind in Abbildung 2 nach innen schattiert. Der gemeinsame Teil der Lösungshalbebenen ist ein offener Winkel ABC. Dies bedeutet, dass die Menge der Punkte in der Ebene, die den offenen Winkel bilden ABC ist eine Lösung sowohl für die erste als auch für die zweite Ungleichung des Systems, also eine Lösung für ein System aus zwei linearen Ungleichungen. Mit anderen Worten, die Koordinaten eines beliebigen Punktes aus dieser Menge erfüllen beide Ungleichungen des Systems.

Beispiel 3 Lösen Sie ein System linearer Ungleichungen

Lösung. Konstruieren wir die Grenzlinien, die den Ungleichungen des Systems entsprechen. Wir tun dies, indem wir die im theoretischen Hintergrund für jede Ungleichung angegebenen Schritte befolgen. Jetzt definieren wir die Halbebenen der Lösungen für jede Ungleichung (Abbildung 3).

Die den Ungleichungen des gegebenen Systems entsprechenden Lösungshalbebenen sind nach innen schattiert. Der Schnittpunkt der Halbebenen der Lösungen wird, wie in der Abbildung dargestellt, in Form eines Vierecks dargestellt ABCE. Wir haben herausgefunden, dass das Lösungspolygon eines Systems linearer Ungleichungen mit zwei Variablen ein Viereck ist ABCE .

Alles, was oben über Systeme linearer Ungleichungen mit zwei Unbekannten beschrieben wurde, gilt auch für ein System von Ungleichungen mit beliebig vielen Unbekannten, mit dem einzigen Unterschied, dass die Lösung einer Ungleichung mit N das Unbekannte wird die Gesamtheit sein N Zahlen (), die alle Ungleichungen erfüllen, und anstelle der Grenzlinie wird es eine Grenzhyperebene geben N-dimensionaler Raum. Die Lösung wird ein durch Hyperebenen begrenztes Lösungspolyeder (Simplex) sein.

siehe auch Ein lineares Programmierproblem grafisch lösen, Kanonische Form linearer Programmierprobleme

Das System der Beschränkungen für ein solches Problem besteht aus Ungleichungen in zwei Variablen:
und die Zielfunktion hat die Form F = C 1 X + C 2 j, die maximiert werden soll.

Beantworten wir die Frage: Welche Zahlenpaare ( X; j) sind Lösungen für das System der Ungleichungen, d. h. erfüllen sie alle Ungleichungen gleichzeitig? Mit anderen Worten: Was bedeutet es, ein System grafisch zu lösen?
Zuerst müssen Sie verstehen, was die Lösung einer linearen Ungleichung mit zwei Unbekannten ist.
Eine lineare Ungleichung mit zwei Unbekannten zu lösen bedeutet, alle Wertepaare der Unbekannten zu bestimmen, für die die Ungleichung erfüllt ist.
Zum Beispiel Ungleichung 3 X – 5j≥ 42 erfüllen die Paare ( X , j) : (100, 2); (3, –10) usw. Das Problem besteht darin, alle solchen Paare zu finden.
Betrachten Sie zwei Ungleichungen: Axt + von≤ C, Axt + von≥ C. Gerade Axt + von = C teilt die Ebene in zwei Halbebenen, sodass die Koordinaten der Punkte einer von ihnen die Ungleichung erfüllen Axt + von >C und die andere Ungleichung Axt + +von <C.
Nehmen Sie tatsächlich einen Punkt mit Koordinaten X = X 0; dann ein Punkt, der auf einer Geraden liegt und eine Abszisse hat X 0 hat eine Ordinate

Lassen Sie es zur Bestimmtheit A<0, B>0, C>0. Alle Punkte mit Abszisse X 0 oben P(z. B. Punkt M), haben y M>j 0 und alle Punkte unterhalb des Punktes P, mit Abszisse X 0 , haben yN<j 0 . Weil das X 0 ist ein beliebiger Punkt, dann wird es immer Punkte auf einer Seite der Linie geben, für die Axt+ von > C, eine Halbebene bildend, und andererseits Punkte für welche Axt + von< C.

Bild 1

Das Ungleichheitszeichen in der Halbebene hängt von den Zahlen ab A, B , C.
Dies impliziert die folgende Methode zur grafischen Lösung von Systemen linearer Ungleichungen in zwei Variablen. Um das System zu lösen, benötigen Sie:

1. Schreiben Sie für jede Ungleichung die Gleichung auf, die der gegebenen Ungleichung entspricht.
2. Konstruieren Sie Linien, die Graphen von durch Gleichungen gegebenen Funktionen sind.
3. Bestimmen Sie für jede Gerade die Halbebene, die durch die Ungleichung gegeben ist. Nehmen Sie dazu einen beliebigen Punkt, der nicht auf einer Geraden liegt, und setzen Sie seine Koordinaten in die Ungleichung ein. Wenn die Ungleichung wahr ist, ist die Halbebene, die den gewählten Punkt enthält, die Lösung der ursprünglichen Ungleichung. Wenn die Ungleichung falsch ist, dann ist die Halbebene auf der anderen Seite der Linie die Lösungsmenge dieser Ungleichung.
4. Um ein System von Ungleichungen zu lösen, ist es notwendig, die Schnittfläche aller Halbebenen zu finden, die die Lösung für jede Ungleichung im System darstellen.

Dieser Bereich kann sich als leer erweisen, dann hat das Ungleichheitssystem keine Lösungen, es ist inkonsistent. Ansonsten gilt das System als konsistent.
Lösungen können eine endliche Zahl und eine unendliche Menge sein. Die Fläche kann ein geschlossenes Polygon sein oder unbegrenzt sein.

Schauen wir uns drei relevante Beispiele an.

Beispiel 1. Lösen Sie das System grafisch:
X + y- 1 ≤ 0;
–2X- 2j + 5 ≤ 0.

• Betrachten Sie die Gleichungen x+y–1=0 und –2x–2y+5=0, die den Ungleichungen entsprechen;
• Konstruieren wir die durch diese Gleichungen gegebenen Geraden.

Figur 2

Definieren wir die durch die Ungleichungen gegebenen Halbebenen. Nehmen Sie einen beliebigen Punkt, seien Sie (0; 0). In Betracht ziehen X+ y– 1 0, wir ersetzen den Punkt (0; 0): 0 + 0 – 1 ≤ 0. Daher gilt in der Halbebene, in der der Punkt (0; 0) liegt, X + j – 1 ≤ 0, d.h. Die unter der Geraden liegende Halbebene ist die Lösung der ersten Ungleichung. Wenn wir diesen Punkt (0; 0) in den zweiten einsetzen, erhalten wir: –2 ∙ 0 – 2 ∙ 0 + 5 ≤ 0, d. h. in der Halbebene, in der der Punkt (0; 0) liegt, -2 X – 2j+ 5≥ 0, und wir wurden gefragt, wo -2 X – 2j+ 5 ≤ 0 also in einer anderen Halbebene – in der über der Geraden.
Finden Sie den Schnittpunkt dieser beiden Halbebenen. Die Geraden sind parallel, die Ebenen schneiden sich also nirgendwo, was bedeutet, dass das System dieser Ungleichungen keine Lösungen hat, es ist inkonsistent.

Beispiel 2. Finden Sie grafisch Lösungen für das Ungleichungssystem:

Figur 3
1. Schreiben Sie die Gleichungen auf, die den Ungleichungen entsprechen, und konstruieren Sie Geraden.
X + 2j– 2 = 0

X	2	0
j	0	1

j – X – 1 = 0

X	0	2
j	1	3

j + 2 = 0;
j = –2.
2. Nachdem wir den Punkt (0; 0) gewählt haben, bestimmen wir die Vorzeichen der Ungleichungen in den Halbebenen:
0 + 2 ∙ 0 – 2 ≤ 0, d.h. X + 2j– 2 ≤ 0 in der Halbebene unterhalb der Geraden;
0 – 0 – 1 ≤ 0, d.h. j –X– 1 ≤ 0 in der Halbebene unterhalb der Geraden;
0 + 2 =2 ≥ 0, d.h. j+ 2 ≥ 0 in der Halbebene über der Linie.
3. Der Schnittpunkt dieser drei Halbebenen ergibt eine Fläche, die einem Dreieck entspricht. Es ist nicht schwierig, die Eckpunkte der Region als Schnittpunkte der entsprechenden Linien zu finden


Auf diese Weise, A(–3; –2), IN(0; 1), MIT(6; –2).

Betrachten wir ein weiteres Beispiel, bei dem der resultierende Lösungsbereich des Systems nicht eingeschränkt ist.