Sistemul inegalităților Se obișnuiește să se numească orice set de două sau mai multe inegalități care conțin o cantitate necunoscută.

Această formulare este ilustrată în mod clar, de exemplu, de astfel sisteme de inegalităţi:

Rezolvați sistemul de inegalități - înseamnă a găsi toate valorile variabilei necunoscute pentru care se realizează fiecare inegalitate a sistemului sau a demonstra că nu există astfel de .

Deci, pentru fiecare individ inegalități de sistem calculați variabila necunoscută. În plus, din valorile rezultate, le selectează numai pe cele care sunt adevărate atât pentru prima cât și pentru a doua inegalități. Prin urmare, la înlocuirea valorii alese, ambele inegalități ale sistemului devin corecte.

Să analizăm soluția mai multor inegalități:

Plasați unul sub cealaltă pereche de linii numerice; pune valoarea pe partea de sus X, sub care prima inegalitate o ( X> 1) devin adevărate, iar în partea de jos, valoarea X, care sunt soluția celei de-a doua inegalități ( X> 4).

Prin compararea datelor de pe linii numerice, rețineți că soluția pentru ambele inegalităților va fi X> 4. Răspunde, X> 4.

Exemplul 2

Calculând primul inegalitate obținem -3 X< -6, или X> 2, al doilea - X> -8 sau X < 8. Затем делаем по аналогии с предыдущим примером. На верхнюю числовую прямую наносим все те значения X, sub care primul inegalitatea sistemului, iar pe linia numerică inferioară, toate acele valori X, sub care se realizează a doua inegalitate a sistemului.

Comparând datele, constatăm că ambele inegalităților va fi implementat pentru toate valorile X plasat de la 2 la 8. Seturi de valori X denota dubla inegalitate 2 < X< 8.

Exemplul 3 Sa gasim

Program pentru rezolvarea liniară, pătrată și inegalități fracționale nu doar dă răspunsul problemei, ci oferă o soluție detaliată cu explicații, adică. afiseaza procesul de rezolvare in vederea verificarii cunostintelor de matematica si/sau algebra.

Mai mult, dacă în procesul de rezolvare a uneia dintre inegalități este necesar să se rezolve, de exemplu, ecuație pătratică, apoi este afișată și soluția sa detaliată (este inclusă în spoiler).

Acest program poate fi util elevilor de liceu în pregătire pentru munca de control, părinții să controleze soluționarea inegalităților de către copiii lor.

Acest program poate fi util elevilor de liceu scoli de invatamant generalîn pregătirea pentru teste și examene, la testarea cunoștințelor înainte de Examenul Unificat de Stat, pentru ca părinții să controleze rezolvarea multor probleme de matematică și algebră. Sau poate este prea scump pentru tine să angajezi un tutor sau să cumperi noi manuale? Sau vrei doar să o faci cât mai curând posibil? teme pentru acasă matematica sau algebra? În acest caz, puteți folosi și programele noastre cu o soluție detaliată.

În acest fel, vă puteți conduce propriul antrenament și/sau vă puteți antrena frati mai mici sau surori, în timp ce nivelul de educație în domeniul sarcinilor în curs de rezolvare crește.

Reguli pentru introducerea inegalităților

Orice literă latină poate acționa ca o variabilă.
De exemplu: \(x, y, z, a, b, c, o, p, q \) etc.

Numerele pot fi introduse ca numere întregi sau fracții.
Mai mult, numerele fracționale pot fi introduse nu numai sub forma unei zecimale, ci și sub forma unei fracții obișnuite.

Reguli pentru introducerea fracțiilor zecimale.
În fracțiile zecimale, partea fracțională din întreg poate fi separată fie prin punct, fie prin virgulă.
De exemplu, puteți intra zecimale deci: 2,5x - 3,5x^2

Reguli pentru introducerea fracțiilor obișnuite.
Doar un număr întreg poate acționa ca numărător, numitor și parte întreagă a unei fracții.

Numitorul nu poate fi negativ.

Când introduceți o fracție numerică, numărătorul este separat de numitor printr-un semn de împărțire: /
întreaga parte separate de fracție printr-un ampersand: &
Intrare: 3&1/3 - 5&6/5y +1/7y^2
Rezultat: \(3\frac(1)(3) - 5\frac(6)(5) y + \frac(1)(7)y^2 \)

Parantezele pot fi folosite la introducerea expresiilor. În acest caz, la rezolvarea inegalității, expresiile sunt mai întâi simplificate.
De exemplu: 5(a+1)^2+2&3/5+a > 0,6(a-2)(a+3)

Alegeți semnul de inegalitate dorit și introduceți polinoamele în câmpurile de mai jos.

Prima inegalitate a sistemului.

Faceți clic pe butonul pentru a schimba tipul primei inegalități.

> >= < <=

Rezolvați sistemul de inegalități

S-a constatat că unele scripturi necesare pentru a rezolva această sarcină nu au fost încărcate și este posibil ca programul să nu funcționeze.
Este posibil să aveți AdBlock activat.
În acest caz, dezactivați-l și reîmprospătați pagina.

Aveți JavaScript dezactivat în browser.
JavaScript trebuie să fie activat pentru ca soluția să apară.
Iată instrucțiuni despre cum să activați JavaScript în browserul dvs.

pentru că Sunt o mulțime de oameni care doresc să rezolve problema, cererea ta este pusă în coadă.
După câteva secunde, soluția va apărea mai jos.
Asteapta te rog sec...

daca tu observat o eroare în soluție, apoi puteți scrie despre asta în Formularul de feedback .
Nu uita indicați ce sarcină tu decizi ce intra in campuri.

Jocurile, puzzle-urile, emulatorii noștri:

Un pic de teorie.

Sisteme de inegalități cu o necunoscută. Intervalele numerice

Te-ai familiarizat cu conceptul de sistem în clasa a VII-a și ai învățat cum să rezolvi sisteme de ecuații liniare cu două necunoscute. Sistemele vor fi discutate în continuare. inegalități liniare cu unul necunoscut. Seturile de soluții ale sistemelor de inegalități pot fi scrise folosind intervale (intervale, semiintervale, segmente, raze). Veți învăța și despre notarea intervalelor numerice.

Dacă în inegalitățile \(4x > 2000 \) și \(5x \leq 4000 \) numărul necunoscut x este același, atunci aceste inegalități sunt considerate împreună și se spune că formează un sistem de inegalități: $$ \left\ (\begin( array)(l) 4x > 2000 \\ 5x \leq 4000 \end(array)\right.$$

Acolada arată că trebuie să găsiți astfel de valori ale lui x pentru care ambele inegalități ale sistemului se transformă în inegalități numerice adevărate. Acest sistem este un exemplu de sistem de inegalități liniare cu o necunoscută.

Soluția unui sistem de inegalități cu o necunoscută este valoarea necunoscutului la care toate inegalitățile sistemului se transformă în inegalități numerice adevărate. A rezolva un sistem de inegalități înseamnă a găsi toate soluțiile acestui sistem sau a stabili că nu există.

Inegalitățile \(x \geq -2 \) și \(x \leq 3 \) pot fi scrise ca o dublă inegalitate: \(-2 \leq x \leq 3 \).

Soluțiile la sistemele de inegalități cu o necunoscută sunt diverse seturi de numere. Aceste seturi au nume. Deci, pe axa reală, mulțimea numerelor x astfel încât \(-2 \leq x \leq 3 \) este reprezentată de un segment cu capete în punctele -2 și 3.

-2

3

Dacă \(a este un segment și este notat cu [a; b]

Dacă \(un interval și notat cu (a; b)

Mulțimi de numere \(x \) care satisfac inegalitățile \(a \leq x prin semiintervale și sunt notate cu [a; b) și respectiv (a; b]

Se numesc segmente, intervale, semiintervale și raze intervale numerice.

Astfel, intervalele numerice pot fi specificate sub formă de inegalități.

O soluție a unei inegalități cu două necunoscute este o pereche de numere (x; y) care transformă această inegalitate într-o inegalitate numerică adevărată. A rezolva o inegalitate înseamnă a găsi mulțimea tuturor soluțiilor ei. Deci, soluțiile inegalității x > y vor fi, de exemplu, perechi de numere (5; 3), (-1; -1), deoarece \(5 \geq 3 \) și \(-1 \geq - 1\)

Rezolvarea sistemelor de inegalități

Ați învățat deja cum să rezolvați inegalitățile liniare cu o necunoscută. Aflați ce sunt un sistem de inegalități și o soluție a sistemului. Prin urmare, procesul de rezolvare a sistemelor de inegalități cu o necunoscută nu vă va provoca dificultăți.

Și totuși ne amintim: pentru a rezolva un sistem de inegalități, trebuie să rezolvați fiecare inegalitate separat și apoi să găsiți intersecția acestor soluții.

De exemplu, sistemul original de inegalități a fost redus la forma:
$$ \left\(\begin(array)(l) x \geq -2 \\ x \leq 3 \end(array)\right. $$

Pentru a rezolva acest sistem de inegalități, marcați soluția fiecărei inegalități pe axa reală și găsiți intersecția lor:

-2

3

Intersecția este segmentul [-2; 3] - aceasta este soluția sistemului original de inegalități.

solutie inegalitatiiîn mod pe net soluţie aproape orice inegalitate dată pe net. Matematic inegalități online pentru a rezolva matematica. Găsiți repede solutie inegalitatiiîn mod pe net. Site-ul www.site vă permite să găsiți soluţie aproape orice dat algebric, trigonometric sau inegalitate transcendentă online. Când studiezi aproape orice ramură a matematicii pe diferite etape trebuie să decidă inegalități online. Pentru a obține un răspuns imediat și, cel mai important, un răspuns precis, aveți nevoie de o resursă care vă permite să faceți acest lucru. Multumesc www.site rezolva inegalitatea online va dura câteva minute. Principalul avantaj al www.site-ului atunci când rezolvăm matematică inegalități online- este viteza și acuratețea răspunsului emis. Site-ul este capabil să rezolve orice inegalități algebrice online, inegalități trigonometrice online, inegalități transcendentale online, precum și inegalităților cu parametri necunoscuți în modul pe net. inegalităților servesc ca un puternic aparat matematic solutii sarcini practice. Cu ajutor inegalități matematice este posibil să se exprime fapte și relații care pot părea la prima vedere confuze și complexe. cantități necunoscute inegalităților poate fi găsit prin formularea problemei în matematic limba în formă inegalitățilorși decide sarcina primită în modul pe net pe site-ul www.site. Orice inegalitatea algebrică, inegalitatea trigonometrică sau inegalităților conținând transcendental te prezintă cu ușurință decide online și obțineți răspunsul corect. Studiind științele naturii, se întâlnește inevitabil nevoia rezolvarea inegalităților. În acest caz, răspunsul trebuie să fie corect și trebuie primit imediat în modul pe net. Prin urmare, pentru Rezolvarea inegalităților matematice online vă recomandăm site-ul www.site, care va deveni calculatorul dumneavoastră indispensabil pentru rezolvarea inegalităților algebrice online, inegalități trigonometrice online, precum și inegalități transcendentale online sau inegalităților cu parametri necunoscuți. Pentru probleme practice de găsire a soluţiilor intravol de diverse inegalități matematice resursa www.. Rezolvarea inegalități online singur, este util să verificați răspunsul primit folosind soluție online inegalităților pe site-ul www.site. Este necesar să notați corect inegalitatea și să obțineți instantaneu soluție online, după care rămâne doar să comparăm răspunsul cu soluția ta la inegalitate. Verificarea răspunsului nu va dura mai mult de un minut, suficient rezolva inegalitatea onlineși comparați răspunsurile. Acest lucru vă va ajuta să evitați greșelile în decizie si corecteaza raspunsul la timp rezolvarea inegalităților online dacă algebric, trigonometric, transcendent sau inegalitate cu parametri necunoscuți.

O inegalitate este două numere sau expresii matematice legate prin unul dintre semnele: > (mai mult, în cazul inegalităților stricte),< (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).

inegalitatea este liniarîn aceleaşi condiţii ca o ecuaţie: conţine variabile doar până la gradul I şi nu conţine produse ale variabilelor.

Soluția inegalităților liniare și a sistemelor de inegalități liniare este indisolubil legată de semnificația lor geometrică: soluția unei inegalități liniare este un anumit semiplan, în care întregul plan este împărțit printr-o dreaptă, a cărei ecuație este dată de o inegalitate liniară. Acest semiplan și, în cazul unui sistem de inegalități liniare, o parte a planului mărginită de mai multe drepte, trebuie găsite în desen.

Multe probleme economice se reduc la rezolvarea sistemelor de inegalități liniare cu un număr mare de variabile, în special, a problemelor de programare liniară în care se cere găsirea maximului sau minimului unei funcții.

Rezolvarea sistemelor de inegalități liniare cu orice număr de necunoscute

Să analizăm mai întâi inegalitățile liniare în plan. Se consideră o inegalitate cu două variabile și:

,

unde sunt coeficienții variabilelor (unele numere), este termenul liber (și un număr).

O inegalitate cu două necunoscute, ca o ecuație, are un număr infinit de soluții. O soluție a acestei inegalități este o pereche de numere care satisfac această inegalitate. Din punct de vedere geometric, setul de soluții ale inegalității este reprezentat ca un semiplan delimitat de o linie dreaptă

,

pe care o vom numi linia de hotar.

Pasul 1. Construiți o dreaptă care mărginește mulțimea soluțiilor inegalității liniare

Pentru a face acest lucru, trebuie să cunoașteți oricare două puncte ale acestei linii. Să găsim punctele de intersecție cu axele de coordonate. ordonata de intersectie A este zero (Figura 1). Valorile numerice de pe axele din această figură se referă la exemplul 1, pe care îl vom analiza imediat după această digresiune teoretică.

Găsim abscisa rezolvând ca sistem ecuația unei drepte cu ecuația axei.

Să găsim intersecția cu axa:

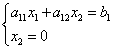
Înlocuind valoarea în prima ecuație, obținem

Unde .

Astfel, am găsit abscisa punctului A .

Să găsim coordonatele punctului de intersecție cu axa.

Punct de abscisă B este egal cu zero. Să rezolvăm ecuația liniei de limită cu ecuația axei de coordonate:

,

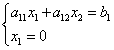
de unde coordonatele punctului B: .

Pasul 2. Desenați o linie care delimitează setul de soluții ale inegalității. Cunoscând punctele Ași B intersectia liniei de limita cu axele de coordonate, putem trasa aceasta linie. Linia dreaptă (din nou figura 1) împarte întregul plan în două părți situate la dreapta și la stânga (deasupra și dedesubt) acestei linii drepte.

Pasul 3. Determinați care dintre semiplanuri este soluția acestei inegalități. Pentru a face acest lucru, trebuie să înlocuim originea coordonatelor (0; 0) în această inegalitate. Dacă coordonatele originii satisfac inegalitatea, atunci soluția inegalității este semiplanul în care se află originea. Dacă coordonatele nu satisfac inegalitatea, atunci soluția inegalității este un semiplan care nu conține originea. Semiplanul soluției inegalității va fi notat cu linii din dreapta din interiorul semiplanului, ca în Figura 1.

Dacă rezolvăm sistemul de inegalități liniare, apoi fiecare pas este efectuat pentru fiecare dintre inegalitățile sistemului.

Exemplul 1 Rezolvați inegalitatea

Soluţie. Să tragem o linie dreaptă

Înlocuind o linie dreaptă în ecuație, obținem, iar înlocuind, obținem. Prin urmare, coordonatele punctelor de intersecție cu axele vor fi A(3; 0) , B(0; 2). Desenați o linie dreaptă prin aceste puncte (din nou, Figura 1).

Alegem un semiplan de soluții ale inegalității. Pentru a face acest lucru, înlocuim coordonatele începutului (0; 0) în inegalitatea:

obținem , adică coordonatele originii satisfac această inegalitate. În consecință, soluția inegalității este un semiplan care conține originea, adică semiplanul stâng (sau inferior).

Dacă această inegalitate ar fi strictă, adică ar avea forma

atunci punctele liniei de frontieră nu ar fi o soluție, deoarece nu satisfac inegalitatea.

Acum luați în considerare un sistem de inegalități liniare cu două necunoscute:

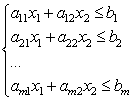
Fiecare dintre inegalitățile acestui sistem pe plan definește un semiplan. Un sistem de inegalități liniare se numește consistent dacă are cel puțin o soluție și inconsecvent dacă nu are soluții. O soluție a unui sistem de inegalități liniare este orice pereche de numere () care satisface toate inegalitățile acestui sistem.

Din punct de vedere geometric, soluția unui sistem de inegalități liniare este mulțimea de puncte care satisfac toate inegalitățile sistemului, adică partea comună a semiplanurilor rezultate. Prin urmare, geometric, în cazul general, soluția poate fi descrisă ca un anumit poligon, într-un caz particular, poate fi o linie, un segment și chiar un punct. Dacă sistemul de inegalități liniare este inconsecvent, atunci nu există un singur punct pe plan care să satisfacă toate inegalitățile sistemului.

Exemplul 2

Soluţie. Deci, este necesar să se găsească un poligon de soluții ale acestui sistem de inegalități. Să construim o linie de limită pentru prima inegalitate, adică o linie, și o linie de limită pentru a doua inegalitate, adică o linie.

Facem acest lucru pas cu pas, așa cum s-a arătat în referința teoretică și în exemplul 1, mai ales că în exemplul 1 a fost construită o linie de frontieră pentru inegalitate, care este prima din acest sistem.

Semiplanurile soluției corespunzătoare inegalităților acestui sistem sunt umbrite spre interior în Figura 2. Partea comună a semiplanurilor soluției este un unghi deschis ABC. Aceasta înseamnă că setul de puncte din plan care formează unghiul deschis ABC, este o soluție atât pentru prima cât și pentru a doua inegalități ale sistemului, adică este o soluție pentru un sistem de două inegalități liniare. Cu alte cuvinte, coordonatele oricărui punct din această mulțime satisfac ambele inegalități ale sistemului.

Exemplul 3 Rezolvați un sistem de inegalități liniare

Soluţie. Să construim liniile de limită corespunzătoare inegalităților sistemului. Facem acest lucru urmând pașii dați în contextul teoretic pentru fiecare inegalitate. Acum definim semiplanurile soluțiilor pentru fiecare inegalitate (Figura 3).

Semiplanurile soluției corespunzătoare inegalităților sistemului dat sunt umbrite spre interior. Intersecția semiplanurilor soluțiilor este reprezentată, așa cum se arată în figură, sub forma unui patrulater ABCE. Am constatat că poligonul soluție al unui sistem de inegalități liniare cu două variabile este un patrulater ABCE .

Tot ceea ce este descris mai sus despre sistemele de inegalități liniare cu două necunoscute se aplică și unui sistem de inegalități cu orice număr de necunoscute, cu singura diferență că soluția unei inegalități cu n necunoscutul va fi totalitatea n numere () care satisfac toate inegalitățile, iar în locul liniei de graniță va exista un hiperplan de graniță n-spațiul dimensional. Soluția va fi un poliedru de soluție (simplex) mărginit de hiperplane.

vezi și Rezolvarea grafică a unei probleme de programare liniară, Forma canonică a problemelor de programare liniară

Sistemul de constrângeri pentru o astfel de problemă constă din inegalități în două variabile:
iar funcţia obiectiv are forma F = C 1 X + C 2 y, care urmează să fie maximizat.

Să răspundem la întrebarea: ce perechi de numere ( X; y) sunt soluții ale sistemului de inegalități, adică satisfac fiecare dintre inegalități simultan? Cu alte cuvinte, ce înseamnă să rezolvi un sistem grafic?
Mai întâi trebuie să înțelegeți care este soluția unei inegalități liniare cu două necunoscute.
A rezolva o inegalitate liniară cu două necunoscute înseamnă a determina toate perechile de valori ale necunoscutelor pentru care inegalitatea este satisfăcută.
De exemplu, inegalitatea 3 X – 5y≥ 42 satisface perechile ( X , y): (100, 2); (3, –10), etc. Problema este de a găsi toate astfel de perechi.
Luați în considerare două inegalități: topor + de≤ c, topor + de≥ c. Drept topor + de = cîmparte planul în două semiplane astfel încât coordonatele punctelor unuia dintre ele să satisfacă inegalitatea topor + de >c, iar cealaltă inegalitate topor + +de <c.
Într-adevăr, luați un punct cu coordonate X = X 0; apoi un punct situat pe o linie dreaptă și având o abscisă X 0 , are o ordonată

Lăsați pentru certitudine A<0, b>0, c>0. Toate punctele cu abscisă X 0 mai sus P(de exemplu, punct M), avea y M>y 0 și toate punctele sub punct P, cu abscisă X 0, au yN<y 0 . Pentru că X 0 este un punct arbitrar, atunci vor exista întotdeauna puncte pe o parte a liniei pentru care topor+ de > c, formând un semiplan, iar pe de altă parte, puncte pentru care topor + de< c.

Poza 1

Semnul de inegalitate în semiplan depinde de numere A, b , c.
Aceasta implică următoarea metodă de rezolvare grafică a sistemelor de inegalități liniare în două variabile. Pentru a rezolva sistemul, aveți nevoie de:

1. Pentru fiecare inegalitate, scrieți ecuația corespunzătoare inegalității date.
2. Construiți drepte care sunt grafice ale funcțiilor date prin ecuații.
3. Pentru fiecare linie dreaptă, determinați semiplanul, care este dat de inegalitate. Pentru a face acest lucru, luați un punct arbitrar care nu se află pe o linie dreaptă, înlocuiți coordonatele sale în inegalitate. dacă inegalitatea este adevărată, atunci semiplanul care conține punctul ales este soluția inegalității inițiale. Dacă inegalitatea este falsă, atunci semiplanul de pe cealaltă parte a dreptei este mulțimea soluțiilor acestei inegalități.
4. Pentru a rezolva un sistem de inegalități, este necesar să găsiți aria de intersecție a tuturor semiplanurilor care sunt soluția fiecărei inegalități din sistem.

Această zonă se poate dovedi goală, atunci sistemul de inegalități nu are soluții, este inconsecvent. În caz contrar, se spune că sistemul este compatibil.
Soluțiile pot fi un număr finit și o mulțime infinită. Zona poate fi un poligon închis sau poate fi nelimitată.

Să ne uităm la trei exemple relevante.

Exemplul 1. Rezolvați grafic sistemul:
X + y- 1 ≤ 0;
–2X- 2y + 5 ≤ 0.

• se consideră ecuațiile x+y–1=0 și –2x–2y+5=0 corespunzătoare inegalităților;
• să construim drepte date de aceste ecuații.

Figura 2

Să definim semiplanurile date de inegalități. Luați un punct arbitrar, fie (0; 0). Considera X+ y– 1 0, înlocuim punctul (0; 0): 0 + 0 – 1 ≤ 0. prin urmare, în semiplanul în care se află punctul (0; 0), X + y – 1 ≤ 0, adică semiplanul situat sub linia dreaptă este soluția primei inegalități. Înlocuind acest punct (0; 0) în al doilea, obținem: –2 ∙ 0 – 2 ∙ 0 + 5 ≤ 0, i.e. în semiplanul în care se află punctul (0; 0), -2 X – 2y+ 5≥ 0 și am fost întrebați unde -2 X – 2y+ 5 ≤ 0, prin urmare, într-un alt semiplan - în cel de deasupra dreptei.
Găsiți intersecția acestor două semiplane. Dreptele sunt paralele, deci planele nu se intersectează nicăieri, ceea ce înseamnă că sistemul acestor inegalități nu are soluții, este inconsecvent.

Exemplul 2. Găsiți grafic soluții ale sistemului de inegalități:

Figura 3
1. Notați ecuațiile corespunzătoare inegalităților și construiți drepte.
X + 2y– 2 = 0

X	2	0
y	0	1

y – X – 1 = 0

X	0	2
y	1	3

y + 2 = 0;
y = –2.
2. După ce am ales punctul (0; 0), determinăm semnele inegalităților în semiplanuri:
0 + 2 ∙ 0 – 2 ≤ 0, adică. X + 2y– 2 ≤ 0 în semiplanul de sub dreapta;
0 – 0 – 1 ≤ 0, adică y –X– 1 ≤ 0 în semiplanul de sub dreapta;
0 + 2 =2 ≥ 0, adică y+ 2 ≥ 0 în semiplanul de deasupra dreptei.
3. Intersecția acestor trei semiplane va fi o zonă care este un triunghi. Nu este dificil să găsiți vârfurile regiunii ca puncte de intersecție ale dreptelor corespunzătoare


În acest fel, DAR(–3; –2), LA(0; 1), DIN(6; –2).

Să luăm în considerare încă un exemplu, în care domeniul rezultat al soluției sistemului nu este limitat.