Logaritmus daného čísla sa nazýva exponent, na ktorý treba zvýšiť ďalšie číslo, tzv základ logaritmus na získanie tohto čísla. Napríklad základný 10 logaritmus čísla 100 je 2. Inými slovami, 10 musí byť odmocnené, aby sa získalo 100 (10 2 = 100). Ak n- dané číslo, b– základ a l– teda logaritmus b l = n. číslo n tiež nazývaný základný antilogaritmus bčísla l. Napríklad antilogaritmus 2 k základu 10 sa rovná 100. To možno zapísať vo forme protokolu vzťahov b n = l a antilog b l = n.

Základné vlastnosti logaritmov:

Akékoľvek iné kladné číslo ako jedna môže slúžiť ako základ pre logaritmy, ale bohužiaľ sa ukazuje, že ak b A n sú racionálne čísla, potom v zriedkavých prípadoch takéto racionálne číslo existuje l, Čo b l = n. Je však možné definovať iracionálne číslo l napríklad také, že 10 l= 2; toto je iracionálne číslo l možno aproximovať s akoukoľvek požadovanou presnosťou racionálnymi číslami. Ukazuje sa, že v uvedenom príklade l sa približne rovná 0,3010 a túto aproximáciu základného 10 logaritmu 2 možno nájsť v štvorciferných tabuľkách desiatkových logaritmov. Logaritmy so základňou 10 (alebo logaritmy so základňou 10) sa vo výpočtoch tak bežne používajú, že sa nazývajú obyčajný logaritmy a zapísané ako log2 = 0,3010 alebo log2 = 0,3010, pričom sa vynechá explicitná indikácia základu logaritmu. Logaritmy na základňu e, transcendentálne číslo približne rovné 2,71828 prirodzené logaritmy. Nachádzajú sa najmä v prácach o matematickej analýze a jej aplikáciách v rôznych vedách. Prirodzené logaritmy sa tiež píšu bez explicitného označenia základu, ale pomocou špeciálneho zápisu ln: napríklad ln2 = 0,6931, pretože e 0,6931 = 2.

Použitie tabuliek bežných logaritmov.

Pravidelný logaritmus čísla je exponent, na ktorý sa musí zvýšiť 10, aby sa získalo dané číslo. Keďže 10 0 = 1, 10 1 = 10 a 10 2 = 100, okamžite dostaneme, že log1 = 0, log10 = 1, log100 = 2 atď. pre rastúce celočíselné mocniny 10. Rovnako 10 –1 = 0,1, 10 –2 = 0,01 a teda log0,1 = –1, log0,01 = –2 atď. pre všetky záporné celočíselné mocniny 10. Zvyčajné logaritmy zostávajúcich čísel sú uzavreté medzi logaritmy najbližších celých čísel 10; log2 musí byť medzi 0 a 1, log20 musí byť medzi 1 a 2 a log0.2 musí byť medzi -1 a 0. Logaritmus teda pozostáva z dvoch častí, celého čísla a desatinného čísla, uzavretých medzi 0 a 1. celočíselná časť tzv charakteristický logaritmus a je určený samotným číslom, nazýva sa zlomková časť mantisa a nájdete ich v tabuľkách. Tiež log20 = log(2ґ10) = log2 + log10 = (log2) + 1. Logaritmus 2 je 0,3010, takže log20 = 0,3010 + 1 = 1,3010. Podobne log0,2 = log(2®10) = log2 – log10 = (log2) – 1 = 0,3010 – 1. Po odčítaní dostaneme log0,2 = – 0,6990. Je však vhodnejšie uviesť log0,2 ako 0,3010 – 1 alebo ako 9,3010 – 10; Dá sa sformulovať aj všeobecné pravidlo: všetky čísla získané z daného čísla vynásobením mocninou 10 majú zhodné mantisy rovné mantise daného čísla. Väčšina tabuliek zobrazuje mantisy čísel v rozsahu od 1 do 10, pretože mantisy všetkých ostatných čísel možno získať z čísel uvedených v tabuľke.

Väčšina tabuliek uvádza logaritmy so štyrmi alebo piatimi desatinnými miestami, hoci existujú aj sedemmiestne tabuľky a tabuľky s ešte väčším počtom desatinných miest. Najjednoduchší spôsob, ako sa naučiť používať takéto tabuľky, sú príklady. Aby sme našli log3.59, najprv si všimnime, že číslo 3,59 je medzi 10 0 a 10 1, takže jeho charakteristika je 0. Nájdeme číslo 35 (vľavo) v tabuľke a presunieme sa po riadku na stĺpec, ktorý má navrchu číslo 9; priesečník tohto stĺpca a riadku 35 je 5551, takže log3,59 = 0,5551. Ak chcete nájsť mantisu čísla so štyrmi platnými číslicami, musíte použiť interpoláciu. V niektorých tabuľkách je interpolácia uľahčená proporciami uvedenými v posledných deviatich stĺpcoch na pravej strane každej strany tabuliek. Teraz nájdime log736.4; číslo 736,4 leží medzi 10 2 a 10 3, preto charakteristika jeho logaritmu je 2. V tabuľke nájdeme riadok, naľavo od neho je 73 a stĺpec 6. Na priesečníku tohto riadka a tohto stĺpca je číslo 8669. Medzi lineárnymi časťami nájdeme stĺpec 4 Na priesečníku riadku 73 a stĺpca 4 je číslo 2. Pripočítaním 2 k 8669 dostaneme mantisu - rovná sa 8671. Log736,4 = 2,8671.

Prirodzené logaritmy.

Tabuľky a vlastnosti prirodzených logaritmov sú podobné tabuľkám a vlastnostiam bežných logaritmov. Hlavný rozdiel medzi oboma je v tom, že celočíselná časť prirodzeného logaritmu nie je podstatná pri určovaní polohy desatinnej čiarky, a preto rozdiel medzi mantisou a charakteristikou nehrá zvláštnu úlohu. Prirodzené logaritmy čísel 5,432; 54,32 a 543,2 sa rovnajú 1,6923; 3,9949 a 6,2975. Vzťah medzi týmito logaritmami bude zrejmý, ak vezmeme do úvahy rozdiely medzi nimi: log543,2 – log54,32 = 6,2975 – 3,9949 = 2,3026; posledné číslo nie je nič iné ako prirodzený logaritmus čísla 10 (napísané takto: ln10); log543,2 – log5,432 = 4,6052; posledné číslo je 2ln10. Ale 543,2 = 10ґ54,32 = 10 2ґ5,432. Teda prirodzeným logaritmom daného čísla a môžete nájsť prirodzené logaritmy čísel, ktoré sa rovnajú súčinom čísla a pre akýkoľvek stupeň nčísla 10 ak do ln a pridajte ln10 vynásobte n, t.j. ln( aґ10n) = log a + n ln10 = ln a + 2,3026n. Napríklad ln0,005432 = ln(5,432ґ10 –3) = ln5,432 – 3ln10 = 1,6923 – (3ґ2,3026) = – 5,2155. Preto tabuľky prirodzených logaritmov, podobne ako tabuľky bežných logaritmov, zvyčajne obsahujú iba logaritmy čísel od 1 do 10. V systéme prirodzených logaritmov možno hovoriť o antilogaritmoch, ale častejšie sa hovorí o exponenciálnej funkcii alebo exponente. Ak X= log r, To r = e x, A r nazývaný exponentom X(pre typografické pohodlie často píšu r= exp X). Exponent hrá úlohu antilogaritmu čísla X.

Pomocou tabuliek desiatkových a prirodzených logaritmov môžete vytvárať tabuľky logaritmov v akomkoľvek inom základe ako 10 a e. Ak log b a = X, To b x = a, a preto log c b x= log c a alebo X log c b= log c a, alebo X= log c a/log c b= log b a. Preto použite tento inverzný vzorec zo základnej logaritmickej tabuľky c môžete zostaviť tabuľky logaritmov v akejkoľvek inej základni b. Násobiteľ 1/log c b volal prechodový modul zo základne c do základne b. Nič nebráni napríklad použitiu inverzného vzorca alebo prechodu z jedného systému logaritmov do druhého, nájdeniu prirodzených logaritmov z tabuľky bežných logaritmov alebo vykonaniu spätného prechodu. Napríklad log105.432 = log e 5,432/log e 10 = 1,6923/2,3026 = 1,6923ґ0,4343 = 0,7350. Číslo 0,4343, ktorým sa musí prirodzený logaritmus daného čísla vynásobiť, aby sa získal obyčajný logaritmus, je modul prechodu do systému obyčajných logaritmov.

Špeciálne stoly.

Logaritmy boli pôvodne vynájdené tak, že pomocou ich vlastností log ab= log a+ denník b a log a/b= log a– log b, premeniť produkty na súčty a podiely na rozdiely. Inými slovami, ak log a a log b sú známe, potom pomocou sčítania a odčítania môžeme ľahko nájsť logaritmus súčinu a kvocientu. V astronómii sa však často uvádzajú hodnoty log a a log b treba nájsť log( a + b) alebo log( a – b). Samozrejme, najprv by sa dalo nájsť z tabuliek logaritmov a A b, potom vykonajte uvedené sčítanie alebo odčítanie a opäť s odkazom na tabuľky nájdite požadované logaritmy, ale takýto postup by si vyžadoval odkazovanie na tabuľky trikrát. Z. Leonelli v roku 1802 zverejnil tabuľky tzv. Gaussove logaritmy– logaritmy na sčítanie súčtov a rozdielov – čo umožnilo obmedziť sa na jeden prístup k tabuľkám.

V roku 1624 I. Kepler navrhol tabuľky proporcionálnych logaritmov, t.j. logaritmy čísel a/X, Kde a– nejaká kladná konštantná hodnota. Tieto tabuľky používajú predovšetkým astronómovia a navigátori.

Proporcionálne logaritmy pri a= 1 sa nazývajú kologaritmy a používajú sa pri výpočtoch, keď sa musíme zaoberať produktmi a podielmi. Kolaritmus čísla n rovná sa logaritmu recipročného čísla; tie. kolínska voda n= log1/ n= – log n. Ak log2 = 0,3010, potom colog2 = – 0,3010 = 0,6990 – 1. Výhodou použitia kologaritmov je, že pri výpočte hodnoty logaritmu výrazov ako napr. pq/r trojitý súčet kladných desatinných miest log p+ denník q+ kol r je ľahšie nájsť ako zmiešaný denník súčtu a rozdielu p+ denník q– log r.

Príbeh.

Princíp, ktorý je základom každého systému logaritmov, je známy už veľmi dlho a možno ho vysledovať až do starovekej babylonskej matematiky (približne 2000 pred Kristom). V tých dňoch sa na výpočet zloženého úroku používala interpolácia medzi tabuľkovými hodnotami kladných celočíselných mocnín celých čísel. Oveľa neskôr Archimedes (287 – 212 pred n. l.) použil mocniny 108 na nájdenie hornej hranice počtu zŕn piesku potrebných na úplné zaplnenie vtedy známeho vesmíru. Archimedes upozornil na vlastnosť exponentov, ktorá je základom účinnosti logaritmov: súčin mocnin zodpovedá súčtu exponentov. Na konci stredoveku a na začiatku novoveku sa matematici čoraz viac začali obracať na vzťah medzi geometrickými a aritmetickými postupmi. M. Stiefel vo svojej eseji Celočíselná aritmetika(1544) dal tabuľku kladných a záporných mocnín čísla 2:

Stiefel si všimol, že súčet dvoch čísel v prvom rade (riadok s exponentmi) sa rovná exponentu dvoch zodpovedajúcich súčinu dvoch zodpovedajúcich čísel v spodnom riadku (riadok s exponentmi). V súvislosti s touto tabuľkou Stiefel sformuloval štyri pravidlá ekvivalentné štyrom moderným pravidlám pre operácie s exponentmi alebo štyrom pravidlám pre operácie s logaritmami: súčet na hornom riadku zodpovedá súčinu na spodnom riadku; odčítanie na hornom riadku zodpovedá deleniu na spodnom riadku; násobenie na hornom riadku zodpovedá umocňovaniu na spodnom riadku; rozdelenie na hornom riadku zodpovedá zakoreneniu na spodnom riadku.

Pravidlá podobné Stiefelovým pravidlám viedli J. Napera k formálnemu zavedeniu prvého systému logaritmov vo svojej práci. Popis úžasnej tabuľky logaritmov, publikované v roku 1614. Ale Napierove myšlienky sa zaoberali problémom prepočtu produktov na sumy odvtedy, viac ako desať rokov pred vydaním svojej práce, dostal Napier správu z Dánska, že na observatóriu Tycha Braheho mali jeho asistenti metódu, vďaka ktorej je možné previesť produkty na sumy. Metóda diskutovaná v správe, ktorú Napier dostal, bola založená na použití trigonometrických vzorcov ako napr

preto Naperove tabuľky pozostávali hlavne z logaritmov goniometrických funkcií. Hoci pojem základ nebol explicitne zahrnutý v definícii navrhnutej Napierom, úlohu ekvivalentnú základni systému logaritmov v jeho systéme zohrávalo číslo (1 – 10 –7)ґ10 7, približne rovné 1/ e.

Nezávisle od Napera a takmer súčasne s ním vymyslel a vydal v roku 1620 J. Bürgi v Prahe typovo veľmi podobný systém logaritmov. Aritmetické a geometrické progresívne tabuľky. Boli to tabuľky antilogaritmov k základu (1 + 10 –4) ґ10 4, pomerne dobrá aproximácia počtu e.

V systéme Naper sa logaritmus čísla 107 považoval za nulu a keď sa čísla znižovali, logaritmy sa zvyšovali. Keď G. Briggs (1561–1631) navštívil Napier, obaja sa zhodli, že by bolo vhodnejšie použiť ako základ číslo 10 a logaritmus jednotky považovať za nulu. Potom, ako sa čísla zvýšili, ich logaritmy sa zvýšili. Získali sme tak moderný systém desiatkových logaritmov, ktorého tabuľku publikoval Briggs vo svojej práci Logaritmická aritmetika(1620). Logaritmy na základňu e, aj keď nie presne tie, ktoré predstavil Naper, sa často nazývajú Naperove. Pojmy "charakteristika" a "mantisa" navrhol Briggs.

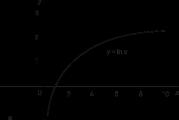
Prvé logaritmy z historických dôvodov používali aproximácie k číslam 1/ e A e. O niečo neskôr sa myšlienka prirodzených logaritmov začala spájať so štúdiom oblastí pod hyperbolou xy= 1 (obr. 1). V 17. storočí ukázalo sa, že oblasť ohraničená touto krivkou, os X a ordináty X= 1 a X = a(na obr. 1 je táto oblasť pokrytá výraznejšími a riedkymi bodkami) zvyšuje aritmetický postup, keď a rastie exponenciálne. Práve táto závislosť vzniká v pravidlách pre operácie s exponentmi a logaritmami. To viedlo k tomu, že sa Naperove logaritmy nazývali „hyperbolické logaritmy“.

Logaritmická funkcia.

Boli časy, keď sa logaritmy považovali len za výpočtový prostriedok, ale v 18. storočí sa najmä vďaka Eulerovmu dielu vytvoril koncept logaritmickej funkcie. Graf takejto funkcie r= log X, ktorého súradnice sa zvyšujú v aritmetickej progresii, zatiaľ čo úsečky sa zvyšujú v geometrickej progresii, je znázornené na obr. 2, A. Graf inverznej alebo exponenciálnej funkcie y = e x, ktorého súradnice sa zvyšujú v geometrickej progresii a ktorých úsečky sa zvyšujú v aritmetickej progresii, je znázornené na obr. 2, b. (Krivky r= log X A r = 10X tvarom podobný krivkám r= log X A r = e x.) Boli navrhnuté aj alternatívne definície logaritmickej funkcie, napr.

kpi; a podobne prirodzené logaritmy čísla -1 sú komplexné čísla tvaru (2 k + 1)pi, Kde k– celé číslo. Podobné tvrdenia platia pre všeobecné logaritmy alebo iné systémy logaritmov. Okrem toho, definícia logaritmov môže byť zovšeobecnená pomocou Eulerových identít tak, aby zahŕňala komplexné logaritmy komplexných čísel.

Alternatívnu definíciu logaritmickej funkcie poskytuje funkčná analýza. Ak f(X) – spojitá funkcia reálneho čísla X, ktorý má tieto tri vlastnosti: f (1) = 0, f (b) = 1, f (uv) = f (u) + f (v), To f(X) je definovaný ako logaritmus čísla X založené na b. Táto definícia má oproti definícii uvedenej na začiatku tohto článku množstvo výhod.

Aplikácie.

Logaritmy sa pôvodne používali výlučne na zjednodušenie výpočtov a táto aplikácia je stále jednou z ich najdôležitejších. Výpočet súčinov, kvocientov, mocnín a koreňov uľahčuje nielen široká dostupnosť publikovaných tabuliek logaritmov, ale aj použitie tzv. logaritmické pravítko - výpočtový nástroj, ktorého princíp fungovania je založený na vlastnostiach logaritmov. Pravítko je vybavené logaritmickými stupnicami, t.j. vzdialenosť od čísla 1 k ľubovoľnému číslu X zvolená tak, aby sa rovnala log X; Posunutím jednej stupnice voči druhej je možné vykresliť súčty alebo rozdiely logaritmov, čo umožňuje čítať priamo zo stupnice súčiny alebo podiely zodpovedajúcich čísel. Môžete tiež využiť výhody reprezentácie čísel v logaritmickej forme. logaritmický papier na vykresľovanie grafov (papier s logaritmickými stupnicami vytlačenými na oboch súradnicových osiach). Ak funkcia spĺňa mocninný zákon tvaru y = kxn, potom jeho logaritmický graf vyzerá ako priamka, pretože log r= log k + n log X– rovnica lineárna vzhľadom na log r a log X. Naopak, ak logaritmický graf nejakej funkčnej závislosti vyzerá ako priamka, potom je táto závislosť mocninová. Semi-log papier (kde os y má logaritmickú mierku a os x má jednotnú mierku) je užitočný, keď potrebujete identifikovať exponenciálne funkcie. Rovnice formulára y = kb rx sa vyskytujú vždy, keď sa množstvo, ako napríklad počet obyvateľov, množstvo rádioaktívneho materiálu alebo bankový zostatok, znižuje alebo zvyšuje rýchlosťou úmernou množstvu obyvateľstva, rádioaktívneho materiálu alebo peňazí, ktoré sú v súčasnosti k dispozícii. Ak sa takáto závislosť nakreslí na semilogaritmický papier, graf bude vyzerať ako priamka.

Logaritmická funkcia vzniká v spojení so širokou škálou prírodných foriem. Kvety v súkvetiach slnečnice sú usporiadané v logaritmických špirálach, lastúry mäkkýšov sú skrútené Nautilus, rohy horských oviec a zobáky papagájov. Všetky tieto prirodzené tvary môžu slúžiť ako príklady krivky známej ako logaritmická špirála, pretože v polárnom súradnicovom systéme je jej rovnica r = ae bq, alebo ln r= log a + bq. Takáto krivka je opísaná pohyblivým bodom, ktorého vzdialenosť od pólu sa geometrickým postupom zväčšuje a uhol opísaný jeho vektorom polomeru sa zväčšuje v aritmetickom postupe. Všadeprítomnosť takejto krivky, a teda aj logaritmickej funkcie, dobre ilustruje skutočnosť, že sa vyskytuje v takých vzdialených a úplne odlišných oblastiach, ako je obrys excentrickej vačky a trajektória nejakého hmyzu letiaceho smerom k svetlu.

Takže máme mocniny dvoch. Ak vezmete číslo zo spodného riadku, ľahko nájdete moc, na ktorú budete musieť zvýšiť dvojku, aby ste toto číslo získali. Napríklad, ak chcete získať 16, musíte zvýšiť dve na štvrtú mocninu. A aby ste získali 64, musíte zvýšiť dve na šiestu mocninu. To je možné vidieť z tabuľky.

A teraz vlastne definícia logaritmu:

Základ a logaritmus x je mocnina, na ktorú a musí byť zvýšená, aby dostal x.

Zápis: log a x = b, kde a je základ, x je argument, b je to, čomu sa v skutočnosti rovná logaritmus.

Napríklad 2 3 = 8 ⇒ log 2 8 = 3 (základný 2 logaritmus čísla 8 je tri, pretože 2 3 = 8). S rovnakým úspechom log 2 64 = 6, pretože 2 6 = 64.

Operácia nájdenia logaritmu čísla k danému základu sa nazýva logaritmizácia. Pridajme teda do tabuľky nový riadok:

2 1	2 2	2 3	2 4	2 5	2 6
2	4	8	16	32	64
log 2 2 = 1	log 2 4 = 2	log 2 8 = 3	log 2 16 = 4	log 2 32 = 5	log 2 64 = 6

Bohužiaľ, nie všetky logaritmy sa počítajú tak ľahko. Skúste napríklad nájsť log 2 5. Číslo 5 nie je v tabuľke, ale logika diktuje, že logaritmus bude ležať niekde na intervale. Pretože 22< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.

Takéto čísla sa nazývajú iracionálne: čísla za desatinnou čiarkou možno písať do nekonečna a nikdy sa neopakujú. Ak sa logaritmus ukáže ako iracionálny, je lepšie ho nechať tak: log 2 5, log 3 8, log 5 100.

Je dôležité pochopiť, že logaritmus je výraz s dvoma premennými (základ a argument). Mnoho ľudí si najskôr mätie, kde je základ a kde je argument. Aby ste predišli nepríjemným nedorozumeniam, pozrite sa na obrázok:

[Popis k obrázku]

Pred nami nie je nič iné ako definícia logaritmu. Pamätajte: logaritmus je sila, do ktorého musí byť základňa zabudovaná, aby sa získal argument. Je to podstavec, ktorý je mocne vyvýšený - na obrázku je zvýraznený červenou farbou. Ukazuje sa, že základňa je vždy na dne! Hneď na prvej hodine poviem svojim študentom toto úžasné pravidlo – a nevznikne zmätok.

Definíciu sme si vymysleli – ostáva už len naučiť sa počítať logaritmy, t.j. zbavte sa znaku „log“. Na začiatok si všimneme, že z definície vyplývajú dve dôležité skutočnosti:

1. Argument a základ musia byť vždy väčšie ako nula. Vyplýva to z definície stupňa racionálnym exponentom, na ktorý je redukovaná definícia logaritmu.
2. Základ musí byť odlišný od jedného, ​​pretože jeden v akomkoľvek stupni stále zostáva jedným. Z tohto dôvodu je otázka „na akú silu treba pozdvihnúť, aby sme dostali dve“ nezmyselná. Taký stupeň neexistuje!

Takéto obmedzenia sú tzv rozsah prijateľných hodnôt(ODZ). Ukazuje sa, že ODZ logaritmu vyzerá takto: log a x = b ⇒ x > 0, a > 0, a ≠ 1.

Všimnite si, že neexistujú žiadne obmedzenia na číslo b (hodnota logaritmu). Napríklad logaritmus môže byť záporný: log 2 0,5 = -1, pretože 0,5 = 2 -1.

Teraz však uvažujeme iba o číselných výrazoch, kde nie je potrebné poznať VA logaritmu. Všetky obmedzenia už autori úloh zohľadnili. Keď však do hry vstúpia logaritmické rovnice a nerovnosti, požiadavky DL sa stanú povinnými. Koniec koncov, základ a argument môže obsahovať veľmi silné konštrukcie, ktoré nemusia nevyhnutne zodpovedať vyššie uvedeným obmedzeniam.

Teraz sa pozrime na všeobecnú schému výpočtu logaritmov. Pozostáva z troch krokov:

1. Vyjadrite základ a a argument x ako mocninu s minimálnym možným základom väčším ako jedna. Po ceste je lepšie zbaviť sa desatinných miest;
2. Riešte rovnicu pre premennú b: x = a b ;
3. Výsledné číslo b bude odpoveďou.

To je všetko! Ak sa logaritmus ukáže ako iracionálny, bude to viditeľné už v prvom kroku. Požiadavka, aby bol základ väčší ako jedna, je veľmi dôležitá: znižuje sa tým pravdepodobnosť chyby a výrazne sa zjednodušujú výpočty. Je to rovnaké s desatinnými zlomkami: ak ich okamžite prevediete na obyčajné, bude oveľa menej chýb.

Pozrime sa, ako táto schéma funguje na konkrétnych príkladoch:

Úloha. Vypočítajte logaritmus: log 5 25

1. Predstavme si základ a argument ako mocninu päťky: 5 = 5 1 ; 25 = 52;
2. Poďme vytvoriť a vyriešiť rovnicu:
   log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2;
3. Dostali sme odpoveď: 2.

Úloha. Vypočítajte logaritmus:

[Popis k obrázku]

Úloha. Vypočítajte logaritmus: log 4 64

1. Predstavme si základ a argument ako mocninu dvoch: 4 = 2 2 ; 64 = 26;
2. Poďme vytvoriť a vyriešiť rovnicu:
   log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3;
3. Dostali sme odpoveď: 3.

Úloha. Vypočítajte logaritmus: log 16 1

1. Predstavme si základ a argument ako mocninu dvoch: 16 = 2 4 ; 1 = 20;
2. Poďme vytvoriť a vyriešiť rovnicu:
   log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0;
3. Dostali sme odpoveď: 0.

Úloha. Vypočítajte logaritmus: log 7 14

1. Predstavme si základ a argument ako mocninu siedmich: 7 = 7 1 ; 14 nemôže byť vyjadrené ako mocnina siedmich, pretože 7 1< 14 < 7 2 ;
2. Z predchádzajúceho odseku vyplýva, že logaritmus sa nepočíta;
3. Odpoveď je žiadna zmena: log 7 14.

Malá poznámka k poslednému príkladu. Ako si môžete byť istý, že číslo nie je presnou mocninou iného čísla? Je to veľmi jednoduché – stačí to započítať do hlavných faktorov. A ak takéto faktory nemožno zhromaždiť do mocnín s rovnakými exponentmi, potom pôvodné číslo nie je presná mocnina.

Úloha. Zistite, či sú čísla presné mocniny: 8; 48; 81; 35; 14.

8 = 2 · 2 · 2 = 2 3 - presný stupeň, pretože existuje len jeden multiplikátor;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 - nie je presná mocnina, pretože existujú dva faktory: 3 a 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 - presný stupeň;
35 = 7 · 5 - opäť nie presná mocnina;
14 = 7 · 2 - opäť nie presný stupeň;

Všimnite si tiež, že samotné prvočísla sú vždy presné mocniny samých seba.

Desatinný logaritmus

Niektoré logaritmy sú také bežné, že majú špeciálny názov a symbol.

Desatinný logaritmus x je logaritmus so základom 10, t.j. Mocnina, na ktorú treba zvýšiť číslo 10, aby sme získali číslo x. Označenie: lg x.

Napríklad log 10 = 1; lg100 = 2; lg 1000 = 3 - atď.

Keď sa odteraz v učebnici objaví fráza ako „Nájsť lg 0,01“, vedzte, že to nie je preklep. Toto je desiatkový logaritmus. Ak však tento zápis nepoznáte, vždy ho môžete prepísať:
log x = log 10 x

Všetko, čo platí pre bežné logaritmy, platí aj pre desiatkové logaritmy.

Prirodzený logaritmus

Existuje ďalší logaritmus, ktorý má svoje vlastné označenie. V niektorých ohľadoch je to ešte dôležitejšie ako desatinné číslo. Hovoríme o prirodzenom logaritme.

Prirodzený logaritmus x je logaritmus so základom e, t.j. mocnina, na ktorú treba zvýšiť číslo e, aby sme získali číslo x. Označenie: ln x .

Mnohí sa budú pýtať: aké je číslo e? Toto je iracionálne číslo, jeho presnú hodnotu nemožno nájsť a zapísať. Uvediem len prvé čísla:
e = 2,718281828459...

Nebudeme sa podrobne zaoberať tým, čo je toto číslo a prečo je potrebné. Pamätajte, že e je základom prirodzeného logaritmu:
ln x = log e x

Teda ln e = 1; lne2 = 2; ln e 16 = 16 - atď. Na druhej strane, ln 2 je iracionálne číslo. Vo všeobecnosti je prirodzený logaritmus akéhokoľvek racionálneho čísla iracionálny. Samozrejme okrem jedného: ln 1 = 0.

Pre prirodzené logaritmy platia všetky pravidlá, ktoré platia pre bežné logaritmy.

Zachovanie vášho súkromia je pre nás dôležité. Z tohto dôvodu sme vyvinuli Zásady ochrany osobných údajov, ktoré popisujú, ako používame a uchovávame vaše informácie. Prečítajte si naše postupy ochrany osobných údajov a ak máte nejaké otázky, dajte nám vedieť.

Zhromažďovanie a používanie osobných údajov

Osobné údaje sú údaje, ktoré možno použiť na identifikáciu alebo kontaktovanie konkrétnej osoby.

Keď nás budete kontaktovať, môžete byť kedykoľvek požiadaní o poskytnutie svojich osobných údajov.

Nižšie sú uvedené niektoré príklady typov osobných údajov, ktoré môžeme zhromažďovať, a ako môžeme tieto informácie použiť.

Aké osobné údaje zhromažďujeme:

• Keď odošlete žiadosť na stránke, môžeme zhromažďovať rôzne informácie vrátane vášho mena, telefónneho čísla, e-mailovej adresy atď.

Ako používame vaše osobné údaje:

• Osobné údaje, ktoré zhromažďujeme, nám umožňujú kontaktovať vás s jedinečnými ponukami, propagačnými akciami a inými udalosťami a pripravovanými udalosťami.
• Z času na čas môžeme použiť vaše osobné údaje na zasielanie dôležitých upozornení a komunikácie.
• Osobné údaje môžeme použiť aj na interné účely, ako je vykonávanie auditov, analýza údajov a rôzne výskumy, aby sme zlepšili služby, ktoré poskytujeme, a poskytli vám odporúčania týkajúce sa našich služieb.
• Ak sa zúčastníte žrebovania o ceny, súťaže alebo podobnej propagačnej akcie, môžeme použiť informácie, ktoré nám poskytnete, na správu takýchto programov.

Sprístupnenie informácií tretím stranám

Informácie, ktoré od vás dostaneme, nezverejňujeme tretím stranám.

Výnimky:

• V prípade potreby – v súlade so zákonom, súdnym konaním, v súdnom konaní a/alebo na základe verejných žiadostí alebo žiadostí vládnych orgánov na území Ruskej federácie – poskytnúť vaše osobné údaje. Môžeme tiež zverejniť informácie o vás, ak zistíme, že takéto zverejnenie je potrebné alebo vhodné na účely bezpečnosti, presadzovania práva alebo na iné účely verejného významu.
• V prípade reorganizácie, zlúčenia alebo predaja môžeme osobné údaje, ktoré zhromažďujeme, preniesť na príslušnú nástupnícku tretiu stranu.

Ochrana osobných údajov

Prijímame opatrenia – vrátane administratívnych, technických a fyzických – na ochranu vašich osobných údajov pred stratou, krádežou a zneužitím, ako aj neoprávneným prístupom, zverejnením, zmenou a zničením.

Rešpektovanie vášho súkromia na úrovni spoločnosti

Aby sme zaistili bezpečnosť vašich osobných údajov, informujeme našich zamestnancov o štandardoch ochrany osobných údajov a bezpečnosti a prísne presadzujeme postupy ochrany osobných údajov.

\(a^(b)=c\) \(\šípka doľava\) \(\log_(a)(c)=b\)

Poďme si to vysvetliť jednoduchšie. Napríklad \(\log_(2)(8)\) sa rovná mocnine, na ktorú musí byť umocnený \(2\), aby ste dostali \(8\). Z toho je jasné, že \(\log_(2)(8)=3\).

Príklady:		\(\log_(5)(25)=2\)		pretože \(5^(2)=25\)
		\(\log_(3)(81)=4\)		pretože \(3^(4)=81\)
		\(\log_(2)\)\(\frac(1)(32)\) \(=-5\)		pretože \(2^(-5)=\)\(\frac(1)(32)\)

Argument a základ logaritmu

Každý logaritmus má nasledujúcu „anatómiu“:

Argument logaritmu sa zvyčajne zapisuje na jeho úrovni a základňa sa píše dolným indexom bližšie k znamienku logaritmu. A tento záznam znie takto: „logaritmus dvadsaťpäť na základ päť“.

Ako vypočítať logaritmus?

Ak chcete vypočítať logaritmus, musíte odpovedať na otázku: na akú moc by sa mala zvýšiť základňa, aby ste dostali argument?

Napríklad, vypočítajte logaritmus: a) \(\log_(4)(16)\) b) \(\log_(3)\)\(\frac(1)(3)\) c) \(\log_(\ sqrt (5))(1)\) d) \(\log_(\sqrt(7))(\sqrt(7)\) e) \(\log_(3)(\sqrt(3))\)

a) Na akú mocninu treba zvýšiť \(4\), aby ste dostali \(16\)? Očividne ten druhý. Preto:

\(\log_(4)(16)=2\)

\(\log_(3)\)\(\frac(1)(3)\) \(=-1\)

c) Na akú mocninu sa musí zvýšiť \(\sqrt(5)\), aby sme dostali \(1\)? Aká sila robí ktorúkoľvek číslo jedna? Nula, samozrejme!

\(\log_(\sqrt(5))(1)=0\)

d) Na akú mocninu sa musí zvýšiť \(\sqrt(7)\), aby sa získal \(\sqrt(7)\)? Po prvé, akékoľvek číslo s prvou mocninou sa rovná samému sebe.

\(\log_(\sqrt(7))(\sqrt(7))=1\)

e) Na akú mocninu sa musí zvýšiť \(3\), aby sa získal \(\sqrt(3)\)? Z toho vieme, že ide o zlomkovú mocninu, čo znamená, že druhá odmocnina je mocninou \(\frac(1)(2)\) .

\(\log_(3)(\sqrt(3))=\)\(\frac(1)(2)\)

Príklad : Vypočítajte logaritmus \(\log_(4\sqrt(2))(8)\)

Riešenie :

\(\log_(4\sqrt(2))(8)=x\)		Musíme nájsť hodnotu logaritmu, označme ho ako x. Teraz použijeme definíciu logaritmu: \(\log_(a)(c)=b\) \(\Šípka doľava\) \(a^(b)=c\)
\((4\sqrt(2))^(x)=8\)		Čo spája \(4\sqrt(2)\) a \(8\)? Dve, ​​pretože obe čísla môžu byť reprezentované dvojkami: \(4=2^(2)\) \(\sqrt(2)=2^(\frac(1)(2))\) \(8=2^(3)\)
\(((2^(2)\cdot2^(\frac(1)(2))))^(x)=2^(3)\)		Vľavo používame vlastnosti stupňa: \(a^(m)\cdot a^(n)=a^(m+n)\) a \((a^(m))^(n)= a^(m\cdot n)\)
\(2^(\frac(5)(2)x)=2^(3)\)		Základy sú rovnaké, prechádzame k rovnosti ukazovateľov
\(\frac(5x)(2)\) \(=3\)		Vynásobte obe strany rovnice pomocou \(\frac(2)(5)\)
		Výsledný koreň je hodnota logaritmu

Odpoveď : \(\log_(4\sqrt(2))(8)=1,2\)

Prečo bol logaritmus vynájdený?

Aby sme to pochopili, vyriešme rovnicu: \(3^(x)=9\). Stačí priradiť \(x\), aby rovnica fungovala. Samozrejme, \(x=2\).

Teraz vyriešte rovnicu: \(3^(x)=8\).Čo sa rovná x? To je podstata.

Tí najmúdrejší povedia: "X je o niečo menej ako dva." Ako presne napísať toto číslo? Na zodpovedanie tejto otázky bol vynájdený logaritmus. Vďaka nemu tu môže byť odpoveď napísaná ako \(x=\log_(3)(8)\).

Chcem zdôrazniť, že \(\log_(3)(8)\), ako každý logaritmus je len číslo. Áno, vyzerá to nezvyčajne, ale je to krátke. Pretože ak by sme to chceli zapísať ako desatinné, vyzeralo by to takto: \(1.892789260714.....\)

Príklad : Vyriešte rovnicu \(4^(5x-4)=10\)

Riešenie :

\(4^(5x-4)=10\)		\(4^(5x-4)\) a \(10\) nemožno preniesť na rovnakú základňu. To znamená, že sa nezaobídete bez logaritmu. Použime definíciu logaritmu: \(a^(b)=c\) \(\šípka doľava\) \(\log_(a)(c)=b\)
\(\log_(4)(10)=5x-4\)		Otočme rovnicu tak, aby X bolo vľavo
\(5x-4=\log_(4)(10)\)		Pred nami. Presuňme \(4\) doprava. A nebojte sa logaritmu, zaobchádzajte s ním ako s obyčajným číslom.
\(5x=\log_(4)(10)+4\)		Rozdeľte rovnicu číslom 5
\(x=\)\(\frac(\log_(4)(10)+4)(5)\)		Toto je náš koreň. Áno, vyzerá to nezvyčajne, ale nevyberajú si odpoveď.

Odpoveď : \(\frac(\log_(4)(10)+4)(5)\)

Desatinné a prirodzené logaritmy

Ako je uvedené v definícii logaritmu, jeho základom môže byť akékoľvek kladné číslo okrem jedného \((a>0, a\neq1)\). A medzi všetkými možnými základmi sú dve, ktoré sa vyskytujú tak často, že na logaritmy s nimi bol vynájdený špeciálny krátky zápis:

Prirodzený logaritmus: logaritmus, ktorého základom je Eulerovo číslo \(e\) (rovná sa približne \(2,7182818…\)) a logaritmus sa zapíše ako \(\ln(a)\).

teda \(\ln(a)\) je to isté ako \(\log_(e)(a)\)

Desatinný logaritmus: Logaritmus, ktorého základ je 10, sa zapíše \(\lg(a)\).

teda \(\lg(a)\) je to isté ako \(\log_(10)(a)\), kde \(a\) je nejaké číslo.

Základná logaritmická identita

Logaritmy majú veľa vlastností. Jedna z nich sa nazýva „základná logaritmická identita“ a vyzerá takto:

\(a^(\log_(a)(c))=c\)

Táto vlastnosť vyplýva priamo z definície. Pozrime sa, ako presne tento vzorec vznikol.

Pripomeňme si krátky zápis definície logaritmu:

ak \(a^(b)=c\), potom \(\log_(a)(c)=b\)

To znamená, že \(b\) je to isté ako \(\log_(a)(c)\). Potom môžeme do vzorca \(a^(b)=c\) namiesto \(b\) napísať \(\log_(a)(c)\). Ukázalo sa, že \(a^(\log_(a)(c))=c\) - hlavná logaritmická identita.

Môžete nájsť ďalšie vlastnosti logaritmov. S ich pomocou môžete zjednodušiť a vypočítať hodnoty výrazov pomocou logaritmov, ktoré je ťažké vypočítať priamo.

Príklad : Nájdite hodnotu výrazu \(36^(\log_(6)(5))\)

Riešenie :

Odpoveď : \(25\)

Ako napísať číslo ako logaritmus?

Ako bolo uvedené vyššie, každý logaritmus je len číslo. Platí to aj naopak: ľubovoľné číslo možno zapísať ako logaritmus. Napríklad vieme, že \(\log_(2)(4)\) sa rovná dvom. Potom namiesto dvoch môžete napísať \(\log_(2)(4)\).

Ale \(\log_(3)(9)\) sa tiež rovná \(2\), čo znamená, že môžeme písať aj \(2=\log_(3)(9)\) . Podobne s \(\log_(5)(25)\) a s \(\log_(9)(81)\) atď. To znamená, že sa ukazuje

\(2=\log_(2)(4)=\log_(3)(9)=\log_(4)(16)=\log_(5)(25)=\log_(6)(36)=\ log_(7)(49)...\)

Ak teda potrebujeme, môžeme napísať dvojku ako logaritmus s ľubovoľným základom kdekoľvek (či už v rovnici, vo výraze alebo v nerovnosti) - jednoducho napíšeme základ na druhú ako argument.

Rovnako je to aj s trojkou – možno ju zapísať ako \(\log_(2)(8)\), alebo ako \(\log_(3)(27)\), alebo ako \(\log_(4)( 64) \)... Tu napíšeme základ v kocke ako argument:

\(3=\log_(2)(8)=\log_(3)(27)=\log_(4)(64)=\log_(5)(125)=\log_(6)(216)=\ log_(7)(343)...\)

A so štyrmi:

\(4=\log_(2)(16)=\log_(3)(81)=\log_(4)(256)=\log_(5)(625)=\log_(6)(1296)=\ log_(7)(2401)...\)

A s mínusom jedna:

\(-1=\) \(\log_(2)\)\(\frac(1)(2)\) \(=\) \(\log_(3)\)\(\frac(1)( 3)\) \(=\) \(\log_(4)\)\(\frac(1)(4)\) \(=\) \(\log_(5)\)\(\frac(1) )(5)\) \(=\) \(\log_(6)\)\(\frac(1)(6)\) \(=\) \(\log_(7)\)\(\frac (1) (7)\) \(...\)

A s jednou tretinou:

\(\frac(1)(3)\) \(=\log_(2)(\sqrt(2))=\log_(3)(\sqrt(3))=\log_(4)(\sqrt( 4))=\log_(5)(\sqrt(5))=\log_(6)(\sqrt(6))=\log_(7)(\sqrt(7))...\)

Akékoľvek číslo \(a\) môže byť vyjadrené ako logaritmus so základom \(b\): \(a=\log_(b)(b^(a))\)

Príklad : Nájdite význam výrazu \(\frac(\log_(2)(14))(1+\log_(2)(7))\)

Riešenie :

Odpoveď : \(1\)

Čo je to logaritmus?

Pozor!
Existujú ďalšie
materiály v osobitnom oddiele 555.
Pre tých, ktorí sú veľmi „nie veľmi...“
A pre tých, ktorí „veľmi...“)

Čo je to logaritmus? Ako vyriešiť logaritmy? Tieto otázky mätú mnohých absolventov. Tradične sa téma logaritmov považuje za zložitú, nepochopiteľnú a strašidelnú. Najmä rovnice s logaritmami.

Toto absolútne nie je pravda. Absolútne! neveríš mi? Dobre. Teraz, len za 10 - 20 minút:

1. Pochopíš čo je logaritmus.

2. Naučte sa riešiť celú triedu exponenciálnych rovníc. Aj keď ste o nich nič nepočuli.

3. Naučte sa počítať jednoduché logaritmy.

Navyše na to budete potrebovať iba poznať tabuľku násobenia a ako zvýšiť číslo na mocninu...

Mám pocit, že máš pochybnosti... Dobre, poznačte si čas! Choď!

Najprv si v hlave vyriešte túto rovnicu:

Ak sa vám táto stránka páči...

Mimochodom, mám pre vás niekoľko ďalších zaujímavých stránok.)

Môžete si precvičiť riešenie príkladov a zistiť svoju úroveň. Testovanie s okamžitým overením. Učme sa - so záujmom!)

Môžete sa zoznámiť s funkciami a derivátmi.