Logaritm al unui număr dat se numește exponentul la care trebuie ridicat un alt număr, numit bază logaritm pentru a obține acest număr. De exemplu, logaritmul de bază 10 al lui 100 este 2. Cu alte cuvinte, 10 trebuie să fie pătrat pentru a obține 100 (10 2 = 100). Dacă n- un număr dat, b– bază și l– logaritm, atunci b l = n. Număr n numit și antilogaritm de bază b numere l. De exemplu, antilogaritmul de la 2 la baza 10 este egal cu 100. Acesta poate fi scris sub forma jurnalului de relații b n = lși antilog b l = n.

Proprietățile de bază ale logaritmilor:

Orice număr pozitiv, altul decât unul, poate servi drept bază pentru logaritmi, dar, din păcate, se dovedește că dacă bȘi n sunt numere raționale, atunci în cazuri rare există un astfel de număr rațional l, Ce b l = n. Cu toate acestea, este posibil să se definească un număr irațional l, de exemplu, astfel încât 10 l= 2; acesta este un număr irațional l poate fi aproximat cu orice precizie cerută prin numere raționale. Se pare că în exemplul dat l este aproximativ egală cu 0,3010, iar această aproximare a logaritmului de bază 10 de 2 poate fi găsită în tabelele cu patru cifre ale logaritmilor zecimal. Logaritmii de bază 10 (sau logaritmii de bază 10) sunt atât de frecvent folosiți în calcule încât sunt numiți comun logaritmi și scris ca log2 = 0,3010 sau log2 = 0,3010, omițând indicarea explicită a bazei logaritmului. Logaritmi la bază e, un număr transcendental aproximativ egal cu 2,71828, se numesc natural logaritmi. Ele se găsesc în principal în lucrările de analiză matematică și aplicațiile acesteia la diferite științe. Logaritmii naturali se scriu, de asemenea, fără a indica în mod explicit baza, dar folosind notația specială ln: de exemplu, ln2 = 0,6931, deoarece e 0,6931 = 2.

Folosind tabele de logaritmi obișnuiți.

Logaritmul regulat al unui număr este un exponent la care trebuie crescut 10 pentru a obține un număr dat. Deoarece 10 0 = 1, 10 1 = 10 și 10 2 = 100, obținem imediat acel log1 = 0, log10 = 1, log100 = 2 etc. pentru mărirea puterilor întregi 10. La fel, 10 –1 = 0,1, 10 –2 = 0,01 și deci log0,1 = –1, log0,01 = –2 etc. pentru toate puterile întregi negative 10. Logaritmii obișnuiți ai numerelor rămase sunt încadrați între logaritmii celor mai apropiate puteri întregi de 10; log2 trebuie să fie între 0 și 1, log20 trebuie să fie între 1 și 2, iar log0.2 trebuie să fie între -1 și 0. Astfel, logaritmul este format din două părți, un întreg și o zecimală, cuprinse între 0 și 1. parte întreagă numită caracteristică logaritm și este determinată de numărul însuși, se numește partea fracțională mantisași pot fi găsite din tabele. De asemenea, log20 = log(2ґ10) = log2 + log10 = (log2) + 1. Logaritmul lui 2 este 0,3010, deci log20 = 0,3010 + 1 = 1,3010. În mod similar, log0.2 = log(2о10) = log2 – log10 = (log2) – 1 = 0.3010 – 1. După scădere, obținem log0.2 = – 0.6990. Cu toate acestea, este mai convenabil să reprezentați log0,2 ca 0,3010 – 1 sau ca 9,3010 – 10; Se poate formula și o regulă generală: toate numerele obținute dintr-un număr dat prin înmulțire cu o putere de 10 au mantise identice egale cu mantisa numărului dat. Majoritatea tabelelor arată mantisele numerelor din intervalul de la 1 la 10, deoarece mantisele tuturor celorlalte numere pot fi obținute din cele date în tabel.

Majoritatea tabelelor oferă logaritmi cu patru sau cinci zecimale, deși există tabele cu șapte cifre și tabele cu și mai multe zecimale. Cel mai simplu mod de a învăța cum să folosești astfel de tabele este cu exemple. Pentru a găsi log3.59, în primul rând, observăm că numărul 3.59 este între 10 0 și 10 1, deci caracteristica lui este 0. Găsim numărul 35 (în stânga) în tabel și ne deplasăm de-a lungul rândului la coloană care are numărul 9 în partea de sus ; intersecția acestei coloane cu rândul 35 este 5551, deci log3,59 = 0,5551. Pentru a găsi mantisa unui număr cu patru cifre semnificative, trebuie să utilizați interpolarea. În unele tabele, interpolarea este facilitată de proporțiile date în ultimele nouă coloane din partea dreaptă a fiecărei pagini a tabelelor. Să găsim acum log736.4; numărul 736,4 se află între 10 2 și 10 3, de aceea caracteristica logaritmului său este 2. În tabel găsim un rând în stânga căruia se află 73 și coloana 6. La intersecția acestui rând cu această coloană se află numărul 8669. Printre părțile liniare găsim coloana 4 La intersecția rândului 73 cu coloana 4 se află numărul 2. Adunând 2 la 8669, obținem mantisa - este egală cu 8671. Astfel, log736,4 = 2,8671.

Logaritmi naturali.

Tabelele și proprietățile logaritmilor naturali sunt similare cu tabelele și proprietățile logaritmilor obișnuiți. Principala diferență dintre ambele este că partea întreagă a logaritmului natural nu este semnificativă în determinarea poziției punctului zecimal și, prin urmare, diferența dintre mantise și caracteristică nu joacă un rol special. Logaritmi naturali ai numerelor 5,432; 54,32 și, respectiv, 543,2 sunt egale cu 1,6923; 3,9949 și 6,2975. Relația dintre acești logaritmi va deveni evidentă dacă luăm în considerare diferențele dintre ei: log543,2 – log54,32 = 6,2975 – 3,9949 = 2,3026; ultimul număr nu este altceva decât logaritmul natural al numărului 10 (scris astfel: ln10); log543,2 – log5,432 = 4,6052; ultimul număr este 2ln10. Dar 543,2 = 10ґ54,32 = 10 2ґ5,432. Astfel, prin logaritmul natural al unui număr dat A puteți găsi logaritmii naturali ai numerelor egale cu produsele numărului A pentru orice grad n numerele 10 dacă la ln A se adună ln10 înmulțit cu n, adică ln( Aґ10n) = jurnal A + n ln10 = ln A + 2,3026n. De exemplu, ln0,005432 = ln(5,432ґ10 –3) = ln5,432 – 3ln10 = 1,6923 – (3ґ2,3026) = – 5,2155. Prin urmare, tabelele de logaritmi naturali, ca și tabelele de logaritmi obișnuiți, conțin de obicei doar logaritmi de numere de la 1 la 10. În sistemul de logaritmi naturali, se poate vorbi despre antilogaritmi, dar mai des vorbesc despre o funcție exponențială sau un exponent. Dacă X= jurnal y, Acea y = e x, Și y numit exponent al X(pentru comoditate tipografică, ei scriu adesea y= exp X). Exponentul joacă rolul antilogaritmului numărului X.

Folosind tabele de logaritmi zecimali și naturali, puteți crea tabele de logaritmi în orice bază, alta decât 10 și e. Dacă log b a = X, Acea b x = A, și, prin urmare, log c b x= jurnal c a sau X Buturuga c b= jurnal c a, sau X= jurnal c a/Buturuga c b= jurnal b a. Prin urmare, folosind această formulă de inversare din tabelul de logaritm de bază c puteți construi tabele de logaritmi în orice altă bază b. Multiplicator 1/log c b numit modul de tranziție de la bază c până la bază b. Nimic nu împiedică, de exemplu, folosirea formulei de inversare sau trecerea de la un sistem de logaritmi la altul, găsirea de logaritmi naturali din tabelul logaritmilor obișnuiți sau efectuarea tranziției inverse. De exemplu, log105.432 = log e 5.432/log e 10 = 1,6923/2,3026 = 1,6923ґ0,4343 = 0,7350. Numărul 0,4343, cu care trebuie înmulțit logaritmul natural al unui număr dat pentru a obține un logaritm obișnuit, este modulul trecerii la sistemul de logaritmi obișnuiți.

Mese speciale.

Logaritmii au fost inventați inițial astfel încât, folosind proprietățile lor, jurnalul ab= jurnal A+ jurnal bși log A/b= jurnal A-Buturuga b, transformă produsele în sume și coeficientii în diferențe. Cu alte cuvinte, dacă log Ași log b sunt cunoscute, atunci folosind adunarea și scăderea putem găsi cu ușurință logaritmul produsului și coeficientul. În astronomie, totuși, adesea se dau valori de log Ași log b trebuie să găsesc jurnalul ( A + b) sau log( A – b). Desigur, s-ar putea găsi mai întâi din tabele de logaritmi AȘi b, apoi efectuați adunarea sau scăderea indicată și, referindu-vă din nou la tabele, găsiți logaritmii necesari, dar o astfel de procedură ar necesita referirea la tabele de trei ori. Z. Leonelli în 1802 a publicat tabele ale așa-numitelor. logaritmi gaussieni– logaritmi de adunare a sumelor și diferențelor – care au făcut posibil să se limiteze la un singur acces la tabele.

În 1624, I. Kepler a propus tabele de logaritmi proporționali, adică. logaritmi de numere A/X, Unde A– o valoare constantă pozitivă. Aceste tabele sunt folosite în principal de astronomi și navigatori.

Logaritmi proporționali la A= 1 sunt numite cologaritmiși sunt folosite în calcule atunci când se are de-a face cu produse și coeficienti. Coloritmul unui număr n egal cu logaritmul numărului reciproc; acestea. colg n= log1/ n= – jurnal n. Dacă log2 = 0,3010, atunci colog2 = – 0,3010 = 0,6990 – 1. Avantajul utilizării cologaritmilor este că atunci când se calculează valoarea logaritmului unor expresii precum pq/r suma triplă a zecimalelor pozitive log p+ jurnal q+colog r este mai ușor de găsit decât jurnalul de sumă și diferență mixtă p+ jurnal q-Buturuga r.

Poveste.

Principiul care stă la baza oricărui sistem de logaritmi este cunoscut de foarte mult timp și poate fi urmărit până la matematica antică babiloniană (circa 2000 î.Hr.). În acele zile, pentru a calcula dobânda compusă se folosea interpolarea între valorile din tabel ale puterilor întregi pozitive ale numerelor întregi. Mult mai târziu, Arhimede (287–212 î.Hr.) a folosit puterile lui 108 pentru a găsi o limită superioară a numărului de boabe de nisip necesare pentru a umple complet Universul cunoscut atunci. Arhimede a atras atenția asupra proprietății exponenților care stă la baza eficienței logaritmilor: produsul puterilor corespunde sumei exponenților. La sfârșitul Evului Mediu și începutul erei moderne, matematicienii au început să se orienteze din ce în ce mai mult către relația dintre progresiile geometrice și aritmetice. M. Stiefel în eseul său Aritmetica intregi(1544) a dat un tabel al puterilor pozitive și negative ale numărului 2:

Stiefel a observat că suma celor două numere din primul rând (rândul exponentului) este egală cu exponentul a doi corespunzător produsului dintre cele două numere corespunzătoare din rândul de jos (rândul exponentului). În legătură cu acest tabel, Stiefel a formulat patru reguli echivalente cu cele patru reguli moderne pentru operații pe exponenți sau cele patru reguli pentru operații pe logaritmi: suma de pe linia de sus corespunde produsului de pe linia de jos; scăderea pe linia de sus corespunde împărțirii pe linia de jos; înmulțirea pe linia de sus corespunde exponențiației pe linia de jos; diviziunea pe linia de sus corespunde cu înrădăcinarea pe linia de jos.

Aparent, reguli similare cu regulile lui Stiefel l-au determinat pe J. Naper să introducă în mod oficial primul sistem de logaritmi în lucrarea sa. Descrierea uimitoarei tabele de logaritmi, publicată în 1614. Însă gândurile lui Napier erau ocupate de problema conversiei produselor în sume de când, cu mai bine de zece ani înainte de publicarea lucrării sale, Napier a primit vești din Danemarca că la Observatorul Tycho Brahe asistenții săi aveau o metodă care făcea este posibilă transformarea produselor în sume. Metoda discutată în mesajul primit de Napier sa bazat pe utilizarea unor formule trigonometrice precum

prin urmare tabelele lui Naper constau în principal din logaritmi de funcții trigonometrice. Deși conceptul de bază nu a fost inclus în mod explicit în definiția propusă de Napier, rolul echivalent cu baza sistemului de logaritmi din sistemul său a fost jucat de numărul (1 – 10 –7)ґ10 7, aproximativ egal cu 1/ e.

Independent de Naper și aproape simultan cu el, un sistem de logaritmi, destul de asemănător ca tip, a fost inventat și publicat de J. Bürgi la Praga, publicat în 1620. Tabele de progresie aritmetică și geometrică. Acestea erau tabele de antilogaritmi la baza (1 + 10 –4) ґ10 4, o aproximare destul de bună a numărului e.

În sistemul Naper, logaritmul numărului 10 7 a fost considerat zero și, pe măsură ce numerele au scăzut, logaritmii au crescut. Când G. Briggs (1561–1631) a vizitat Napier, ambii au fost de acord că ar fi mai convenabil să se folosească numărul 10 ca bază și să considere logaritmul lui unu ca fiind zero. Apoi, pe măsură ce numerele creșteau, logaritmii lor ar crește. Astfel am obținut sistemul modern de logaritmi zecimal, al cărui tabel l-a publicat Briggs în lucrarea sa Aritmetică logaritmică(1620). Logaritmi la bază e, deși nu tocmai cele introduse de Naper, sunt adesea numite ale lui Naper. Termenii „caracteristic” și „mantișă” au fost propuși de Briggs.

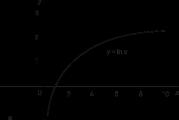
Primii logaritmi, din motive istorice, au folosit aproximări ale numerelor 1/ eȘi e. Ceva mai târziu, ideea logaritmilor naturali a început să fie asociată cu studiul zonelor sub o hiperbolă. X y= 1 (Fig. 1). În secolul al XVII-lea s-a arătat că aria delimitată de această curbă, axa X si ordonate X= 1 și X = A(în Fig. 1 această zonă este acoperită cu puncte mai îndrăznețe și rare) crește în progresia aritmetică atunci când A crește exponențial. Tocmai această dependență apare în regulile operațiilor cu exponenți și logaritmi. Acest lucru a dat naștere la numirea logaritmilor naperieni „logaritmi hiperbolici”.

Funcția logaritmică.

A existat o perioadă în care logaritmii erau considerați doar un mijloc de calcul, dar în secolul al XVIII-lea, în principal datorită lucrării lui Euler, s-a format conceptul de funcție logaritmică. Graficul unei astfel de funcții y= jurnal X, ale căror ordonate cresc în progresie aritmetică, în timp ce abscisele cresc în progresie geometrică, este prezentată în Fig. 2, A. Graficul unei funcții inverse sau exponențiale y = e x, ale căror ordonate cresc în progresie geometrică, iar abscisele cresc în progresie aritmetică, este prezentată, respectiv, în Fig. 2, b. (Curbe y= jurnal XȘi y = 10X asemănătoare ca formă cu curbele y= jurnal XȘi y = e x.) Au fost propuse și definiții alternative ale funcției logaritmice, de ex.

kpi; și, în mod similar, logaritmii naturali ai numărului -1 sunt numere complexe de forma (2 k + 1)pi, Unde k– un număr întreg. Afirmații similare sunt adevărate pentru logaritmii generali sau alte sisteme de logaritmi. În plus, definiția logaritmilor poate fi generalizată folosind identitățile lui Euler pentru a include logaritmi complexe de numere complexe.

O definiție alternativă a unei funcții logaritmice este oferită de analiza funcțională. Dacă f(X) – funcție continuă a unui număr real X, având următoarele trei proprietăți: f (1) = 0, f (b) = 1, f (uv) = f (u) + f (v), Acea f(X) este definit ca logaritmul numărului X bazat pe b. Această definiție are o serie de avantaje față de definiția dată la începutul acestui articol.

Aplicații.

Logaritmii au fost utilizați inițial doar pentru a simplifica calculele, iar această aplicație este încă una dintre cele mai importante. Calculul produselor, coeficientilor, puterilor și rădăcinilor este facilitat nu numai de disponibilitatea largă a tabelelor publicate de logaritmi, ci și de utilizarea așa-numitelor. regulă de calcul - un instrument de calcul al cărui principiu de funcționare se bazează pe proprietățile logaritmilor. Rigla este echipată cu scale logaritmice, adică. distanța de la numărul 1 la orice număr X ales să fie egal cu log X; Prin deplasarea unei scale în raport cu alta, este posibilă reprezentarea grafică a sumelor sau diferențelor de logaritmi, ceea ce face posibilă citirea direct de pe scară a produselor sau coeficientilor numerelor corespunzătoare. De asemenea, puteți profita de avantajele reprezentării numerelor în formă logaritmică. hârtie logaritmică pentru trasarea graficelor (hârtie cu scale logaritmice imprimate pe ambele axe de coordonate). Dacă o funcţie satisface o lege de putere de forma y = kxn, atunci graficul său logaritmic arată ca o linie dreaptă, deoarece Buturuga y= jurnal k + n Buturuga X– ecuația liniară în raport cu log yși log X. Dimpotrivă, dacă graficul logaritmic al unei dependențe funcționale arată ca o linie dreaptă, atunci această dependență este una de putere. Hârtia semi-log (unde axa y are o scară logaritmică și axa x are o scară uniformă) este utilă atunci când trebuie să identificați funcții exponențiale. Ecuații de formă y = kb rx apar ori de câte ori o cantitate, cum ar fi o populație, o cantitate de material radioactiv sau un sold bancar, scade sau crește într-o rată proporțională cu cantitatea de populație, material radioactiv sau bani disponibil în prezent. Dacă o astfel de dependență este reprezentată pe hârtie semilogaritmică, graficul va arăta ca o linie dreaptă.

Funcția logaritmică apare în legătură cu o mare varietate de forme naturale. Florile din inflorescențele de floarea soarelui sunt aranjate în spirale logaritmice, cochiliile de moluște sunt răsucite Nautilus, coarne de oaie de munte și ciocuri de papagal. Toate aceste forme naturale pot servi ca exemple de curbă cunoscută sub numele de spirală logaritmică deoarece, într-un sistem de coordonate polare, ecuația sa este r = ae bq, sau ln r= jurnal A + bq. O astfel de curbă este descrisă de un punct în mișcare, distanța de la polul căruia crește în progresie geometrică, iar unghiul descris de vectorul său rază crește în progresie aritmetică. Ubicuitatea unei astfel de curbe, și deci a funcției logaritmice, este bine ilustrată de faptul că apare în zone atât de îndepărtate și complet diferite precum conturul unei came excentrice și traiectoria unor insecte care zboară spre lumină.

Deci, avem puteri de doi. Dacă luați numărul din linia de jos, puteți găsi cu ușurință puterea la care va trebui să ridicați doi pentru a obține acest număr. De exemplu, pentru a obține 16, trebuie să ridicați doi la a patra putere. Și pentru a obține 64, trebuie să ridici doi la a șasea putere. Acest lucru se vede din tabel.

Și acum, de fapt, definiția logaritmului:

Baza a logaritmului lui x este puterea la care trebuie ridicat a pentru a obține x.

Notație: log a x = b, unde a este baza, x este argumentul, b este ceea ce este de fapt egal cu logaritmul.

De exemplu, 2 3 = 8 ⇒ log 2 8 = 3 (logaritmul de bază 2 al lui 8 este trei deoarece 2 3 = 8). Cu același succes, log 2 64 = 6, deoarece 2 6 = 64.

Operația de găsire a logaritmului unui număr la o bază dată se numește logaritmizare. Deci, să adăugăm o nouă linie la tabelul nostru:

2 1	2 2	2 3	2 4	2 5	2 6
2	4	8	16	32	64
log 2 2 = 1	log 2 4 = 2	log 2 8 = 3	log 2 16 = 4	log 2 32 = 5	log 2 64 = 6

Din păcate, nu toți logaritmii se calculează atât de ușor. De exemplu, încercați să găsiți log 2 5. Numărul 5 nu este în tabel, dar logica dictează că logaritmul va fi undeva pe interval. Pentru că 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.

Astfel de numere se numesc iraționale: numerele de după virgulă pot fi scrise la infinit și nu se repetă niciodată. Dacă logaritmul se dovedește a fi irațional, este mai bine să îl lăsați așa: log 2 5, log 3 8, log 5 100.

Este important să înțelegeți că un logaritm este o expresie cu două variabile (baza și argumentul). Mulți oameni confundă la început unde este baza și unde este argumentul. Pentru a evita neînțelegerile enervante, priviți imaginea:

[Letină pentru imagine]

În fața noastră nu este nimic altceva decât definiția unui logaritm. Tine minte: logaritmul este o putere, în care trebuie construită baza pentru a obține un argument. Este baza care este ridicată la o putere - este evidențiată cu roșu în imagine. Se dovedește că baza este întotdeauna în jos! Le spun studenților mei această regulă minunată chiar de la prima lecție - și nu apare nicio confuzie.

Ne-am dat seama de definiție - tot ce mai rămâne este să înveți cum să numărăm logaritmii, de exemplu. scapă de semnul „bușten”. Pentru început, observăm că din definiție rezultă două fapte importante:

1. Argumentul și baza trebuie să fie întotdeauna mai mari decât zero. Aceasta rezultă din definirea unui grad de către un exponent rațional, la care se reduce definiția unui logaritm.
2. Baza trebuie să fie diferită de unul, deoarece unul în orice grad rămâne unul. Din această cauză, întrebarea „la ce putere trebuie ridicat cineva pentru a obține doi” este lipsită de sens. Nu există o astfel de diplomă!

Se numesc astfel de restricții intervalul de valori acceptabile(ODZ). Rezultă că ODZ a logaritmului arată astfel: log a x = b ⇒ x > 0, a > 0, a ≠ 1.

Rețineți că nu există restricții privind numărul b (valoarea logaritmului). De exemplu, logaritmul poate fi foarte negativ: log 2 0.5 = −1, deoarece 0,5 = 2 −1.

Totuși, acum luăm în considerare doar expresii numerice, unde nu este necesar să cunoaștem VA logaritmului. Toate restricțiile au fost deja luate în considerare de către autorii problemelor. Dar atunci când ecuațiile și inegalitățile logaritmice intră în joc, cerințele DL vor deveni obligatorii. La urma urmei, baza și argumentul pot conține construcții foarte puternice care nu corespund neapărat restricțiilor de mai sus.

Acum să ne uităm la schema generală de calcul a logaritmilor. Acesta constă din trei etape:

1. Exprimați baza a și argumentul x ca o putere cu baza minimă posibilă mai mare decât unu. Pe parcurs, este mai bine să scapi de zecimale;
2. Rezolvați ecuația pentru variabila b: x = a b ;
3. Numărul rezultat b va fi răspunsul.

Asta e tot! Dacă logaritmul se dovedește a fi irațional, acesta va fi vizibil deja în primul pas. Cerința ca baza să fie mai mare decât unu este foarte importantă: aceasta reduce probabilitatea de eroare și simplifică foarte mult calculele. La fel este și cu fracțiile zecimale: dacă le convertiți imediat în unele obișnuite, vor exista mult mai puține erori.

Să vedem cum funcționează această schemă folosind exemple specifice:

Sarcină. Calculați logaritmul: log 5 25

1. Să ne imaginăm baza și argumentul ca o putere a lui cinci: 5 = 5 1 ; 25 = 5 2 ;
2. Să creăm și să rezolvăm ecuația:
   log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2;
3. Am primit răspunsul: 2.

Sarcină. Calculați logaritmul:

[Letină pentru imagine]

Sarcină. Calculați logaritmul: log 4 64

1. Să ne imaginăm baza și argumentul ca o putere a doi: 4 = 2 2 ; 64 = 2 6 ;
2. Să creăm și să rezolvăm ecuația:
   log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3;
3. Am primit răspunsul: 3.

Sarcină. Calculați logaritmul: log 16 1

1. Să ne imaginăm baza și argumentul ca o putere a doi: 16 = 2 4 ; 1 = 2 0 ;
2. Să creăm și să rezolvăm ecuația:
   log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0;
3. Am primit raspunsul: 0.

Sarcină. Calculați logaritmul: log 7 14

1. Să ne imaginăm baza și argumentul ca o putere a lui șapte: 7 = 7 1 ; 14 nu poate fi reprezentat ca o putere a șapte, deoarece 7 1< 14 < 7 2 ;
2. Din paragraful anterior rezultă că logaritmul nu contează;
3. Răspunsul este fără schimbare: log 7 14.

O mică notă despre ultimul exemplu. Cum poți fi sigur că un număr nu este o putere exactă a altui număr? Este foarte simplu - doar includeți-l în factori primi. Și dacă astfel de factori nu pot fi adunați în puteri cu aceiași exponenți, atunci numărul inițial nu este o putere exactă.

Sarcină. Aflați dacă numerele sunt puteri exacte: 8; 48; 81; 35; 14.

8 = 2 · 2 · 2 = 2 3 - grad exact, deoarece există un singur multiplicator;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 - nu este o putere exactă, întrucât există doi factori: 3 și 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 - grad exact;
35 = 7 · 5 - din nou nu este o putere exactă;
14 = 7 · 2 - din nou nu este un grad exact;

Rețineți, de asemenea, că numerele prime în sine sunt întotdeauna puteri exacte ale lor.

Logaritm zecimal

Unii logaritmi sunt atât de comune încât au un nume și un simbol special.

Logaritmul zecimal al lui x este logaritmul la baza 10, adică. Puterea la care trebuie ridicat numărul 10 pentru a obține numărul x. Denumire: lg x.

De exemplu, log 10 = 1; lg 100 = 2; lg 1000 = 3 - etc.

De acum înainte, când o expresie precum „Găsiți lg 0.01” apare într-un manual, să știți că aceasta nu este o greșeală de tipar. Acesta este un logaritm zecimal. Cu toate acestea, dacă nu sunteți familiarizat cu această notație, o puteți rescrie oricând:
log x = log 10 x

Tot ceea ce este adevărat pentru logaritmii obișnuiți este valabil și pentru logaritmii zecimali.

Logaritmul natural

Există un alt logaritm care are propria sa denumire. În unele privințe, este chiar mai important decât zecimală. Vorbim despre logaritmul natural.

Logaritmul natural al lui x este logaritmul la baza e, i.e. puterea la care trebuie ridicat numărul e pentru a obține numărul x. Denumire: ln x .

Mulți se vor întreba: care este numărul e? Acesta este un număr irațional; valoarea lui exactă nu poate fi găsită și notă. Voi da doar primele cifre:
e = 2,718281828459...

Nu vom intra în detaliu despre ce este acest număr și de ce este necesar. Nu uitați că e este baza logaritmului natural:
ln x = log e x

Astfel ln e = 1; ln e 2 = 2; ln e 16 = 16 - etc. Pe de altă parte, ln 2 este un număr irațional. În general, logaritmul natural al oricărui număr rațional este irațional. Cu excepția, desigur, a unuia: ln 1 = 0.

Pentru logaritmii naturali, toate regulile care sunt adevărate pentru logaritmii obișnuiți sunt valabile.

Menținerea confidențialității dvs. este importantă pentru noi. Din acest motiv, am dezvoltat o Politică de confidențialitate care descrie modul în care folosim și stocăm informațiile dumneavoastră. Vă rugăm să examinați practicile noastre de confidențialitate și să ne comunicați dacă aveți întrebări.

Colectarea și utilizarea informațiilor personale

Informațiile personale se referă la date care pot fi folosite pentru a identifica sau contacta o anumită persoană.

Vi se poate cere să furnizați informațiile dumneavoastră personale în orice moment când ne contactați.

Mai jos sunt câteva exemple de tipuri de informații personale pe care le putem colecta și cum putem folosi aceste informații.

Ce informații personale colectăm:

• Când trimiteți o cerere pe site, este posibil să colectăm diverse informații, inclusiv numele, numărul de telefon, adresa de e-mail etc.

Cum folosim informațiile dumneavoastră personale:

• Informațiile personale pe care le colectăm ne permit să vă contactăm cu oferte unice, promoții și alte evenimente și evenimente viitoare.
• Din când în când, putem folosi informațiile dumneavoastră personale pentru a trimite notificări și comunicări importante.
• De asemenea, putem folosi informații personale în scopuri interne, cum ar fi efectuarea de audituri, analize de date și diverse cercetări pentru a îmbunătăți serviciile pe care le oferim și pentru a vă oferi recomandări cu privire la serviciile noastre.
• Dacă participați la o tragere la sorți, la un concurs sau la o promoție similară, este posibil să folosim informațiile pe care le furnizați pentru a administra astfel de programe.

Dezvăluirea informațiilor către terți

Nu dezvăluim informațiile primite de la dumneavoastră către terți.

Excepții:

• Dacă este necesar - în conformitate cu legea, procedura judiciară, în cadrul procedurilor judiciare și/sau pe baza solicitărilor publice sau a solicitărilor din partea organismelor guvernamentale din Federația Rusă - să vă dezvăluiți informațiile personale. De asemenea, putem dezvălui informații despre dumneavoastră dacă stabilim că o astfel de dezvăluire este necesară sau adecvată pentru securitate, aplicarea legii sau alte scopuri de importanță publică.
• În cazul unei reorganizări, fuziuni sau vânzări, este posibil să transferăm informațiile personale pe care le colectăm terței părți succesoare aplicabile.

Protecția informațiilor personale

Luăm măsuri de precauție - inclusiv administrative, tehnice și fizice - pentru a vă proteja informațiile personale împotriva pierderii, furtului și utilizării greșite, precum și împotriva accesului, dezvăluirii, modificării și distrugerii neautorizate.

Respectarea vieții private la nivelul companiei

Pentru a ne asigura că informațiile dumneavoastră personale sunt în siguranță, comunicăm angajaților noștri standarde de confidențialitate și securitate și aplicăm strict practicile de confidențialitate.

\(a^(b)=c\) \(\Leftrightarrow\) \(\log_(a)(c)=b\)

Să explicăm mai simplu. De exemplu, \(\log_(2)(8)\) este egal cu puterea la care trebuie ridicat \(2\) pentru a obține \(8\). Din aceasta rezultă clar că \(\log_(2)(8)=3\).

Exemple:		\(\log_(5)(25)=2\)		deoarece \(5^(2)=25\)
		\(\log_(3)(81)=4\)		deoarece \(3^(4)=81\)
		\(\log_(2)\)\(\frac(1)(32)\) \(=-5\)		deoarece \(2^(-5)=\)\(\frac(1)(32)\)

Argumentul și baza logaritmului

Orice logaritm are următoarea „anatomie”:

Argumentul unui logaritm este de obicei scris la nivelul său, iar baza este scrisă în indice mai aproape de semnul logaritmului. Și această intrare se citește astfel: „logaritm de douăzeci și cinci la baza cinci”.

Cum se calculează logaritmul?

Pentru a calcula logaritmul, trebuie să răspundeți la întrebarea: la ce putere ar trebui ridicată baza pentru a obține argumentul?

De exemplu, calculați logaritmul: a) \(\log_(4)(16)\) b) \(\log_(3)\)\(\frac(1)(3)\) c) \(\log_(\ sqrt (5))(1)\) d) \(\log_(\sqrt(7))(\sqrt(7))\) e) \(\log_(3)(\sqrt(3))\)

a) La ce putere trebuie ridicat \(4\) pentru a obține \(16\)? Evident, al doilea. De aceea:

\(\log_(4)(16)=2\)

\(\log_(3)\)\(\frac(1)(3)\) \(=-1\)

c) La ce putere trebuie ridicată \(\sqrt(5)\) pentru a obține \(1\)? Ce putere face pe orice număr unu? Zero, desigur!

\(\log_(\sqrt(5))(1)=0\)

d) La ce putere trebuie ridicată \(\sqrt(7)\) pentru a obține \(\sqrt(7)\)? În primul rând, orice număr la prima putere este egal cu el însuși.

\(\log_(\sqrt(7))(\sqrt(7))=1\)

e) La ce putere trebuie ridicată \(3\) pentru a obține \(\sqrt(3)\)? Din știm că este o putere fracțională, ceea ce înseamnă că rădăcina pătrată este puterea lui \(\frac(1)(2)\) .

\(\log_(3)(\sqrt(3))=\)\(\frac(1)(2)\)

Exemplu : Calculați logaritmul \(\log_(4\sqrt(2))(8)\)

Soluţie :

\(\log_(4\sqrt(2))(8)=x\)		Trebuie să găsim valoarea logaritmului, să o notăm cu x. Acum să folosim definiția unui logaritm: \(\log_(a)(c)=b\) \(\Leftrightarrow\) \(a^(b)=c\)
\((4\sqrt(2))^(x)=8\)		Ce leagă \(4\sqrt(2)\) și \(8\)? Doi, deoarece ambele numere pot fi reprezentate prin doi: \(4=2^(2)\) \(\sqrt(2)=2^(\frac(1)(2))\) \(8=2^(3)\)
\(((2^(2)\cdot2^(\frac(1)(2))))^(x)=2^(3)\)		În stânga folosim proprietățile gradului: \(a^(m)\cdot a^(n)=a^(m+n)\) și \((a^(m))^(n)= a^(m\cdot n)\)
\(2^(\frac(5)(2)x)=2^(3)\)		Bazele sunt egale, trecem la egalitatea indicatorilor
\(\frac(5x)(2)\) \(=3\)		Înmulțiți ambele părți ale ecuației cu \(\frac(2)(5)\)
		Rădăcina rezultată este valoarea logaritmului

Răspuns : \(\log_(4\sqrt(2))(8)=1,2\)

De ce a fost inventat logaritmul?

Pentru a înțelege acest lucru, să rezolvăm ecuația: \(3^(x)=9\). Doar potriviți \(x\) pentru ca ecuația să funcționeze. Desigur, \(x=2\).

Acum rezolvați ecuația: \(3^(x)=8\). Cu ce ​​este x egal? Acesta este ideea.

Cei mai deștepți vor spune: „X este puțin mai puțin de doi”. Cum să scriu mai exact acest număr? Pentru a răspunde la această întrebare, a fost inventat logaritmul. Datorită lui, răspunsul de aici poate fi scris ca \(x=\log_(3)(8)\).

Vreau să subliniez că \(\log_(3)(8)\), ca orice logaritm este doar un număr. Da, pare neobișnuit, dar este scurt. Pentru că dacă am vrea să-l scriem ca zecimală, ar arăta astfel: \(1.892789260714.....\)

Exemplu : Rezolvați ecuația \(4^(5x-4)=10\)

Soluţie :

\(4^(5x-4)=10\)		\(4^(5x-4)\) și \(10\) nu pot fi aduse la aceeași bază. Aceasta înseamnă că nu te poți descurca fără un logaritm. Să folosim definiția logaritmului: \(a^(b)=c\) \(\Leftrightarrow\) \(\log_(a)(c)=b\)
\(\log_(4)(10)=5x-4\)		Să răsturnăm ecuația astfel încât X să fie în stânga
\(5x-4=\log_(4)(10)\)		Înaintea noastră. Să ne deplasăm \(4\) la dreapta. Și nu vă fie teamă de logaritm, tratați-l ca pe un număr obișnuit.
\(5x=\log_(4)(10)+4\)		Împărțiți ecuația la 5
\(x=\)\(\frac(\log_(4)(10)+4)(5)\)		Aceasta este rădăcina noastră. Da, pare neobișnuit, dar ei nu aleg răspunsul.

Răspuns : \(\frac(\log_(4)(10)+4)(5)\)

Logaritmi zecimali și naturali

După cum se precizează în definiția unui logaritm, baza acestuia poate fi orice număr pozitiv, cu excepția unuia \((a>0, a\neq1)\). Și dintre toate bazele posibile, există două care apar atât de des încât a fost inventată o notație scurtă specială pentru logaritmi cu ele:

Logaritm natural: un logaritm a cărui bază este numărul lui Euler \(e\) (egal cu aproximativ \(2,7182818…\)), iar logaritmul se scrie ca \(\ln(a)\).

Acesta este, \(\ln(a)\) este același cu \(\log_(e)(a)\)

Logaritm zecimal: Un logaritm a cărui bază este 10 se scrie \(\lg(a)\).

Acesta este, \(\lg(a)\) este același cu \(\log_(10)(a)\), unde \(a\) este un număr.

Identitatea logaritmică de bază

Logaritmii au multe proprietăți. Una dintre ele se numește „Identitatea logaritmică de bază” și arată astfel:

\(a^(\log_(a)(c))=c\)

Această proprietate decurge direct din definiție. Să vedem exact cum a apărut această formulă.

Să ne amintim o scurtă notație a definiției logaritmului:

dacă \(a^(b)=c\), atunci \(\log_(a)(c)=b\)

Adică, \(b\) este același cu \(\log_(a)(c)\). Apoi putem scrie \(\log_(a)(c)\) în loc de \(b\) în formula \(a^(b)=c\). S-a dovedit \(a^(\log_(a)(c))=c\) - principala identitate logaritmică.

Puteți găsi alte proprietăți ale logaritmilor. Cu ajutorul lor, puteți simplifica și calcula valorile expresiilor cu logaritmi, care sunt dificil de calculat direct.

Exemplu : Găsiți valoarea expresiei \(36^(\log_(6)(5))\)

Soluţie :

Răspuns : \(25\)

Cum se scrie un număr ca logaritm?

După cum am menționat mai sus, orice logaritm este doar un număr. Este adevărat și invers: orice număr poate fi scris ca logaritm. De exemplu, știm că \(\log_(2)(4)\) este egal cu doi. Apoi, în loc de două, puteți scrie \(\log_(2)(4)\).

Dar \(\log_(3)(9)\) este, de asemenea, egal cu \(2\), ceea ce înseamnă că putem scrie și \(2=\log_(3)(9)\) . La fel și cu \(\log_(5)(25)\), și cu \(\log_(9)(81)\), etc. Adică se dovedește

\(2=\log_(2)(4)=\log_(3)(9)=\log_(4)(16)=\log_(5)(25)=\log_(6)(36)=\ log_(7)(49)...\)

Astfel, dacă avem nevoie, putem scrie doi ca logaritm cu orice bază oriunde (fie ea într-o ecuație, într-o expresie sau într-o inegalitate) - pur și simplu scriem baza la pătrat ca argument.

Este la fel și cu triplul – poate fi scris ca \(\log_(2)(8)\), sau ca \(\log_(3)(27)\), sau ca \(\log_(4)( 64) \)... Aici scriem baza în cub ca argument:

\(3=\log_(2)(8)=\log_(3)(27)=\log_(4)(64)=\log_(5)(125)=\log_(6)(216)=\ log_(7)(343)...\)

Și cu patru:

\(4=\log_(2)(16)=\log_(3)(81)=\log_(4)(256)=\log_(5)(625)=\log_(6)(1296)=\ log_(7)(2401)...\)

Și cu minus unu:

\(-1=\) \(\log_(2)\)\(\frac(1)(2)\) \(=\) \(\log_(3)\)\(\frac(1)( 3)\) \(=\) \(\log_(4)\)\(\frac(1)(4)\) \(=\) \(\log_(5)\)\(\frac(1) )(5)\) \(=\) \(\log_(6)\)\(\frac(1)(6)\) \(=\) \(\log_(7)\)\(\frac (1)(7)\) \(...\)

Și cu o treime:

\(\frac(1)(3)\) \(=\log_(2)(\sqrt(2))=\log_(3)(\sqrt(3))=\log_(4)(\sqrt( 4))=\log_(5)(\sqrt(5))=\log_(6)(\sqrt(6))=\log_(7)(\sqrt(7))...\)

Orice număr \(a\) poate fi reprezentat ca un logaritm cu baza \(b\): \(a=\log_(b)(b^(a))\)

Exemplu : Găsiți sensul expresiei \(\frac(\log_(2)(14))(1+\log_(2)(7))\)

Soluţie :

Răspuns : \(1\)

Ce este un logaritm?

Atenţie!
Există suplimentare
materiale din secțiunea specială 555.
Pentru cei care sunt foarte „nu foarte...”
Și pentru cei care „foarte mult...”)

Ce este un logaritm? Cum se rezolvă logaritmii? Aceste întrebări îi încurcă pe mulți absolvenți. În mod tradițional, subiectul logaritmilor este considerat complex, de neînțeles și înfricoșător. În special ecuații cu logaritmi.

Acest lucru nu este absolut adevărat. Absolut! Nu mă crezi? Amenda. Acum, în doar 10 - 20 de minute:

1. Vei intelege ce este un logaritm.

2. Învață să rezolvi o întreagă clasă de ecuații exponențiale. Chiar dacă nu ai auzit nimic despre ei.

3. Învață să calculezi logaritmi simpli.

Mai mult, pentru asta va trebui doar să cunoști tabla înmulțirii și cum să ridici un număr la o putere...

Simt că ai îndoieli... Ei bine, bine, marchează timpul! Merge!

Mai întâi, rezolvă această ecuație în capul tău:

Daca va place acest site...

Apropo, mai am câteva site-uri interesante pentru tine.)

Puteți exersa rezolvarea exemplelor și puteți afla nivelul dvs. Testare cu verificare instantanee. Să învățăm - cu interes!)

Vă puteți familiariza cu funcțiile și derivatele.