Logaritmus egy adott szám kitevőjének nevezzük, amelyre egy másik számot kell emelni, hívni alapján logaritmussal kapjuk meg ezt a számot. Például a 100-as 10-es bázis logaritmusa 2. Más szóval, 10-et négyzetre kell emelni, hogy 100-at kapjunk (10 2 = 100). Ha n- adott szám, b– alap és l– akkor logaritmus b l = n. Szám n bázisantilogaritmusnak is nevezik b számok l. Például a 2 és a 10 közötti antilogaritmus egyenlő 100-zal. Ez felírható a relációs napló formájában b n = lés antilog b l = n.

A logaritmus alapvető tulajdonságai:

Az egytől eltérő bármely pozitív szám szolgálhat logaritmus alapjául, de sajnos kiderül, hogy ha bÉs n racionális számok, akkor ritka esetekben van ilyen racionális szám l, Mit b l = n. Azonban lehetséges irracionális szám definiálása l például úgy, hogy a 10 l= 2; ez egy irracionális szám l racionális számokkal tetszőleges pontossággal közelíthető. Az adott példából kiderül l megközelítőleg egyenlő 0,3010-nel, és a 2-es 10-es alap logaritmusának ez a közelítése megtalálható a decimális logaritmusok négyjegyű táblázataiban. A 10-es alapú logaritmusokat (vagy 10-es logaritmusokat) olyan gyakran használják a számításokban, hogy ún. rendes logaritmusokat, és a log2 = 0,3010 vagy log2 = 0,3010 alakban írják le, figyelmen kívül hagyva a logaritmus alapjának kifejezett jelzését. Logaritmus az alaphoz e, egy transzcendentális szám, amely megközelítőleg egyenlő 2,71828-cal természetes logaritmusok. Főleg a matematikai elemzéssel és annak különféle tudományokban való alkalmazásaival foglalkozó munkákban találhatók meg. A természetes logaritmusokat is úgy írják le, hogy a bázist nem kifejezetten megadják, hanem az ln speciális jelöléssel: például ln2 = 0,6931, mert e 0,6931 = 2.

Közönséges logaritmus táblázatok használata.

Egy szám szabályos logaritmusa egy kitevő, amelyre 10-et kell emelni, hogy adott számot kapjunk. Mivel 10 0 = 1, 10 1 = 10 és 10 2 = 100, azonnal azt kapjuk, hogy log1 = 0, log10 = 1, log100 = 2 stb. egész hatványok növelésére 10. Hasonlóképpen 10 –1 = 0,1, 10 –2 = 0,01 és ezért log0,1 = –1, log0,01 = –2 stb. minden negatív egész hatványra 10. A fennmaradó számok szokásos logaritmusai a 10 legközelebbi egész hatványainak logaritmusai közé vannak zárva; A log2-nek 0 és 1 között kell lennie, a log20-nak 1 és 2 között, a log0.2-nek pedig -1 és 0 között kell lennie. Így a logaritmus két részből áll, egy egész számból és egy decimális számból, amelyek 0 és 1 közé vannak zárva. nevezett egész rész jellegzetes logaritmus és maga a szám határozza meg, a tört részt hívják mantissza táblázatokból pedig megtalálhatók. Továbbá log20 = log(2ґ10) = log2 + log10 = (log2) + 1. A 2 logaritmusa 0,3010, tehát log20 = 0,3010 + 1 = 1,3010. Hasonlóképpen log0.2 = log(2о10) = log2 – log10 = (log2) – 1 = 0.3010 – 1. Kivonás után log0.2 = – 0.6990-et kapunk. Kényelmesebb azonban a log0.2-t 0,3010 – 1-ként vagy 9,3010 – 10-ként ábrázolni; Megfogalmazható egy általános szabály is: egy adott számból 10 hatványával kapott összes szám mantisszája megegyezik az adott szám mantisszával. A legtöbb táblázat a számok mantisszáját 1-től 10-ig terjedő tartományban mutatja, mivel az összes többi szám mantisszáját a táblázatban megadottakból kaphatjuk meg.

A legtöbb táblázat négy-öt tizedesjegyű logaritmusokat ad, bár vannak hétjegyű és még több tizedesjegyű táblázatok is. Az ilyen táblázatok használatát a legegyszerűbben példákon keresztül tanulhatja meg. A log3.59 megtalálásához először is meg kell jegyezni, hogy a 3.59 szám 10 0 és 10 1 között van, tehát karakterisztikája 0. Megkeressük a táblázatban a 35-ös számot (bal oldalon), és a sorban haladva a oszlop, amelynek tetején a 9-es szám van; ennek az oszlopnak és a 35. sor metszéspontja 5551, tehát log3,59 = 0,5551. A négy jelentős számjegyből álló szám mantisszának meghatározásához interpolációt kell alkalmazni. Egyes táblázatokban az interpolációt megkönnyítik a táblázatok minden oldalának jobb oldalán az utolsó kilenc oszlopban megadott arányok. Keressük most a log736.4-et; a 736,4 szám 10 2 és 10 3 között van, ezért logaritmusának karakterisztikája 2. A táblázatban találunk egy sort, amelynek bal oldalán 73 és 6 oszlop található. Ennek a sornak és ennek az oszlopnak a metszéspontjában van A lineáris részek között találjuk a 4. oszlopot A 73. sor és a 4. oszlop metszéspontjában a 2. szám található. Ha 2-t adunk 8669-hez, megkapjuk a mantisszát - ez egyenlő 8671-gyel. Így log736.4 = 2,8671.

Természetes logaritmusok.

A természetes logaritmusok táblázatai és tulajdonságai hasonlóak a közönséges logaritmusok táblázataihoz és tulajdonságaihoz. A fő különbség a kettő között az, hogy a természetes logaritmus egész része nem jelentős a tizedesvessző helyzetének meghatározásában, ezért a mantissza és a karakterisztika különbsége nem játszik különösebb szerepet. Számok természetes logaritmusa 5,432; 54,32 és 543,2 egyenlő 1,6923-mal; 3,9949 és 6,2975. A logaritmusok közötti kapcsolat nyilvánvalóvá válik, ha figyelembe vesszük a köztük lévő különbségeket: log543,2 – log54,32 = 6,2975 – 3,9949 = 2,3026; az utolsó szám nem más, mint a 10-es szám természetes logaritmusa (így írva: ln10); log543,2 – log5,432 = 4,6052; az utolsó szám 2ln10. De 543,2 = 10ґ54,32 = 10 2ґ5,432. Így egy adott szám természetes logaritmusával a megtalálhatja a számok természetes logaritmusait, amelyek megegyeznek a szám szorzatával a bármilyen fokozatra n számok 10 if to ln a add hozzá ln10 szorozva n, azaz ln( aґ10n) = log a + n ln10 = ln a + 2,3026n. Például ln0,005432 = ln(5,432ґ10 –3) = ln5,432 – 3ln10 = 1,6923 – (3ґ2,3026) = – 5,2155. Ezért a természetes logaritmusok táblázatai a közönséges logaritmusokhoz hasonlóan általában csak 1-től 10-ig terjedő számok logaritmusait tartalmazzák. A természetes logaritmusok rendszerében beszélhetünk antilogaritmusokról, de gyakrabban beszélnek exponenciális függvényről vagy kitevőről. Ha x= log y, Azt y = e x, És y kitevőjének nevezzük x(a tipográfiai kényelem érdekében gyakran írnak y= exp x). A kitevő a szám antilogaritmusának szerepét tölti be x.

A tizedes és természetes logaritmustáblázatok használatával létrehozhat logaritmustáblázatokat a 10-től és a e. Ha log b a = x, Azt b x = a, és ezért log c b x=napló c a vagy x log c b=napló c a, vagy x=napló c a/log c b=napló b a. Ezért használja ezt az inverziós képletet az alap logaritmus táblázatból c logaritmustáblázatokat bármilyen más alapra építhet b. Szorzó 1/log c b hívott átmeneti modul az alaptól c a bázisra b. Semmi sem akadályozza meg például az inverziós képlet használatát vagy az egyik logaritmusrendszerből a másikba való átmenetet, a természetes logaritmusok megtalálását a közönséges logaritmusok táblázatából vagy a fordított átmenetet. Például log105.432 = log e 5,432/log e 10 = 1,6923/2,3026 = 1,6923ґ0,4343 = 0,7350. A 0,4343 szám, amellyel egy adott szám természetes logaritmusát meg kell szorozni, hogy közönséges logaritmust kapjunk, a közönséges logaritmusok rendszerére való átmenet modulusa.

Különleges asztalok.

A logaritmusokat eredetileg úgy találták ki, hogy tulajdonságaik segítségével log ab=napló a+ napló bés naplózza a/b=napló a–napló b, a termékeket összegekké, a hányadosokat pedig különbségekké alakítja. Más szóval, ha log aés naplózza b ismertek, akkor összeadás és kivonás segítségével könnyen megtalálhatjuk a szorzat logaritmusát és a hányadost. A csillagászatban azonban gyakran a log értékeket adják meg aés naplózza b meg kell találni a naplót ( a + b) vagy log( a – b). Természetesen először a logaritmustáblázatokból lehetett megtalálni aÉs b, majd hajtsa végre a jelzett összeadást vagy kivonást, és ismét a táblázatokra hivatkozva keresse meg a szükséges logaritmusokat, de egy ilyen eljárás háromszori hivatkozást igényelne a táblázatokra. Z. Leonelli 1802-ben táblázatokat közölt az ún. Gauss-logaritmusok– az összegek és különbségek összeadására szolgáló logaritmusok – amelyek lehetővé tették, hogy a táblákhoz egy hozzáférésre korlátozódjunk.

I. Kepler 1624-ben javasolta az arányos logaritmusok táblázatait, i.e. számok logaritmusai a/x, Ahol a– valamilyen pozitív állandó érték. Ezeket a táblázatokat elsősorban csillagászok és navigátorok használják.

Arányos logaritmusok at a= 1-et hívnak cologaritmusokés számításokhoz használják, amikor szorzatokkal és hányadosokkal kell foglalkozni. Egy szám kologaritmusa n egyenlő a reciprok szám logaritmusával; azok. colog n= log1/ n= – log n. Ha log2 = 0,3010, akkor colog2 = – 0,3010 = 0,6990 – 1. A kologaritmusok használatának előnye, hogy az olyan kifejezések logaritmusának kiszámításakor, mint pl. pq/r a pozitív tizedesjegyek hármas összege p+ napló q+kölg r könnyebb megtalálni, mint a vegyes összeg és különbség naplót p+ napló q–napló r.

Sztori.

A logaritmusrendszerek alapelve nagyon régóta ismert, és az ókori babiloni matematikára vezethető vissza (i. e. 2000 körül). Akkoriban a kamatos kamat kiszámításához az egész számok pozitív egész hatványainak táblázatértékei közötti interpolációt használták. Jóval később Arkhimédész (Kr. e. 287–212) 108-as erejét használta, hogy megtalálja az akkor ismert Univerzum teljes kitöltéséhez szükséges homokszemek számának felső határát. Arkhimédész felhívta a figyelmet a kitevők azon tulajdonságára, amely a logaritmusok hatékonyságának hátterében áll: a hatványok szorzata a kitevők összegének felel meg. A középkor végén és a modern kor elején a matematikusok egyre inkább a geometriai és az aritmetikai progresszió kapcsolatára kezdtek fordulni. M. Stiefel esszéjében Integer Aritmetika(1544) táblázatot adott a 2-es szám pozitív és negatív hatványairól:

Stiefel észrevette, hogy az első sorban (a kitevő sorában) lévő két szám összege egyenlő az alsó sorban (a kitevő sorában) lévő két megfelelő szám szorzatának megfelelő kettő kitevőjével. Ezzel a táblázattal kapcsolatban Stiefel négy szabályt fogalmazott meg, amelyek egyenértékűek a kitevőkkel végzett műveletek négy modern szabályával vagy a logaritmusok műveleteinek négy szabályával: a felső sorban szereplő összeg az alsó sorban lévő szorzatnak felel meg; a felső sorban lévő kivonás az alsó sorban lévő osztásnak felel meg; a felső sorban a szorzás az alsó sorban lévő hatványozásnak felel meg; felosztás a felső sorban az alsó sorban történő gyökeresedésnek felel meg.

Nyilvánvalóan Stiefel szabályaihoz hasonló szabályok késztették J. Napert arra, hogy munkájában formálisan bevezesse az első logaritmusrendszert. A logaritmusok csodálatos táblázatának leírása Napier gondolatait azonban a termékek összegekké alakításának problémája foglalkoztatta azóta, hogy több mint tíz évvel munkája megjelenése előtt Napier hírt kapott Dániából, hogy a Tycho Brahe Obszervatóriumban asszisztenseinek olyan módszerük van, lehetséges a termékek összegekké alakítása. A Napier által kapott üzenetben tárgyalt módszer olyan trigonometrikus képletek használatán alapult, mint pl

ezért a Naper-táblázatok főleg trigonometrikus függvények logaritmusaiból álltak. Bár a bázis fogalma nem szerepelt kifejezetten a Napier által javasolt definícióban, az ő rendszerében a logaritmusrendszer bázisával egyenértékű szerepet az (1 – 10 –7)ґ10 7 szám játszotta, amely megközelítőleg egyenlő 1/ e.

Napertől függetlenül és vele szinte egyidejűleg J. Bürgi talált ki és adott ki Prágában egy meglehetősen hasonló típusú logaritmusrendszert, amelyet 1620-ban adtak ki. Aritmetikai és geometriai progressziós táblázatok. Ezek az antilogaritmusok táblázatai voltak az alaphoz (1 + 10 –4) ґ10 4, ami elég jó közelítés a számhoz. e.

A Naper-rendszerben a 10 7 szám logaritmusát nullának vették, és ahogy a számok csökkentek, a logaritmusok növekedtek. Amikor G. Briggs (1561–1631) meglátogatta Napier-t, mindketten egyetértettek abban, hogy kényelmesebb lenne a 10-es számot használni, és az egyes logaritmusát nullának tekinteni. Aztán a számok növekedésével a logaritmusuk növekedni fog. Így megkaptuk a decimális logaritmusok modern rendszerét, amelynek táblázatát Briggs publikálta munkájában Logaritmikus aritmetika(1620). Logaritmus az alaphoz e, bár nem éppen a Naper által bevezetetteket, gyakran Naper-nek nevezik. A "karakterisztikus" és a "mantissza" kifejezéseket Briggs javasolta.

Az első logaritmusok történelmi okokból közelítéseket használtak a számokhoz 1/ eÉs e. Valamivel később a természetes logaritmusok gondolatát a hiperbola alatti területek tanulmányozásával kezdték összekapcsolni. xy= 1 (1. ábra). A 17. században kimutatták, hogy az e görbe által határolt terület, a tengely xés ordináták x= 1 és x = a(az 1. ábrán ezt a területet merészebb és ritkább pontok borítják) növekszik az aritmetikai progresszió, ha a exponenciálisan növekszik. Pontosan ez a függőség merül fel a kitevőkkel és logaritmusokkal végzett műveletek szabályaiban. Emiatt a naperi logaritmusokat „hiperbolikus logaritmusoknak” nevezték.

Logaritmikus függvény.

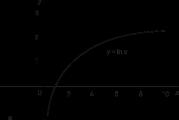
Volt idő, amikor a logaritmusokat kizárólag számítási eszköznek tekintették, de a 18. században, elsősorban Euler munkásságának köszönhetően, kialakult a logaritmikus függvény fogalma. Egy ilyen függvény grafikonja y= log xábrán látható, amelynek ordinátái aritmetikai sorozatban nőnek, míg az abszcisszái geometriai sorozatban nőnek. 2, A. Inverz vagy exponenciális függvény grafikonja y = e xábrán mutatjuk be, amelynek ordinátái nőnek a geometriai progresszióban, és amelyek abszcisszái nőnek a számtani progresszióban. 2, b. (Görbék y=napló xÉs y = 10x alakja hasonló a ívekhez y= log xÉs y = e x.) A logaritmikus függvény alternatív definícióit is javasolták, pl.

kpi ; és ehhez hasonlóan a -1 szám természetes logaritmusai a (2) alakú komplex számok k + 1)pi, Ahol k– egész szám. Hasonló állítások igazak az általános logaritmusokra vagy más logaritmusrendszerekre. Ezenkívül a logaritmus definíciója általánosítható az Euler-azonosságok segítségével, hogy magában foglalja a komplex számok összetett logaritmusait is.

A logaritmikus függvény alternatív definícióját a funkcionális analízis adja. Ha f(x) – valós szám folytonos függvénye x, amely a következő három tulajdonsággal rendelkezik: f (1) = 0, f (b) = 1, f (uv) = f (u) + f (v), Ez f(x) a szám logaritmusa x alapján b. Ez a meghatározás számos előnnyel rendelkezik a cikk elején megadott meghatározáshoz képest.

Alkalmazások.

A logaritmusokat eredetileg kizárólag a számítások egyszerűsítésére használták, és ez az alkalmazás még mindig az egyik legfontosabb alkalmazásuk. A szorzatok, hányadosok, hatványok és gyökök kiszámítását nemcsak a publikált logaritmustáblázatok széles körű elérhetősége segíti elő, hanem az ún. dia szabály - egy számítási eszköz, amelynek működési elve a logaritmus tulajdonságain alapul. A vonalzó logaritmikus skálákkal van felszerelve, azaz. távolság az 1-től bármely számig x loggal egyenlőnek választottuk x; Az egyik skála a másikhoz viszonyított eltolásával lehetőség nyílik a logaritmusok összegeinek vagy különbségeinek ábrázolására, ami lehetővé teszi, hogy a skáláról közvetlenül leolvassuk a megfelelő számok szorzatait vagy hányadosait. Kihasználhatja a számok logaritmikus formában történő ábrázolásának előnyeit is. logaritmikus papír grafikonok ábrázolásához (mindkét koordinátatengelyen logaritmikus skálákkal nyomtatott papír). Ha egy függvény teljesíti az alak hatványtörvényét y = kxn, akkor a logaritmikus gráfja egyenesnek tűnik, mert log y=napló k + n log x– egyenlet lineáris a loghoz képest yés naplózza x. Ellenkezőleg, ha valamely funkcionális függés logaritmikus gráfja egyenesnek tűnik, akkor ez a függőség hatványfüggvény. A félig log papír (ahol az y tengely logaritmikus, az x tengely pedig egységes léptékű) akkor hasznos, ha exponenciális függvényeket kell azonosítani. Az alak egyenletei y = kb rx akkor fordul elő, amikor egy mennyiség, például a lakosság, a radioaktív anyag mennyisége vagy a banki egyenleg a lakosság, a radioaktív anyag vagy a jelenleg rendelkezésre álló pénz mennyiségével arányos mértékben csökken vagy növekszik. Ha egy ilyen függőséget féllogaritmikus papíron ábrázolunk, a grafikon egyenesnek fog kinézni.

A logaritmikus függvény sokféle természeti formával kapcsolatban merül fel. A napraforgóvirágzatban a virágok logaritmikus spirálokba rendeződnek, a puhatestű héjak csavarodnak Nautilus, hegyi juh szarv és papagáj csőr. Mindezek a természetes alakzatok példaként szolgálhatnak egy logaritmikus spirálként ismert görbére, mivel egy poláris koordináta-rendszerben az egyenlete: r = ae bq, vagy ln r= log a + bq. Egy ilyen görbét egy mozgó pont ír le, melynek pólusától mért távolsága mértani haladással növekszik, a sugárvektora által leírt szög pedig aritmetikai haladással növekszik. Egy ilyen görbe, tehát a logaritmikus függvény mindenütt jelenléte jól mutatja, hogy olyan távoli és teljesen eltérő területeken fordul elő, mint egy excentrikus bütyök körvonala és néhány, a fény felé repülő rovar pályája.

Tehát kettős hatalmunk van. Ha az alsó sorból veszi ki a számot, könnyen megtalálhatja azt a teljesítményt, amelyre kettőt kell emelnie, hogy megkapja ezt a számot. Például, hogy 16-ot kapjon, kettőt kell emelnie a negyedik hatványra. És ahhoz, hogy 64-et kapj, kettőt kell emelned a hatodik hatványra. Ez látható a táblázatból.

És most tulajdonképpen a logaritmus meghatározása:

Az x logaritmusának alapja az a hatvány, amelyre a-t fel kell emelni, hogy x-et kapjunk.

Jelölés: log a x = b, ahol a az alap, x az argumentum, b az, amivel a logaritmus valójában egyenlő.

Például 2 3 = 8 ⇒ log 2 8 = 3 (a 8-as 2-es bázis logaritmusa három, mert 2 3 = 8). Ugyanilyen sikerrel log 2 64 = 6, mivel 2 6 = 64.

Egy szám egy adott bázishoz való logaritmusának megtalálását logaritmizálásnak nevezzük. Tehát adjunk hozzá egy új sort a táblázatunkhoz:

2 1	2 2	2 3	2 4	2 5	2 6
2	4	8	16	32	64
log 2 2 = 1	log 2 4 = 2	log 2 8 = 3	log 2 16 = 4	log 2 32 = 5	log 2 64 = 6

Sajnos nem minden logaritmus számítható ki ilyen könnyen. Például próbálja meg megkeresni a log 2 5 értéket. Az 5-ös szám nem szerepel a táblázatban, de a logika azt diktálja, hogy a logaritmus valahol az intervallumon belül legyen. Mert 22< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.

Az ilyen számokat irracionálisnak nevezzük: a tizedesvessző utáni számok a végtelenségig írhatók, és soha nem ismétlődnek. Ha a logaritmus irracionálisnak bizonyul, jobb, ha így hagyjuk: log 2 5, log 3 8, log 5 100.

Fontos megérteni, hogy a logaritmus két változóból álló kifejezés (az alap és az argumentum). Sokan először összekeverik, hol az alap és hol az érv. A bosszantó félreértések elkerülése érdekében csak nézze meg a képet:

[Felirat a képhez]

Előttünk nem más, mint a logaritmus meghatározása. Emlékezik: a logaritmus egy hatvány, amelybe a bázist be kell építeni, hogy argumentumot kapjunk. Ez az alapot, amely hatványra van emelve - a képen pirossal van kiemelve. Kiderült, hogy az alap mindig alul van! Már az első órán elmondom a tanítványaimnak ezt a csodálatos szabályt – és nem keletkezik zavar.

Kitaláltuk a definíciót – már csak az van hátra, hogy megtanuljuk a logaritmusok számolását, azaz megszabadulni a „napló” jelzéstől. Először is megjegyezzük, hogy a meghatározásból két fontos tény következik:

1. Az argumentumnak és az alapnak mindig nagyobbnak kell lennie nullánál. Ez a fok racionális kitevővel történő meghatározásából következik, amelyre a logaritmus definíciója redukálódik.
2. Az alapnak másnak kell lennie, mint az egyiknek, mivel az egyik bármilyen mértékben is az marad. Emiatt értelmetlen a „milyen hatalomra kell emelni az embert, hogy kettőt kapjunk” kérdés. Ilyen végzettség nincs!

Az ilyen korlátozásokat hívják elfogadható értékek tartománya(ODZ). Kiderül, hogy a logaritmus ODZ-je így néz ki: log a x = b ⇒ x > 0, a > 0, a ≠ 1.

Vegye figyelembe, hogy a b számra (a logaritmus értékére) nincs korlátozás. Például a logaritmus lehet negatív is: log 2 0.5 = −1, mert 0,5 = 2 -1.

Most azonban csak numerikus kifejezésekkel foglalkozunk, ahol nem szükséges ismerni a logaritmus VA értékét. Minden korlátozást már figyelembe vettek a feladatok készítői. De amikor a logaritmikus egyenletek és egyenlőtlenségek lépnek életbe, a DL követelmények kötelezővé válnak. Hiszen az alap és az érv nagyon erős konstrukciókat tartalmazhat, amelyek nem feltétlenül felelnek meg a fenti korlátozásoknak.

Most nézzük meg a logaritmusszámítás általános sémáját. Három lépésből áll:

1. Fejezzük ki az a bázist és az x argumentumot olyan hatványként, amelynek minimális lehetséges bázisa nagyobb egynél. Útközben jobb, ha megszabadulunk a tizedesjegyektől;
2. Oldja meg a b változó egyenletét: x = a b ;
3. A kapott b szám lesz a válasz.

Ez minden! Ha a logaritmus irracionálisnak bizonyul, ez már az első lépésben látható lesz. Nagyon fontos az a követelmény, hogy a bázis nagyobb legyen egynél: ez csökkenti a hiba valószínűségét és nagyban leegyszerűsíti a számításokat. Ugyanez a helyzet a tizedes törtekkel: ha azonnal átalakítja őket közönséges törtekre, sokkal kevesebb hiba lesz.

Nézzük meg, hogyan működik ez a séma konkrét példák segítségével:

Feladat. Számítsa ki a logaritmust: log 5 25

1. Képzeljük el az alapot és az argumentumot öt hatványaként: 5 = 5 1 ; 25 = 5 2;
2. Hozzuk létre és oldjuk meg az egyenletet:
   log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2;
3. A választ kaptuk: 2.

Feladat. Számítsa ki a logaritmust:

[Felirat a képhez]

Feladat. Számítsa ki a logaritmust: log 4 64

1. Képzeljük el az alapot és az argumentumot kettő hatványaként: 4 = 2 2 ; 64 = 2 6;
2. Hozzuk létre és oldjuk meg az egyenletet:
   log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3;
3. A választ kaptuk: 3.

Feladat. Számítsa ki a logaritmust: log 16 1

1. Képzeljük el az alapot és az argumentumot kettő hatványaként: 16 = 2 4 ; 1 = 20;
2. Hozzuk létre és oldjuk meg az egyenletet:
   log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0;
3. A választ kaptuk: 0.

Feladat. Számítsa ki a logaritmust: log 7 14

1. Képzeljük el az alapot és az argumentumot hét hatványaként: 7 = 7 1 ; A 14 nem ábrázolható hét hatványaként, mivel a 7 1< 14 < 7 2 ;
2. Az előző bekezdésből az következik, hogy a logaritmus nem számít;
3. A válasz nem változik: napló 7 14.

Egy kis megjegyzés az utolsó példához. Hogyan lehet biztos abban, hogy egy szám nem egy másik szám pontos hatványa? Nagyon egyszerű – csak vegye figyelembe az elsődleges tényezőkben. És ha az ilyen tényezők nem gyűjthetők hatványokba azonos kitevőkkel, akkor az eredeti szám nem pontos hatvány.

Feladat. Nézze meg, hogy a számok pontos hatványok-e: 8; 48; 81; 35; 14.

8 = 2 · 2 · 2 = 2 3 - pontos fok, mert csak egy szorzó van;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 - nem pontos hatvány, mivel két tényező van: 3 és 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 - pontos fok;
35 = 7 · 5 - ismét nem pontos hatvány;
14 = 7 · 2 - megint nem pontos fok;

Vegye figyelembe azt is, hogy maguk a prímszámok mindig önmaguk pontos hatványai.

Tizedes logaritmus

Egyes logaritmusok olyan gyakoriak, hogy különleges nevük és szimbólumuk van.

Az x decimális logaritmusa a 10-es alapú logaritmus, azaz. Az a hatvány, amelyre a 10-et fel kell emelni, hogy megkapjuk az x számot. Megnevezés: lg x.

Például log 10 = 1; lg 100 = 2; lg 1000 = 3 - stb.

Mostantól kezdve, amikor egy olyan kifejezés jelenik meg egy tankönyvben, mint a „Find lg 0.01”, tudd, hogy ez nem elírás. Ez egy decimális logaritmus. Ha azonban nem ismeri ezt a jelölést, bármikor átírhatja:
log x = log 10 x

Minden, ami igaz a közönséges logaritmusokra, igaz a decimális logaritmusokra is.

Természetes logaritmus

Van egy másik logaritmus, amelynek megvan a maga jelölése. Bizonyos szempontból ez még a decimálisnál is fontosabb. A természetes logaritmusról beszélünk.

Az x természetes logaritmusa az e bázis logaritmusa, azaz. az a hatvány, amelyre az e számot fel kell emelni, hogy megkapjuk az x számot. Megnevezés: ln x .

Sokan kérdezik: mi az e szám? Ez egy irracionális szám, pontos értéke nem található és nem írható le. Csak az első számokat közlöm:
e = 2,718281828459...

Nem részletezzük, mi ez a szám, és miért van rá szükség. Ne feledje, hogy e a természetes logaritmus alapja:
ln x = log e x

így ln e = 1; ln e 2 = 2; ln e 16 = 16 - stb. Másrészt ln 2 irracionális szám. Általában bármely racionális szám természetes logaritmusa irracionális. Kivéve persze egyet: ln 1 = 0.

A természetes logaritmusokra a közönséges logaritmusokra érvényes összes szabály érvényes.

Fontos számunkra az Ön személyes adatainak védelme. Emiatt kidolgoztunk egy adatvédelmi szabályzatot, amely leírja, hogyan használjuk és tároljuk az Ön adatait. Kérjük, tekintse át adatvédelmi gyakorlatunkat, és tudassa velünk, ha kérdése van.

Személyes adatok gyűjtése és felhasználása

A személyes adatok olyan adatokra vonatkoznak, amelyek felhasználhatók egy adott személy azonosítására vagy kapcsolatfelvételre.

Amikor kapcsolatba lép velünk, bármikor megkérhetjük személyes adatainak megadására.

Az alábbiakban bemutatunk néhány példát arra, hogy milyen típusú személyes adatokat gyűjthetünk, és hogyan használhatjuk fel ezeket az információkat.

Milyen személyes adatokat gyűjtünk:

• Amikor jelentkezést nyújt be az oldalon, különféle információkat gyűjthetünk, beleértve az Ön nevét, telefonszámát, e-mail címét stb.

Hogyan használjuk fel személyes adatait:

• Az általunk gyűjtött személyes adatok lehetővé teszik számunkra, hogy egyedi ajánlatokkal, promóciókkal és egyéb eseményekkel és közelgő eseményekkel kapcsolatba léphessünk Önnel.
• Időről időre felhasználhatjuk személyes adatait fontos értesítések és közlemények küldésére.
• A személyes adatokat belső célokra is felhasználhatjuk, például auditok lefolytatására, adatelemzésre és különféle kutatásokra annak érdekében, hogy javítsuk szolgáltatásainkat, és javaslatokat adjunk Önnek szolgáltatásainkkal kapcsolatban.
• Ha nyereményjátékban, versenyben vagy hasonló promócióban vesz részt, az Ön által megadott információkat felhasználhatjuk az ilyen programok lebonyolítására.

Információk közlése harmadik fél számára

Az Öntől kapott információkat nem adjuk ki harmadik félnek.

Kivételek:

• Szükség esetén - a törvénynek, a bírósági eljárásnak, a bírósági eljárásoknak megfelelően és/vagy az Orosz Föderáció területén található állami kérelmek vagy kormányzati hatóságok kérelmei alapján - az Ön személyes adatainak nyilvánosságra hozatala. Felfedhetünk Önnel kapcsolatos információkat is, ha úgy ítéljük meg, hogy az ilyen nyilvánosságra hozatal biztonsági, bűnüldözési vagy egyéb közérdekű célból szükséges vagy megfelelő.
• Átszervezés, egyesülés vagy eladás esetén az általunk gyűjtött személyes adatokat átadhatjuk a megfelelő jogutód harmadik félnek.

Személyes adatok védelme

Óvintézkedéseket teszünk – beleértve az adminisztratív, technikai és fizikai intézkedéseket is –, hogy megvédjük személyes adatait az elvesztéstől, lopástól és visszaéléstől, valamint a jogosulatlan hozzáféréstől, nyilvánosságra hozataltól, megváltoztatástól és megsemmisítéstől.

A magánélet tiszteletben tartása vállalati szinten

Személyes adatai biztonságának biztosítása érdekében az adatvédelmi és biztonsági előírásokat közöljük alkalmazottainkkal, és szigorúan betartjuk az adatvédelmi gyakorlatokat.

\(a^(b)=c\) \(\balra jobbra nyíl\) \(\log_(a)(c)=b\)

Magyarázzuk meg egyszerűbben. Például a \(\log_(2)(8)\) egyenlő azzal a hatvánnyal, amelyre a \(2\)-t fel kell emelni, hogy \(8\) legyen. Ebből világosan látszik, hogy \(\log_(2)(8)=3\).

Példák:		\(\log_(5)(25)=2\)		mert \(5^(2)=25\)
		\(\log_(3)(81)=4\)		mert \(3^(4)=81\)
		\(\log_(2)\)\(\frac(1)(32)\) \(=-5\)		mert \(2^(-5)=\)\(\frac(1)(32)\)

A logaritmus argumentuma és alapja

Bármely logaritmusnak a következő „anatómiája” van:

A logaritmus argumentumát általában a szintjén írják, az alapot pedig a logaritmusjelhez közelebbi alsó indexben írják. Ez a bejegyzés pedig így hangzik: „huszonöt logaritmusa az alapöthöz”.

Hogyan kell logaritmust számolni?

A logaritmus kiszámításához meg kell válaszolni a kérdést: milyen hatványra kell emelni az alapot, hogy megkapjuk az argumentumot?

Például, számítsa ki a logaritmust: a) \(\log_(4)(16)\) b) \(\log_(3)\)\(\frac(1)(3)\) c) \(\log_(\) sqrt (5))(1)\) d) \(\log_(\sqrt(7))(\sqrt(7))\) e) \(\log_(3)(\sqrt(3))\)

a) Milyen hatványra kell emelni a \(4\)-t, hogy \(16\) legyen? Nyilván a második. Ezért:

\(\log_(4)(16)=2\)

\(\log_(3)\)\(\frac(1)(3)\) \(=-1\)

c) Milyen hatványra kell emelni a \(\sqrt(5)\) értéket, hogy \(1\) legyen? Milyen erő teszi bármelyiket első számúvá? Nulla, persze!

\(\log_(\sqrt(5))(1)=0\)

d) Milyen hatványra kell emelni a \(\sqrt(7)\) értéket, hogy megkapjuk a \(\sqrt(7)\) értéket? Először is, bármely szám az első hatványhoz egyenlő önmagával.

\(\log_(\sqrt(7))(\sqrt(7))=1\)

e) Milyen hatványra kell emelni a \(3\) értéket, hogy \(\sqrt(3)\) legyen? Tudjuk, hogy ez egy tört hatvány, ami azt jelenti, hogy a négyzetgyök a \(\frac(1)(2)\) hatványa.

\(\log_(3)(\sqrt(3))=\)\(\frac(1)(2)\)

Példa : A logaritmus kiszámítása \(\log_(4\sqrt(2))(8)\)

Megoldás :

\(\log_(4\sqrt(2))(8)=x\)		Meg kell találnunk a logaritmus értékét, jelöljük x-el. Most használjuk a logaritmus definícióját: \(\log_(a)(c)=b\) \(\balra jobbra nyíl\) \(a^(b)=c\)
\((4\sqrt(2))^(x)=8\)		Mi köti össze a \(4\sqrt(2)\)-t és a \(8\)-t? Kettő, mert mindkét szám kettesével ábrázolható: \(4=2^(2)\) \(\sqrt(2)=2^(\frac(1)(2))\) \(8=2^(3)\)
\(((2^(2)\cdot2^(\frac(1)(2))))^(x)=2^(3)\)		A bal oldalon a fokozat tulajdonságait használjuk: \(a^(m)\cdot a^(n)=a^(m+n)\) és \((a^(m))^(n)= a^(m\cdot n)\)
\(2^(\frac(5)(2)x)=2^(3)\)		Az alapok egyenlőek, áttérünk a mutatók egyenlőségére
\(\frac(5x)(2)\) \(=3\)		Szorozzuk meg az egyenlet mindkét oldalát \(\frac(2)(5)\-vel
		A kapott gyök a logaritmus értéke

Válasz : \(\log_(4\sqrt(2))(8)=1,2\)

Miért találták ki a logaritmust?

Ennek megértéséhez oldjuk meg az egyenletet: \(3^(x)=9\). Csak párosítsa az \(x\) karaktert, hogy az egyenlőség működjön. Természetesen \(x=2\).

Most oldja meg az egyenletet: \(3^(x)=8\). Mit egyenlő x? Ez a lényeg.

A legokosabbak azt mondják: "X valamivel kevesebb, mint kettő." Hogyan kell pontosan írni ezt a számot? A kérdés megválaszolására találták ki a logaritmust. Neki köszönhetően itt a válasz így írható fel: \(x=\log_(3)(8)\).

Szeretném hangsúlyozni, hogy a \(\log_(3)(8)\), tetszik minden logaritmus csak egy szám. Igen, szokatlannak tűnik, de rövid. Mert ha tizedesként akarnánk írni, akkor ez így nézne ki: \(1.892789260714.....\)

Példa : Oldja meg a \(4^(5x-4)=10\) egyenletet

Megoldás :

\(4^(5x-4)=10\)		\(4^(5x-4)\) és \(10\) nem hozható ugyanarra a bázisra. Ez azt jelenti, hogy nem nélkülözheti a logaritmust. Használjuk a logaritmus definícióját: \(a^(b)=c\) \(\balra jobbra nyíl\) \(\log_(a)(c)=b\)
\(\log_(4)(10)=5x-4\)		Fordítsuk meg az egyenletet úgy, hogy X legyen a bal oldalon
\(5x-4=\log_(4)(10)\)		Előttünk. Mozgassuk a \(4\) jelet jobbra. És ne félj a logaritmustól, kezeld úgy, mint egy közönséges számot.
\(5x=\log_(4)(10)+4\)		Osszuk el az egyenletet 5-tel
\(x=\)\(\frac(\log_(4)(10)+4)(5)\)		Ez a mi gyökerünk. Igen, szokatlannak tűnik, de nem választják a választ.

Válasz : \(\frac(\log_(4)(10)+4)(5)\)

Tizedes és természetes logaritmus

A logaritmus definíciójának megfelelően az alapja bármely pozitív szám lehet, kivéve egy \((a>0, a\neq1)\). És az összes lehetséges alap között van két olyan gyakran előforduló, hogy egy speciális rövid jelölést találtak ki a logaritmusokhoz:

Természetes logaritmus: olyan logaritmus, amelynek alapja az Euler-szám \(e\) (megközelítőleg \(2,7182818…\)), a logaritmus pedig \(\ln(a)\).

vagyis \(\ln(a)\) ugyanaz, mint \(\log_(e)(a)\)

Tizedes logaritmus: A 10-es bázisú logaritmus \(\lg(a)\) lesz írva.

vagyis \(\lg(a)\) ugyanaz, mint \(\log_(10)(a)\), ahol \(a\) valamilyen szám.

Alapvető logaritmikus azonosság

A logaritmusoknak számos tulajdonsága van. Az egyiket „alaplogaritmikus identitásnak” hívják, és így néz ki:

\(a^(\log_(a)(c))=c\)

Ez a tulajdonság közvetlenül következik a definícióból. Lássuk, pontosan hogyan is jött létre ez a képlet.

Emlékezzünk vissza a logaritmus definíciójának egy rövid jelölésére:

ha \(a^(b)=c\), akkor \(\log_(a)(c)=b\)

Vagyis a \(b\) megegyezik a \(\log_(a)(c)\-vel. Ekkor az \(a^(b)=c\) képletbe \(\log_(a)(c)\)-t írhatunk \(b\) helyett. Kiderült, hogy \(a^(\log_(a)(c))=c\) - a fő logaritmikus azonosság.

A logaritmusok egyéb tulajdonságait is megtalálhatja. Segítségükkel egyszerűsítheti és kiszámíthatja a kifejezések értékeit logaritmusokkal, amelyeket nehéz közvetlenül kiszámítani.

Példa : Keresse meg a \(36^(\log_(6)(5)\) kifejezés értékét

Megoldás :

Válasz : \(25\)

Hogyan írjunk fel egy számot logaritmusként?

Mint fentebb említettük, minden logaritmus csak egy szám. Ez fordítva is igaz: tetszőleges szám felírható logaritmusként. Például tudjuk, hogy \(\log_(2)(4)\) egyenlő kettővel. Ekkor kettő helyett írhat \(\log_(2)(4)\).

De a \(\log_(3)(9)\) egyenlő a \(2\-vel), ami azt jelenti, hogy a \(2=\log_(3)(9)\) -t is írhatjuk. Hasonlóképpen a \(\log_(5)(25)\), és a \(\log_(9)(81)\), stb. Vagyis kiderül

\(2=\log_(2)(4)=\log_(3)(9)=\log_(4)(16)=\log_(5)(25)=\log_(6)(36)=\ log_(7)(49)...\)

Így ha kell, felírhatunk kettőt logaritmusként tetszőleges bázissal bárhol (legyen az egyenletben, kifejezésben vagy egyenlőtlenségben) - az alapot egyszerűen négyzetbe írjuk argumentumként.

Ugyanez a helyzet a triplával – írható \(\log_(2)(8)\), vagy \(\log_(3)(27)\), vagy \(\log_(4)( 64) \)... Ide írjuk be argumentumként az alapot a kockába:

\(3=\log_(2)(8)=\log_(3)(27)=\log_(4)(64)=\log_(5)(125)=\log_(6)(216)=\ log_(7)(343)...\)

És néggyel:

\(4=\log_(2)(16)=\log_(3)(81)=\log_(4)(256)=\log_(5)(625)=\log_(6)(1296)=\ log_(7)(2401)...\)

És mínusz 1-gyel:

\(-1=\) \(\log_(2)\)\(\frac(1)(2)\) \(=\) \(\log_(3)\)\(\frac(1)( 3)\) \(=\) \(\log_(4)\)\(\frac(1)(4)\) \(=\) \(\log_(5)\)\(\frac(1) )(5)\) \(=\) \(\log_(6)\)\(\frac(1)(6)\) \(=\) \(\log_(7)\)\(\frac (1) (7)\) \(...\)

És egyharmaddal:

\(\frac(1)(3)\) \(=\log_(2)(\sqrt(2))=\log_(3)(\sqrt(3))=\log_(4)(\sqrt( 4))=\log_(5)(\sqrt(5))=\log_(6)(\sqrt(6))=\log_(7)(\sqrt(7))...\)

Bármely \(a\) szám logaritmusként ábrázolható \(b\) bázissal: \(a=\log_(b)(b^(a))\)

Példa : Keresse meg a kifejezés jelentését \(\frac(\log_(2)(14))(1+\log_(2)(7))\)

Megoldás :

Válasz : \(1\)

Mi az a logaritmus?

Figyelem!
Vannak további
az 555. külön szakaszban szereplő anyagok.
Azoknak, akik nagyon "nem nagyon..."
És azoknak, akik „nagyon…”)

Mi az a logaritmus? Hogyan lehet logaritmusokat megoldani? Ezek a kérdések sok diplomát megzavarnak. A logaritmus témáját hagyományosan összetettnek, érthetetlennek és ijesztőnek tartják. Főleg a logaritmusos egyenletek.

Ez abszolút nem igaz. Teljesen! Ne higgy nekem? Bírság. Most mindössze 10-20 perc alatt:

1. Meg fogod érteni mi az a logaritmus.

2. Tanuljon meg egy egész osztály exponenciális egyenletet megoldani. Még ha nem is hallottál róluk semmit.

3. Ismerje meg az egyszerű logaritmusok kiszámítását.

Sőt, ehhez csak a szorzótáblát kell ismerned, és azt, hogyan emelhetsz egy számot hatványra...

Úgy érzem, kétségei vannak... Nos, oké, jelölje meg az időt! Megy!

Először fejben oldja meg ezt az egyenletet:

Ha tetszik ez az oldal...

Egyébként van még néhány érdekes oldalam az Ön számára.)

Gyakorolhatod a példák megoldását, és megtudhatod a szintedet. Tesztelés azonnali ellenőrzéssel. Tanuljunk – érdeklődéssel!)

Megismerkedhet a függvényekkel, deriváltokkal.