1. Axialschnitt Zylinder ist ein Abschnitt des Zylinders durch eine Ebene, die durch seine Achse verläuft. Der axiale Querschnitt des Zylinders beträgt Rechteck.

2. Abschnitt eines Zylinders mit einer Ebene parallel zur Basis.
In diesem Fall ist der Querschnitt ein Kreis, der gleich und parallel zur Grundfläche ist.

Kegel

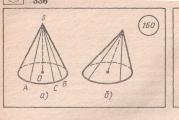
Ein Kegel ist ein geometrischer Körper, der aus einem Kreis besteht – Gründe Kegel, ein Punkt, der nicht in der Ebene dieses Kreises liegt, − Gipfel Kegel und alle Segmente, die die Spitze des Kegels mit den Spitzen der Basis verbinden.

Die Segmente, die den Scheitelpunkt des Kegels mit den Punkten des Grundkreises verbinden, werden genannt Bildung Kegel

Der Kegel heißt Direkte, wenn die gerade Linie, die die Spitze des Kegels mit der Mitte der Basis verbindet, senkrecht zur Ebene der Basis steht.

An Reis. A) gerader Kegel, B) geneigter Kegel.

Im Folgenden betrachten wir nur einen geraden Kegel!

S- die Spitze des Kegels.

Kreis mit Mittelpunkten UM– die Basis des Kegels.

S.A.,C.B., SC– Kegel formen.

Höhe eines Kegels wird die Senkrechte genannt, die von seiner Spitze zur Ebene der Grundfläche absteigt.

Achse eines Kegels ist eine Gerade, die seine Höhe enthält ( ALSO).

Kegeleigenschaften:

Die Generatoren des Kegels sind gleich.

Ein Kegel kann als ein Körper betrachtet werden, der durch Drehen eines rechtwinkligen Dreiecks um seine Seite entsteht.

Die einfachsten Abschnitte eines Kegels.

1. Axialschnitt Kegel ist ein Abschnitt eines Kegels durch eine Ebene, die durch seine Achse verläuft. Der axiale Abschnitt des Kegels beträgt Dreieck.

2. Abschnitt eines Kegels mit einer Ebene parallel zur Basis.
In diesem Fall ist der Querschnitt ein Kreis ähnlich und parallel zur Grundfläche.

Eine Kugel ist ein geometrischer Körper, der aus allen Punkten im Raum besteht, die sich in einem Abstand befinden, der nicht größer als ein bestimmter Wert von einem bestimmten Punkt ist.

Dieser Punkt ( UM) wird genannt Center Ball, und dieser Abstand ist Radius Ball.

Die Grenze des Balls wird genannt sphärische Oberfläche oder Kugel.

Jedes Segment, das den Mittelpunkt einer Kugel mit einem Punkt auf der Kugeloberfläche verbindet, heißt Radius Kugel ( Außendurchmesser, OB, OA).

Kugeldurchmesser ist ein Segment, das zwei Punkte einer Kugeloberfläche verbindet und durch den Mittelpunkt der Kugel verläuft ( AB).

Balleigenschaften:

Die Radien der Kugel sind gleich;

Die Durchmesser der Kugeln sind gleich.

Eine Kugel kann als ein Körper betrachtet werden, der durch Drehen eines Halbkreises um seinen Durchmesser entsteht.

Die einfachsten Abschnitte einer Kugel

1. Schnitt einer Kugel durch eine Ebene, die durch ihre Mitte verläuft. In diesem Fall ist der Abschnitt großer Kreis.

2. Schnitt einer Kugel durch eine Ebene Nicht durch sein Zentrum geht. In diesem Fall ist der Abschnitt Kreis.

Zylindrische Oberfläche m Eine gerade Linie m, die sich entlang einer Kurve bewegt, beschreibt eine zylindrische Oberfläche. Ist diese Kurve geschlossen, so wird eine geschlossene Zylinderfläche beschrieben. Hat eine geschlossene Kurve die Form eines Kreises, so wird ein Kreiszylinder beschrieben. Wenn die Gerade m senkrecht zur Kurvenebene steht, wird ein gerader Kreiszylinder beschrieben. ZYLINDERTYPEN Elliptischer Zylinder ZYLINDERTYPEN Hyperbolischer Zylinder ZYLINDERTYPEN Parabolischer Zylinder 26.07.2014 6 Definition eines Zylinders. Ein Zylinder ist ein Körper, der aus zwei Kreisen besteht, die nicht in derselben Ebene liegen und durch Parallelverschiebung kombiniert werden, und allen Segmenten, die die entsprechenden Punkte dieser Kreise verbinden. Zylinder Ein Zylinder kann durch Drehen eines Rechtecks ​​um eine gerade Linie erhalten werden, die beliebige seiner Seiten enthält. Der Radius eines Zylinders ist der Radius seiner Basis. Die Höhe eines Zylinders ist der Abstand zwischen den Ebenen seiner Grundflächen. Die Achse eines Zylinders ist eine gerade Linie, die durch die Mittelpunkte der Grundflächen verläuft. Eigenschaften des Zylinders. 1) Die Basen sind gleich und parallel. 2) Alle Erzeugenden des Zylinders sind parallel und gleich zueinander. Entwicklung des Zylinders Die Mantelfläche des Zylinders entwickelt sich zu einem Rechteck, dessen eine Seite die Höhe des Zylinders und die andere die Länge des Grundumfangs darstellt . Ein gleichseitiger Zylinder ist ein Zylinder, dessen axialer Querschnitt dem quadratischen Querschnitt des Zylinders entspricht. Der Querschnitt eines Zylinders mit einer Ebene parallel zu seiner Achse ist ein Rechteck. Seine beiden Seiten sind Erzeugende des Zylinders und die anderen beiden sind parallele Sehnen der Basen. Der durch die Zylinderachse verlaufende Abschnitt des Zylinders wird Axialschnitt genannt und ist auch ein Rechteck. Eine Ebene parallel zur Ebene der Grundfläche des Zylinders schneidet seine Mantelfläche entlang eines Kreises, der dem Umfang der Grundfläche entspricht. Tangentenebene Wenn eine Ebene mit der Mantelfläche eine gemeinsame Gerade hat, dann wird diese Ebene Tangentenebene genannt. Die Tangentiallinie ist die Erzeugende des Zylinders. Die Mantelfläche des Zylinders ist ein Rechteck, dessen eine Seite die Höhe des Zylinders und die andere den Umfang darstellt. Die gesamte Oberfläche des Zylinders besteht aus zwei Kreisen und einer Seitenfläche. L H 2 RH S Seitenfläche des Zylinders und S des Kreises R 2 R 2 RH 2 R (R H) 2 S des Kreises S Seitenfläche S volle Oberfläche von Zylinder 2 und Oberfläche von Zylinder 2 und Volumen des Zylinders Das Volumen von Der Zylinder ist gleich dem Produkt aus Grundfläche und Höhe des Zylinders. V S Basis V R 2 H H Erklären Sie, was ein gerader Kreiszylinder ist? Wie groß sind Radius, Höhe, Erzeugende und Achse des Zylinders? Was ist der Axialschnitt eines Zylinders? Welcher Zylinder heißt gleichseitig? Wie groß ist der Schnitt eines Zylinders durch eine Ebene senkrecht zur Zylinderachse? Was verstehen wir unter der Mantel- und Gesamtfläche des Zylinders? Wie finde ich die Seiten- und Gesamtoberfläche eines Zylinders? ELEMENTE EINES ZYLINDERS Problem 1. Der axiale Abschnitt eines Zylinders ist ein Quadrat, dessen Fläche Q ist. Finden Sie die Fläche der Basis des Zylinders. Gegeben: Zylinder, Axialschnitt - Quadrat SAbschnitt = Q Finden: Sbas = Kreis Lösung: Aufgabe 2. Die Mantelfläche des Zylinders verwandelt sich in ein Quadrat mit einer Fläche von 4 cm2. Ermitteln Sie die Gesamtoberfläche und das Gesamtvolumen des Zylinders. Angenommen 3 N lKreis Gegeben: Zylinderquadrat = 4 cm2 Gefunden: Sp.p., Vcyl. Lösung: Labor- und Praxisarbeit Thema: Zylinder 1. Definition, Eigenschaften. 2. Zeichnung, Maße in mm. 3. Berechnen Sie: a) Grundfläche b) Mantelfläche des Zylinders. c) die gesamte Oberfläche des Zylinders. d) Volumen des Zylinders. Probleme Die Diagonale des Axialschnitts beträgt 48 cm. Der Winkel zwischen der Diagonale und der Erzeugenden des Zylinders beträgt 60°. Finden Sie 1) die Höhe des Zylinders; 2) Radius des Zylinders; 3) Sbas Die Höhe des Zylinders beträgt 8 cm, der Radius beträgt 5 cm. Ermitteln Sie die Querschnittsfläche einer Ebene parallel zu ihrer Achse, wenn der Abstand zwischen dieser Ebene und der Achse des Zylinders 3 cm beträgt. Die Fläche der Mantelfläche des Zylinders beträgt S. Ermitteln Sie den axialen Querschnitt. Querschnittsfläche des Zylinders. Den Zylinder erhält man, indem man ein Quadrat mit der Seite α um eine seiner Seiten dreht. Finden Sie die Fläche von: 1) dem axialen Abschnitt des Zylinders; 2) die volle Oberfläche des Zylinders Zylinder Originalität in Design und Architektur Problem: Wie stark vergrößert sich das Volumen der Brennkammer des GAZ-53-Automotors, wenn der Kolbendurchmesser 10 cm und der Kolbenhub 9 cm beträgt? Lösung V=пR2H: V=3,14 52 9=706,5 (cm3) Problem Bestimmen Sie das Fassungsvermögen des Öltanks der Servolenkungspumpe des ZIL130-Autos, wenn sein Durchmesser 126 mm und seine Höhe 140 mm beträgt. Lösung V=пR2H =3,14. 3969,140=174477,24

Zylinder (gerader Kreiszylinder) ist ein Körper, der aus zwei Kreisen (den Grundflächen eines Zylinders) besteht, die durch Parallelverschiebung verbunden werden, und allen Segmenten, die die entsprechenden Punkte dieser Kreise während der Parallelverschiebung verbinden. Die Segmente, die die entsprechenden Punkte der Grundkreise verbinden, werden Erzeuger des Zylinders genannt.

Hier ist eine weitere Definition:

Zylinder- ein Körper, der durch eine zylindrische Oberfläche mit geschlossener Führung und zwei parallelen Ebenen begrenzt wird, die die Erzeugenden dieser Oberfläche schneiden.

Zylindrische Oberfläche- eine Fläche, die durch die Bewegung einer geraden Linie entlang einer bestimmten Kurve entsteht. Die gerade Linie wird als Erzeugende der Zylinderfläche bezeichnet, die gekrümmte Linie als Führung der Zylinderfläche.

Mantelfläche des Zylinders- Teil einer zylindrischen Oberfläche, die durch parallele Ebenen begrenzt wird.

Zylinderbasen- Teile paralleler Ebenen, die von der Seitenfläche des Zylinders abgeschnitten werden.

Abb.1 Mini

Der Zylinder heißt Direkte(Cm. Abb.1), wenn seine Generatoren senkrecht zu den Ebenen der Basen stehen. Ansonsten heißt der Zylinder geneigt.

Runder Zylinder- ein Zylinder, dessen Grundflächen Kreise sind.

Rechter Kreiszylinder (nur ein Zylinder) ist ein Körper, der durch Drehen eines Rechtecks ​​um eine seiner Seiten entsteht. Cm. Abb.1.

Zylinderradius ist der Radius seiner Basis.

Generator des Zylinders- Erzeugende einer Zylinderfläche.

Zylinderhöhe wird der Abstand zwischen den Ebenen der Basen genannt. Zylinderachse eine gerade Linie genannt, die durch die Mittelpunkte der Basen verläuft. Der Schnitt eines Zylinders durch eine Ebene, die durch die Achse des Zylinders verläuft, wird aufgerufen Axialschnitt.

Die Achse des Zylinders verläuft parallel zu seiner Erzeugenden und ist die Symmetrieachse des Zylinders.

Eine Ebene, die durch die Mantellinie eines geraden Zylinders verläuft und senkrecht zum durch diese Mantellinie gezogenen Axialschnitt verläuft, wird aufgerufen Tangentenebene des Zylinders. Cm. Abb.2.

Entwicklung der Mantelfläche des Zylinders- ein Rechteck mit Seiten gleich der Höhe des Zylinders und dem Umfang der Basis.

Seitenfläche des Zylinders- Entwicklungsbereich der Seitenfläche. $$S_(side)=2\pi\cdot rh$$ , wobei H ist die Höhe des Zylinders und R– Radius der Basis.

Gesamtoberfläche eines Zylinders- Fläche, die gleich der Summe der Flächen der beiden Grundflächen des Zylinders und seiner Seitenfläche ist, d.h. wird durch die Formel ausgedrückt: $$S_(full)=2\pi\cdot r^2 + 2\pi\cdot rh = 2\pi\cdot r(r+h)$$ , wobei H ist die Höhe des Zylinders und R– Radius der Basis.

Volumen eines beliebigen Zylinders gleich dem Produkt aus der Grundfläche und der Höhe: $$V = S\cdot h$$ Volumen eines runden Zylinders: $$V=\pi r^2 \cdot h$$ , wobei ( R- Basisradius).

Ein Prisma ist ein besonderer Zylindertyp (die Generatoren verlaufen parallel zu den Seitenrippen; die Führung ist ein an der Basis liegendes Polygon). Andererseits kann ein beliebiger Zylinder als entartetes („geglättetes“) Prisma mit einer sehr großen Anzahl sehr schmaler Flächen betrachtet werden. In der Praxis ist ein Zylinder nicht von einem solchen Prisma zu unterscheiden. Alle Eigenschaften des Prismas bleiben im Zylinder erhalten.

Stereometrie ist ein Zweig der Geometrie, in dem Figuren im Raum untersucht werden. Die Hauptfiguren im Raum sind ein Punkt, eine Gerade und eine Ebene. In der Stereometrie tritt eine neue Art der relativen Anordnung von Linien auf: sich kreuzende Linien. Dies ist einer der wenigen wesentlichen Unterschiede zwischen Stereometrie und Planimetrie, da in vielen Fällen Probleme in der Stereometrie durch die Betrachtung verschiedener Ebenen gelöst werden, in denen die Planimetriegesetze erfüllt sind.

In der Natur um uns herum gibt es viele Objekte, die physische Modelle dieser Figur sind. Beispielsweise haben viele Maschinenteile die Form eines Zylinders oder sind eine Kombination daraus, und die majestätischen Säulen von Tempeln und Kathedralen in Zylinderform unterstreichen deren Harmonie und Schönheit.

griechisch − Kylindros. Ein alter Begriff. Im Alltag - eine Papyrusrolle, eine Rolle, eine Rolle (Verb – drehen, rollen).

Für Euklid entsteht ein Zylinder durch Drehen eines Rechtecks. In Cavalieri - durch die Bewegung der Generatrix (mit einer willkürlichen Führung - einem „Zylinder“).

Der Zweck dieses Aufsatzes besteht darin, einen geometrischen Körper zu betrachten – einen Zylinder.

Um dieses Ziel zu erreichen, müssen folgende Aufgaben berücksichtigt werden:

− Geben Sie Definitionen eines Zylinders an.

− Betrachten Sie die Elemente des Zylinders;

− Studieren Sie die Eigenschaften des Zylinders;

− Berücksichtigen Sie die Arten von Zylinderabschnitten.

− Leiten Sie die Formel für die Fläche eines Zylinders her;

− Leiten Sie die Formel für das Volumen eines Zylinders her.

− Probleme mit einem Zylinder lösen.

1.1. Definition eines Zylinders

Betrachten wir eine Linie (Kurve, unterbrochen oder gemischt) l, die in einer Ebene α liegt, und eine gerade Linie S, die diese Ebene schneidet. Durch alle Punkte einer gegebenen Geraden l zeichnen wir Geraden parallel zur Geraden S; Die durch diese Geraden gebildete Fläche α wird Zylinderfläche genannt. Die Linie l wird als Führung dieser Fläche bezeichnet, die Linien s 1, s 2, s 3,... sind ihre Erzeuger.

Wenn die Führung gebrochen ist, besteht eine solche zylindrische Oberfläche aus einer Reihe flacher Streifen, die zwischen Paaren paralleler gerader Linien eingeschlossen sind, und wird als prismatische Oberfläche bezeichnet. Die Erzeugenden, die durch die Scheitelpunkte der gestrichelten Führungslinie verlaufen, werden als Kanten der prismatischen Oberfläche bezeichnet, die flachen Streifen dazwischen sind ihre Flächen.

Wenn wir eine beliebige Zylinderfläche mit einer beliebigen Ebene schneiden, die nicht parallel zu ihren Erzeugenden verläuft, erhalten wir eine Linie, die auch als Orientierungslinie für diese Fläche dienen kann. Unter den Führungen sticht diejenige hervor, die man erhält, indem man die Oberfläche mit einer Ebene senkrecht zu den Erzeugenden der Oberfläche schneidet. Ein solcher Abschnitt wird als normaler Abschnitt bezeichnet, und die entsprechende Führung wird als normale Führung bezeichnet.

Wenn die Führung eine geschlossene (konvexe) Linie (gestrichelt oder gekrümmt) ist, wird die entsprechende Fläche als geschlossene (konvexe) prismatische oder zylindrische Fläche bezeichnet. Die einfachste zylindrische Oberfläche hat als normale Führung einen Kreis. Zerlegen wir eine geschlossene konvexe Prismenfläche mit zwei Ebenen parallel zueinander, aber nicht parallel zu den Erzeugenden.

In Abschnitten erhalten wir konvexe Polygone. Nun begrenzen der zwischen den Ebenen α und α“ eingeschlossene Teil der Prismenfläche und die beiden in diesen Ebenen gebildeten Polygonplatten einen Körper, der als prismatischer Körper bezeichnet wird – ein Prisma.

Zylindrischer Körper – ein Zylinder wird ähnlich wie ein Prisma definiert:
Ein Zylinder ist ein Körper, der an den Seiten durch eine geschlossene (konvexe) zylindrische Oberfläche und an den Enden durch zwei flache parallele Grundflächen begrenzt wird. Beide Grundflächen des Zylinders sind gleich, und alle Bestandteile des Zylinders sind ebenfalls gleich, d. h. Segmente der Erzeugenden einer zylindrischen Oberfläche zwischen den Ebenen der Basen.

Ein Zylinder (genauer ein Kreiszylinder) ist ein geometrischer Körper, der aus zwei Kreisen besteht, die nicht in derselben Ebene liegen und durch Parallelverschiebung kombiniert werden, und allen Segmenten, die die entsprechenden Punkte dieser Kreise verbinden (Abb. 1). .

Die Kreise werden als Basen des Zylinders bezeichnet, und die Segmente, die die entsprechenden Punkte des Kreisumfangs verbinden, werden als Generatoren des Zylinders bezeichnet.

Da es sich bei der Parallelverschiebung um eine Bewegung handelt, sind die Grundflächen des Zylinders gleich.

Da sich die Ebene bei der Parallelverschiebung in eine parallele Ebene (oder in sich selbst) verwandelt, liegen die Grundflächen des Zylinders in parallelen Ebenen.

Da bei der Parallelverschiebung die Punkte entlang paralleler (oder zusammenfallender) Linien um den gleichen Abstand verschoben werden, sind die Erzeugenden des Zylinders parallel und gleich.

Die Oberfläche des Zylinders besteht aus Grund- und Seitenfläche. Die Mantelfläche besteht aus Erzeugenden.

Ein Zylinder heißt gerade, wenn seine Erzeugenden senkrecht zu den Grundflächenebenen stehen.

Einen geraden Zylinder kann man sich visuell als einen geometrischen Körper vorstellen, der ein Rechteck beschreibt, wenn man ihn um seine Seite als Achse dreht (Abb. 2).

Reis. 2 − Gerader Zylinder

Im Folgenden betrachten wir nur den geraden Zylinder und nennen ihn der Kürze halber einfach Zylinder.

Der Radius eines Zylinders ist der Radius seiner Basis. Die Höhe eines Zylinders ist der Abstand zwischen den Ebenen seiner Grundflächen. Die Achse eines Zylinders ist eine gerade Linie, die durch die Mittelpunkte der Grundflächen verläuft. Es liegt parallel zu den Generatoren.

Ein Zylinder heißt gleichseitig, wenn seine Höhe gleich dem Durchmesser der Grundfläche ist.

Wenn die Grundflächen des Zylinders flach sind (und daher die sie enthaltenden Ebenen parallel sind), dann sagt man, dass der Zylinder auf einer Ebene steht. Stehen die Grundflächen eines auf einer Ebene stehenden Zylinders senkrecht zur Erzeugenden, so heißt der Zylinder gerade.

Insbesondere wenn die Grundfläche eines auf einer Ebene stehenden Zylinders ein Kreis ist, dann spricht man von einem kreisförmigen (Kreis-)Zylinder; Wenn es eine Ellipse ist, dann ist es elliptisch.

1. 3. Abschnitte des Zylinders

Der Querschnitt eines Zylinders mit einer zu seiner Achse parallelen Ebene ist ein Rechteck (Abb. 3, a). Seine beiden Seiten sind die Generatoren des Zylinders und die anderen beiden sind parallele Sehnen der Basen.

A) B)

V) G)

Reis. 3 – Abschnitte des Zylinders

Insbesondere ist das Rechteck der Axialschnitt. Dies ist ein Abschnitt eines Zylinders, durch dessen Achse eine Ebene verläuft (Abb. 3, b).

Der Querschnitt eines Zylinders mit einer Ebene parallel zur Basis ist ein Kreis (Abbildung 3, c).

Der Querschnitt eines Zylinders mit einer zur Grundfläche nicht parallelen Ebene und einer ovalen Achse (Abb. 3d).

Satz 1. Eine Ebene parallel zur Ebene der Grundfläche des Zylinders schneidet seine Mantelfläche entlang eines Kreises, der dem Umfang der Grundfläche entspricht.

Nachweisen. Sei β eine Ebene parallel zur Ebene der Zylinderbasis. Die parallele Verschiebung in Richtung der Zylinderachse, die die Ebene β mit der Ebene der Basis des Zylinders kombiniert, kombiniert den Abschnitt der Seitenfläche durch die Ebene β mit dem Umfang der Basis. Der Satz ist bewiesen.

Die Mantelfläche des Zylinders.

Als Fläche der Mantelfläche des Zylinders wird die Grenze angenommen, zu der die Fläche der Mantelfläche eines in den Zylinder eingeschriebenen regelmäßigen Prismas tendiert, wenn die Seitenzahl der Basis dieses Prismas auf unbestimmte Zeit zunimmt.

Satz 2. Die Fläche der Mantelfläche eines Zylinders ist gleich dem Produkt aus dem Umfang seiner Basis und seiner Höhe (S side.c = 2πRH, wobei R der Radius der Basis des Zylinders ist, H ist die Höhe des Zylinders).

A) B)
Reis. 4 − Mantelfläche des Zylinders

Nachweisen.

Seien P n und H der Umfang der Basis bzw. die Höhe eines regelmäßigen n-eckigen Prismas, das in den Zylinder eingeschrieben ist (Abb. 4, a). Dann ist die Fläche der Seitenfläche dieses Prismas S Seite.c − P n H. Nehmen wir an, dass die Anzahl der Seiten des in die Basis eingeschriebenen Polygons unbegrenzt wächst (Abb. 4, b). Dann tendiert der Umfang P n zum Umfang C = 2πR, wobei R der Radius der Zylinderbasis ist und sich die Höhe H nicht ändert. Somit tendiert die Fläche der Seitenfläche des Prismas zur Grenze von 2πRH, d. h. die Fläche der Seitenfläche des Zylinders ist gleich S Seite.c = 2πRH. Der Satz ist bewiesen.

Die Gesamtoberfläche des Zylinders.

Die Gesamtoberfläche eines Zylinders ist die Summe der Flächen der Mantelfläche und der beiden Grundflächen. Die Fläche jeder Basis des Zylinders ist gleich πR 2, daher wird die Fläche der Gesamtoberfläche des Zylinders S total nach der Formel S side.c = 2πRH+ 2πR 2 berechnet.

R

T 1

T

F

F 1

F

T

A)

F

B)

Reis. 5 − Gesamtoberfläche des Zylinders

Wenn die Seitenfläche des Zylinders entlang der Erzeugenden FT (Abb. 5, a) geschnitten und so entfaltet wird, dass alle Erzeugenden in derselben Ebene liegen, erhalten wir als Ergebnis ein Rechteck FTT1F1, das als Entwicklung des bezeichnet wird Seitenfläche des Zylinders. Die Seite FF1 des Rechtecks ​​ist die Entwicklung des Grundkreises des Zylinders, daher ist FF1=2πR, und ihre Seite FT ist gleich der Erzeugenden des Zylinders, d. h. FT = H (Abb. 5, b). Somit ist die Fläche FT∙FF1=2πRH der Zylinderentwicklung gleich der Fläche seiner Mantelfläche.

1.5. Zylindervolumen

Wenn ein geometrischer Körper einfach ist, also in endlich viele dreieckige Pyramiden unterteilt werden kann, dann ist sein Volumen gleich der Summe der Volumina dieser Pyramiden. Für einen beliebigen Körper wird das Volumen wie folgt bestimmt.

Ein gegebener Körper hat ein Volumen V, wenn es einfache Körper gibt, die ihn enthalten, und einfache Körper, die in ihm enthalten sind und deren Volumina so wenig wie gewünscht von V abweichen.

Wenden wir diese Definition an, um das Volumen eines Zylinders mit dem Basisradius R und der Höhe H zu ermitteln.

Bei der Ableitung der Formel für die Fläche eines Kreises wurden zwei n-Ecke konstruiert (eines enthält den Kreis, das andere im Kreis enthalten), so dass sich ihre Flächen bei unbegrenzter Zunahme von n der Fläche von näherten der Kreis ohne Grenzen. Konstruieren wir solche Polygone für den Kreis an der Basis des Zylinders. Sei P ein Polygon, das einen Kreis enthält, und P" ein Polygon, das in einem Kreis enthalten ist (Abb. 6).

Reis. 7 − Zylinder mit beschriebenem und beschriftetem Prisma

Konstruieren wir zwei gerade Prismen mit den Grundflächen P und P" und einer Höhe H gleich der Höhe des Zylinders. Das erste Prisma enthält einen Zylinder und das zweite Prisma ist in einem Zylinder enthalten. Denn mit einer unbegrenzten Zunahme von n ist die Flächen der Grundflächen der Prismen nähern sich unbegrenzt der Fläche der Grundfläche des Zylinders S, dann nähern sich ihre Volumina SH gemäß der Definition dem Volumen des Zylinders

V = SH = πR 2 H.

Das Volumen eines Zylinders ist also gleich dem Produkt aus der Grundfläche und der Höhe.

Aufgabe 1.

Der axiale Querschnitt des Zylinders ist ein Quadrat mit der Fläche Q.

Finden Sie die Grundfläche des Zylinders.

Gegeben: Zylinder, Quadrat – Axialschnitt des Zylinders, S Quadrat = Q.

Fundort: S-Hauptzylinder

Die Seite des Quadrats ist . Er entspricht dem Durchmesser der Basis. Daher beträgt die Fläche der Basis .

Antwort: S Hauptzylinder. =

Aufgabe 2.

In einen Zylinder ist ein regelmäßiges sechseckiges Prisma eingeschrieben. Ermitteln Sie den Winkel zwischen der Diagonale seiner Seitenfläche und der Achse des Zylinders, wenn der Radius der Basis gleich der Höhe des Zylinders ist.

Gegeben: Zylinder, regelmäßiges sechseckiges Prisma, das in den Zylinder eingeschrieben ist, Basisradius = Höhe des Zylinders.

Finden Sie: den Winkel zwischen der Diagonale seiner Seitenfläche und der Achse des Zylinders.

Lösung: Die Seitenflächen des Prismas sind Quadrate, da die Seite eines regelmäßigen Sechsecks, das in einen Kreis eingeschrieben ist, gleich dem Radius ist.

Die Kanten des Prismas sind parallel zur Zylinderachse, daher ist der Winkel zwischen der Diagonale der Fläche und der Zylinderachse gleich dem Winkel zwischen der Diagonale und der Seitenkante. Und dieser Winkel beträgt 45°, da die Flächen quadratisch sind.

Antwort: Der Winkel zwischen der Diagonale seiner Seitenfläche und der Achse des Zylinders = 45°.

Aufgabe 3.

Die Höhe des Zylinders beträgt 6 cm, der Radius der Basis beträgt 5 cm.

Finden Sie die Fläche eines parallel zur Zylinderachse gezeichneten Abschnitts in einem Abstand von 4 cm davon.

Gegeben: H = 6 cm, R = 5 cm, OE = 4 cm.

Fundort: S Sek.

S Sek. = KM×KS,

OE = 4 cm, KS = 6 cm.

Dreieck OKM - gleichschenklig (OK = OM = R = 5 cm),

Das Dreieck OEK ist rechtwinklig.

Aus dem Dreieck OEK nach dem Satz des Pythagoras:

KM = 2EK = 2×3 = 6,

S Sek. = 6×6 = 36 cm 2.

Der Zweck dieses Aufsatzes wurde erfüllt; ein geometrischer Körper wie ein Zylinder wurde betrachtet.

Folgende Aufgaben kommen in Betracht:

− die Definition eines Zylinders ist gegeben;

− die Elemente des Zylinders werden berücksichtigt;

− die Eigenschaften des Zylinders wurden untersucht;

− Arten von Zylinderabschnitten werden berücksichtigt;

− die Formel für die Fläche eines Zylinders wird abgeleitet;

− die Formel für das Volumen eines Zylinders wird hergeleitet;

− Probleme mit einem Zylinder gelöst.

1. Pogorelov A.V. Geometrie: Lehrbuch für 10 – 11 Klassen von Bildungseinrichtungen, 1995.

2. Beskin L.N. Stereometrie. Handbuch für Sekundarschullehrer, 1999.

3. Atanasyan L. S., Butuzov V. F., Kadomtsev S. B., Kiseleva L. S., Poznyak E. G. Geometrie: Lehrbuch für die Klassen 10 - 11 von Bildungseinrichtungen, 2000.

4. Aleksandrov A.D., Werner A.L., Ryzhik V.I. Geometrie: Lehrbuch für die Klassen 10-11 in allgemeinbildenden Einrichtungen, 1998.

5. Kiselev A. P., Rybkin N. A. Geometrie: Stereometrie: Klassen 10 – 11: Lehrbuch und Problembuch, 2000.