Logaritmus daného čísla se nazývá exponent, na který je třeba zvýšit další číslo, zavolat základ logaritmus k získání tohoto čísla. Například základní 10 logaritmus 100 je 2. Jinými slovy, 10 musí být odmocněno, aby se dostalo 100 (10 2 = 100). Li n- dané číslo, b– základna a l– tedy logaritmus b l = n. Číslo n také nazývaný základní antilogaritmus bčísla l. Například antilogaritmus 2 k základu 10 je roven 100. To lze zapsat ve formě protokolu vztahů b n = l a antilog b l = n.

Základní vlastnosti logaritmů:

Jakékoli kladné číslo jiné než jedna může sloužit jako základ pro logaritmy, ale bohužel se ukazuje, že pokud b A n jsou racionální čísla, pak ve vzácných případech existuje takové racionální číslo l, Co b l = n. Je však možné definovat iracionální číslo l například takový, že 10 l= 2; toto je iracionální číslo l lze s libovolnou požadovanou přesností aproximovat racionálními čísly. Ukazuje se, že v uvedeném příkladu l je přibližně rovna 0,3010 a tuto aproximaci základního 10 logaritmu 2 lze nalézt ve čtyřmístných tabulkách dekadických logaritmů. Logaritmy se základnou 10 (nebo logaritmy se základnou 10) se ve výpočtech tak běžně používají, že se nazývají obyčejný logaritmy a zapsány jako log2 = 0,3010 nebo log2 = 0,3010, s vynecháním explicitní indikace základu logaritmu. Logaritmy k základně E, transcendentální číslo přibližně rovné 2,71828 přírodní logaritmy. Nacházejí se především v pracích o matematické analýze a jejích aplikacích v různých vědách. Přirozené logaritmy se také píší bez explicitního označení základu, ale pomocí speciálního zápisu ln: například ln2 = 0,6931, protože E 0,6931 = 2.

Použití tabulek obyčejných logaritmů.

Regulární logaritmus čísla je exponent, na který se musí zvýšit 10, aby se získalo dané číslo. Protože 10 0 = 1, 10 1 = 10 a 10 2 = 100, okamžitě dostaneme, že log1 = 0, log10 = 1, log100 = 2 atd. pro rostoucí celočíselné mocniny 10. Stejně tak 10 –1 = 0,1, 10 –2 = 0,01 a tedy log0,1 = –1, log0,01 = –2 atd. pro všechny záporné celočíselné mocniny 10. Obvyklé logaritmy zbývajících čísel jsou uzavřeny mezi logaritmy nejbližších celých mocnin 10; log2 musí být mezi 0 a 1, log20 musí být mezi 1 a 2 a log0.2 musí být mezi -1 a 0. Logaritmus se tedy skládá ze dvou částí, celého čísla a desetinného čísla, uzavřených mezi 0 a 1. volaná celočíselná část charakteristický logaritmus a je určen samotným číslem, nazývá se zlomková část mantisa a lze je zjistit z tabulek. Také log20 = log(2ґ10) = log2 + log10 = (log2) + 1. Logaritmus 2 je 0,3010, takže log20 = 0,3010 + 1 = 1,3010. Podobně log0,2 = log(2®10) = log2 – log10 = (log2) – 1 = 0,3010 – 1. Po odečtení dostaneme log0,2 = – 0,6990. Je však vhodnější reprezentovat log0,2 jako 0,3010 – 1 nebo jako 9,3010 – 10; Lze formulovat i obecné pravidlo: všechna čísla získaná z daného čísla vynásobením mocninou 10 mají shodné mantisy rovné mantise daného čísla. Většina tabulek ukazuje mantisy čísel v rozsahu od 1 do 10, protože mantisy všech ostatních čísel lze získat z čísel uvedených v tabulce.

Většina tabulek uvádí logaritmy se čtyřmi nebo pěti desetinnými místy, ačkoli existují sedmimístné tabulky a tabulky s ještě více desetinnými místy. Nejjednodušší způsob, jak se naučit používat takové tabulky, je pomocí příkladů. Abychom našli log3.59, nejprve si všimneme, že číslo 3,59 je mezi 10 0 a 10 1, takže jeho charakteristika je 0. Najdeme v tabulce číslo 35 (vlevo) a přesuneme se po řádku na sloupec, který má nahoře číslo 9; průsečík tohoto sloupce a řádku 35 je 5551, takže log3,59 = 0,5551. Chcete-li najít mantisu čísla se čtyřmi platnými číslicemi, musíte použít interpolaci. V některých tabulkách je interpolace usnadněna proporcemi uvedenými v posledních devíti sloupcích na pravé straně každé stránky tabulek. Nyní najdeme log736.4; číslo 736,4 leží mezi 10 2 a 10 3, proto je charakteristika jeho logaritmu 2. V tabulce najdeme řádek vlevo od něj 73 a sloupec 6. Na průsečíku tohoto řádku a tohoto sloupce je číslo 8669. Mezi lineárními částmi najdeme sloupec 4 Na průsečíku řádku 73 a sloupce 4 je číslo 2. Přičtením 2 k 8669 dostaneme mantisu - rovná se 8671. Log736,4 = 2,8671.

Přirozené logaritmy.

Tabulky a vlastnosti přirozených logaritmů jsou podobné tabulkám a vlastnostem běžných logaritmů. Hlavní rozdíl mezi oběma je v tom, že celočíselná část přirozeného logaritmu není pro určení polohy desetinné čárky významná, a proto rozdíl mezi mantisou a charakteristikou nehraje zvláštní roli. Přirozené logaritmy čísel 5,432; 54,32 a 543,2 se rovnají 1,6923; 3,9949 a 6,2975. Vztah mezi těmito logaritmy bude zřejmý, vezmeme-li v úvahu rozdíly mezi nimi: log543,2 – log54,32 = 6,2975 – 3,9949 = 2,3026; poslední číslo není nic jiného než přirozený logaritmus čísla 10 (zapsáno takto: ln10); log543,2 – log5,432 = 4,6052; poslední číslo je 2ln10. Ale 543,2 = 10ґ54,32 = 10 2ґ5,432. Tedy přirozeným logaritmem daného čísla A můžete najít přirozené logaritmy čísel rovnající se součinům čísla A pro jakýkoli stupeň nčísla 10 pokud do ln A přidat ln10 násobeno n, tj. ln( Aґ10n) = log A + n ln10 = ln A + 2,3026n. Například ln0,005432 = ln(5,432ґ10 –3) = ln5,432 – 3ln10 = 1,6923 – (3ґ2,3026) = – 5,2155. Proto tabulky přirozených logaritmů, stejně jako tabulky běžných logaritmů, obvykle obsahují pouze logaritmy čísel od 1 do 10. V systému přirozených logaritmů lze mluvit o antilogaritmech, ale častěji se mluví o exponenciální funkci nebo exponentu. Li X= log y, Že y = e x, A y nazýván exponentem X(pro typografické pohodlí často píší y= zk X). Exponent hraje roli antilogaritmu čísla X.

Pomocí tabulek desítkových a přirozených logaritmů můžete vytvářet tabulky logaritmů v jakémkoli jiném základu než 10 a E. Pokud log b a = X, Že b x = A, a proto log c b x=log c a nebo X log c b=log c a nebo X=log c a/log c b=log b a. Proto použijte tento inverzní vzorec ze základní logaritmické tabulky C můžete vytvořit tabulky logaritmů v jakékoli jiné bázi b. Násobitel 1/log c b volal přechodový modul ze základny C na základnu b. Nic nebrání například použití inverzního vzorce nebo přechodu z jednoho systému logaritmů do druhého, nalezení přirozených logaritmů z tabulky běžných logaritmů nebo provedení obráceného přechodu. Například log105.432 = log E 5,432/log E 10 = 1,6923/2,3026 = 1,6923ґ0,4343 = 0,7350. Číslo 0,4343, kterým se musí přirozený logaritmus daného čísla vynásobit, aby se získal obyčejný logaritmus, je modul přechodu do systému obyčejných logaritmů.

Speciální stoly.

Logaritmy byly původně vynalezeny tak, že pomocí jejich vlastností log ab=log A+ log b a log A/b=log A–log b přeměňte produkty na součty a podíly na rozdíly. Jinými slovy, pokud log A a log b jsou známé, pak pomocí sčítání a odčítání můžeme snadno najít logaritmus součinu a kvocientu. V astronomii se však často uvádějí hodnoty log A a log b musím najít log( A + b) nebo log( A – b). Samozřejmě, že by se dalo nejprve najít z tabulek logaritmů A A b, pak proveďte uvedené sčítání nebo odečítání a opět s odkazem na tabulky najděte požadované logaritmy, ale takový postup by vyžadoval odkazovat se na tabulky třikrát. Z. Leonelli v roce 1802 zveřejnil tabulky t. zv. Gaussovy logaritmy– logaritmy pro sčítání součtů a rozdílů – což umožnilo omezit se na jeden přístup k tabulkám.

V roce 1624 navrhl I. Kepler tabulky proporcionálních logaritmů, tzn. logaritmy čísel A/X, Kde A– nějaká kladná konstantní hodnota. Tyto tabulky využívají především astronomové a navigátoři.

Proporcionální logaritmy at A= 1 se nazývají kologaritmy a používají se ve výpočtech, když se musíme zabývat produkty a podíly. Kolaritmus čísla n rovná se logaritmu reciprokého čísla; těch. kolínská n= log1/ n= – log n. Pokud log2 = 0,3010, pak colog2 = – 0,3010 = 0,6990 – 1. Výhodou použití kologaritmů je, že při výpočtu hodnoty logaritmu výrazů jako pq/r trojitý součet kladných desetinných míst log p+ log q+ kol r je snazší najít než smíšený protokol součtů a rozdílů p+ log q–log r.

Příběh.

Princip, který je základem jakéhokoli systému logaritmů, je znám již velmi dlouho a lze jej vysledovat až do starověké babylonské matematiky (kolem roku 2000 př. n. l.). V té době se k výpočtu složeného úroku používala interpolace mezi tabulkovými hodnotami kladných celočíselných mocnin celých čísel. Mnohem později Archimedes (287–212 př. n. l.) použil mocniny 108 k nalezení horní hranice počtu zrnek písku potřebných k úplnému vyplnění tehdy známého vesmíru. Archimédes upozornil na vlastnost exponentů, která je základem účinnosti logaritmů: součin mocnin odpovídá součtu exponentů. Na konci středověku a na počátku novověku se matematici stále více začali obracet ke vztahu mezi geometrickými a aritmetickými posloupnostmi. M. Stiefel ve své eseji Celočíselná aritmetika(1544) dal tabulku kladných a záporných mocnin čísla 2:

Stiefel si všiml, že součet dvou čísel v prvním řádku (řada s exponentem) se rovná exponentu dvou odpovídajících součinu dvou odpovídajících čísel ve spodním řádku (řada s exponentem). V souvislosti s touto tabulkou Stiefel formuloval čtyři pravidla ekvivalentní čtyřem moderním pravidlům pro operace s exponenty nebo čtyřem pravidlům pro operace s logaritmy: součet na horním řádku odpovídá součinu na spodním řádku; odečítání na horním řádku odpovídá dělení na spodním řádku; násobení na horním řádku odpovídá umocnění na spodním řádku; dělení na horním řádku odpovídá zakořenění na spodním řádku.

Pravidla podobná Stiefelovým pravidlům vedla J. Napera k formálnímu zavedení prvního systému logaritmů ve své práci. Popis úžasné tabulky logaritmů, publikované v roce 1614. Ale Napierovy myšlenky se zabývaly problémem převodu produktů na sumy od té doby, více než deset let před zveřejněním své práce, Napier obdržel z Dánska zprávu, že na observatoři Tycho Brahe jeho asistenti měli metodu, která je možné převádět produkty na součty. Metoda diskutovaná ve zprávě, kterou Napier obdržel, byla založena na použití trigonometrických vzorců jako

proto Naperovy tabulky sestávaly hlavně z logaritmů goniometrických funkcí. Přestože pojem báze nebyl explicitně zahrnut do definice navržené Napierem, roli ekvivalentní bázi systému logaritmů v jeho systému hrálo číslo (1 – 10 –7)ґ10 7, přibližně rovné 1/ E.

Nezávisle na Naperovi a téměř současně s ním vynalezl a vydal v roce 1620 J. Bürgi v Praze typově velmi podobný systém logaritmů. Aritmetické a geometrické postupové tabulky. Jednalo se o tabulky antilogaritmů k základně (1 + 10 –4) ґ10 4, poměrně dobrá aproximace počtu E.

V systému Naper byl logaritmus čísla 107 považován za nulu, a jak čísla klesala, logaritmy se zvyšovaly. Když G. Briggs (1561–1631) navštívil Napier, oba se shodli, že by bylo výhodnější použít jako základ číslo 10 a považovat logaritmus jedné za nulu. Potom, jak se čísla zvyšovala, jejich logaritmy se zvětšovaly. Tak jsme získali moderní systém dekadických logaritmů, jehož tabulku publikoval Briggs ve své práci Logaritmická aritmetika(1620). Logaritmy k základně E, i když ne přesně ty, které představil Naper, jsou často nazývány Naperovými. Termíny „charakteristika“ a „mantisa“ navrhl Briggs.

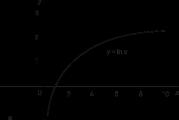
První logaritmy používaly z historických důvodů aproximace k číslům 1/ E A E. O něco později se myšlenka přirozených logaritmů začala spojovat se studiem oblastí pod hyperbolou xy= 1 (obr. 1). V 17. stol bylo ukázáno, že oblast ohraničená touto křivkou, osou X a ordináty X= 1 a X = A(na obr. 1 je tato oblast pokryta výraznějšími a řídkými tečkami) zvyšuje aritmetický postup, když A roste exponenciálně. Právě tato závislost vzniká v pravidlech pro operace s exponenty a logaritmy. To vedlo k tomu, že se Naperovské logaritmy nazývaly „hyperbolické logaritmy“.

Logaritmická funkce.

Bývaly doby, kdy byly logaritmy považovány pouze za výpočetní prostředek, ale v 18. století se především díky Eulerově práci zformoval koncept logaritmické funkce. Graf takové funkce y= log X, jehož pořadnice se zvětšují v aritmetické progresi, zatímco úsečky rostou v geometrické progresi, je uveden na Obr. 2, A. Graf inverzní nebo exponenciální funkce y = e x, jehož ordináty se zvyšují v geometrické progresi a jejichž úsečky se zvyšují v aritmetické progresi, je znázorněno na Obr. 2, b. (Křivky y=log X A y = 10X tvarově podobný křivkám y= log X A y = e x.) Byly také navrženy alternativní definice logaritmické funkce, např.

kpi; a podobně přirozené logaritmy čísla -1 jsou komplexní čísla tvaru (2 k + 1)pí, Kde k– celé číslo. Podobná tvrzení platí pro obecné logaritmy nebo jiné systémy logaritmů. Navíc lze definici logaritmů zobecnit pomocí Eulerových identit tak, aby zahrnovaly komplexní logaritmy komplexních čísel.

Alternativní definici logaritmické funkce poskytuje funkční analýza. Li F(X) – spojitá funkce reálného čísla X, který má následující tři vlastnosti: F (1) = 0, F (b) = 1, F (uv) = F (u) + F (proti), Že F(X) je definován jako logaritmus čísla X na základě b. Tato definice má oproti definici uvedené na začátku tohoto článku řadu výhod.

Aplikace.

Logaritmy byly původně používány pouze pro zjednodušení výpočtů a tato aplikace je stále jednou z jejich nejdůležitějších. Výpočet součinů, kvocientů, mocnin a odmocnin usnadňuje nejen široká dostupnost publikovaných logaritmických tabulek, ale také použití tzv. logaritmické pravítko - výpočetní nástroj, jehož princip fungování je založen na vlastnostech logaritmů. Pravítko je vybaveno logaritmickými stupnicemi, tzn. vzdálenost od čísla 1 k libovolnému číslu X zvoleno tak, aby se rovnalo log X; Posouváním jedné stupnice vůči druhé je možné vykreslit součty nebo rozdíly logaritmů, což umožňuje číst přímo ze stupnice součiny nebo podíly odpovídajících čísel. Můžete také využít výhod reprezentace čísel v logaritmické formě. logaritmický papír pro vykreslování grafů (papír s logaritmickými stupnicemi natištěnými na obou souřadnicových osách). Pokud funkce splňuje mocninný zákon tvaru y = kxn, pak jeho logaritmický graf vypadá jako přímka, protože log y=log k + n log X– rovnice lineární vzhledem k log y a log X. Naopak, pokud logaritmický graf nějaké funkční závislosti vypadá jako přímka, pak je tato závislost mocninná. Semi-log papír (kde osa y má logaritmické měřítko a osa x má jednotné měřítko) je užitečný, když potřebujete identifikovat exponenciální funkce. Rovnice formuláře y = kb rx vyskytují se vždy, když se množství, jako je populace, množství radioaktivního materiálu nebo bankovní zůstatek, snižuje nebo zvyšuje tempem úměrným množství populace, radioaktivního materiálu nebo peněz, které jsou aktuálně k dispozici. Pokud je taková závislost vynesena na semilogaritmický papír, bude graf vypadat jako přímka.

Logaritmická funkce vzniká ve spojení s širokou škálou přírodních forem. Květy v květenstvích slunečnice jsou uspořádány v logaritmických spirálách, lastury měkkýšů jsou zkroucené Nautilus, rohy horských ovcí a papouščí zobáky. Všechny tyto přirozené tvary mohou sloužit jako příklady křivky známé jako logaritmická spirála, protože v polárním souřadnicovém systému je její rovnice r = ae bq, nebo ln r= log A + bq. Taková křivka je popsána pohyblivým bodem, jehož vzdálenost od pólu se geometrickou progresí zvětšuje a úhel popsaný jejím poloměrovým vektorem se zvětšuje v aritmetickém postupu. Všudypřítomnost takové křivky, a tedy i logaritmické funkce, dobře ilustruje skutečnost, že se vyskytuje v tak vzdálených a zcela odlišných oblastech, jako je obrys excentrické vačky a trajektorie nějakého hmyzu letícího ke světlu.

Takže máme mocniny dvou. Pokud vezmete číslo ze spodního řádku, můžete snadno najít moc, na kterou budete muset zvýšit dvojku, abyste toto číslo získali. Chcete-li například získat 16, musíte zvýšit dvě na čtvrtou mocninu. A abyste získali 64, musíte zvýšit dvě na šestou mocninu. To je vidět z tabulky.

A teď vlastně definice logaritmu:

Základ a logaritmus x je mocnina, na kterou musí být a zvýšeno, abychom dostali x.

Zápis: log a x = b, kde a je základ, x je argument, b je to, čemu se ve skutečnosti rovná logaritmus.

Například 2 3 = 8 ⇒ log 2 8 = 3 (základ 2 logaritmu 8 je tři, protože 2 3 = 8). Se stejným úspěchem log 2 64 = 6, protože 2 6 = 64.

Operace nalezení logaritmu čísla k danému základu se nazývá logaritmizace. Přidejme tedy do naší tabulky nový řádek:

2 1	2 2	2 3	2 4	2 5	2 6
2	4	8	16	32	64
log 2 2 = 1	log 2 4 = 2	log 2 8 = 3	log 2 16 = 4	log 2 32 = 5	log 2 64 = 6

Bohužel ne všechny logaritmy lze vypočítat tak snadno. Zkuste například najít log 2 5. Číslo 5 není v tabulce, ale logika velí, že logaritmus bude ležet někde na intervalu. Protože 22< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.

Taková čísla se nazývají iracionální: čísla za desetinnou čárkou lze psát do nekonečna a nikdy se neopakují. Pokud se logaritmus ukáže jako iracionální, je lepší jej nechat tak: log 2 5, log 3 8, log 5 100.

Je důležité pochopit, že logaritmus je výraz se dvěma proměnnými (základ a argument). Mnoho lidí si nejprve pletou, kde je základ a kde argument. Abyste předešli nepříjemným nedorozuměním, podívejte se na obrázek:

[Popis k obrázku]

Před námi není nic jiného než definice logaritmu. Pamatovat si: logaritmus je síla, do kterého je nutné zabudovat základnu pro získání argumentu. Je to základna, která je zvednutá na mocninu - na obrázku je zvýrazněna červeně. Ukazuje se, že základna je vždy na dně! Hned na první hodině říkám svým studentům toto úžasné pravidlo – a nevznikají žádné zmatky.

Definici jsme vymysleli – zbývá jen naučit se počítat logaritmy, tzn. zbavit se znaku "log". Pro začátek si všimneme, že z definice plynou dvě důležité skutečnosti:

1. Argument a základ musí být vždy větší než nula. Vyplývá to z definice stupně racionálním exponentem, na který je redukována definice logaritmu.
2. Základ musí být odlišný od jednoho, protože jeden do jakéhokoli stupně stále zůstává jedním. Z tohoto důvodu je otázka „k jaké síle musí být člověk povýšen, aby získal dva“ smysl. Takový stupeň neexistuje!

Taková omezení se nazývají rozsah přijatelných hodnot(ODZ). Ukazuje se, že ODZ logaritmu vypadá takto: log a x = b ⇒ x > 0, a > 0, a ≠ 1.

Všimněte si, že pro číslo b (hodnota logaritmu) neexistují žádná omezení. Logaritmus může být například záporný: log 2 0,5 = −1, protože 0,5 = 2 −1.

Nyní však uvažujeme pouze o číselných výrazech, kde není vyžadováno znát VA logaritmu. Všechna omezení již autoři úkolů zohlednili. Ale když do hry vstoupí logaritmické rovnice a nerovnosti, stanou se požadavky DL povinnými. Ostatně základ a argument může obsahovat velmi silné konstrukce, které nemusí nutně odpovídat výše uvedeným omezením.

Nyní se podívejme na obecné schéma pro výpočet logaritmů. Skládá se ze tří kroků:

1. Vyjádřete základ a a argument x jako mocninu s minimálním možným základem větším než jedna. Po cestě je lepší se zbavit desetinných míst;
2. Řešte rovnici pro proměnnou b: x = a b ;
3. Výsledné číslo b bude odpovědí.

To je vše! Pokud se logaritmus ukáže jako iracionální, bude to vidět již v prvním kroku. Požadavek, aby byl základ větší než jedna, je velmi důležitý: snižuje se tím pravděpodobnost chyby a výrazně se zjednodušují výpočty. Je to stejné jako s desetinnými zlomky: pokud je okamžitě převedete na obyčejné, bude mnohem méně chyb.

Podívejme se, jak toto schéma funguje na konkrétních příkladech:

Úkol. Vypočítejte logaritmus: log 5 25

1. Představme si základ a argument jako mocninu pěti: 5 = 5 1 ; 25 = 52;
2. Vytvořme a vyřešme rovnici:
   log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2;
3. Dostali jsme odpověď: 2.

Úkol. Vypočítejte logaritmus:

[Popis k obrázku]

Úkol. Vypočítejte logaritmus: log 4 64

1. Představme si základ a argument jako mocninu dvou: 4 = 2 2 ; 64 = 26;
2. Vytvořme a vyřešme rovnici:
   log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3;
3. Dostali jsme odpověď: 3.

Úkol. Vypočítejte logaritmus: log 16 1

1. Představme si základ a argument jako mocninu dvou: 16 = 2 4 ; 1 = 20;
2. Vytvořme a vyřešme rovnici:
   log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0;
3. Dostali jsme odpověď: 0.

Úkol. Vypočítejte logaritmus: log 7 14

1. Představme si základ a argument jako mocninu sedmi: 7 = 7 1 ; 14 nelze reprezentovat jako mocninu sedmi, protože 7 1< 14 < 7 2 ;
2. Z předchozího odstavce vyplývá, že logaritmus se nepočítá;
3. Odpověď je žádná změna: log 7 14.

Malá poznámka k poslednímu příkladu. Jak si můžete být jisti, že číslo není přesnou mocninou jiného čísla? Je to velmi jednoduché – stačí to započítat do hlavních faktorů. A pokud takové faktory nelze shrnout do mocnin se stejnými exponenty, pak původní číslo není přesná mocnina.

Úkol. Zjistěte, zda jsou čísla přesné mocniny: 8; 48; 81; 35; 14.

8 = 2 · 2 · 2 = 2 3 - přesný stupeň, protože existuje pouze jeden násobitel;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 - není přesná mocnina, protože existují dva faktory: 3 a 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 - přesný stupeň;
35 = 7 · 5 - opět není přesná mocnina;
14 = 7 · 2 - opět není přesný stupeň;

Všimněte si také, že prvočísla sama o sobě jsou vždy přesné mocniny samých sebe.

Desetinný logaritmus

Některé logaritmy jsou tak běžné, že mají speciální název a symbol.

Desetinný logaritmus x je logaritmus se základem 10, tj. Mocnina, na kterou musí být umocněno číslo 10, aby získalo číslo x. Označení: lg x.

Například log 10 = 1; Ig100 = 2; lg 1000 = 3 - atd.

Až se od této chvíle v učebnici objeví fráze jako „Najít lg 0,01“, vězte, že se nejedná o překlep. Toto je dekadický logaritmus. Pokud však tento zápis neznáte, můžete jej vždy přepsat:
log x = log 10 x

Vše, co platí pro běžné logaritmy, platí také pro dekadické logaritmy.

Přirozený logaritmus

Existuje další logaritmus, který má své vlastní označení. V některých ohledech je dokonce důležitější než desítkové. Mluvíme o přirozeném logaritmu.

Přirozený logaritmus x je logaritmus se základem e, tj. mocnina, na kterou musí být číslo e zvýšeno, abychom získali číslo x. Označení: ln x .

Mnozí se budou ptát: jaké je číslo e? Toto je iracionální číslo, jeho přesnou hodnotu nelze najít a zapsat. Uvedu pouze první čísla:
e = 2,718281828459...

Nebudeme se podrobně zabývat tím, co toto číslo je a proč je potřeba. Pamatujte, že e je základem přirozeného logaritmu:
ln x = log e x

Tedy ln e = 1; lne2 = 2; ln e 16 = 16 - atd. Na druhou stranu, ln 2 je iracionální číslo. Obecně platí, že přirozený logaritmus jakéhokoli racionálního čísla je iracionální. Samozřejmě kromě jednoho: ln 1 = 0.

Pro přirozené logaritmy platí všechna pravidla, která platí pro běžné logaritmy.

Zachování vašeho soukromí je pro nás důležité. Z tohoto důvodu jsme vyvinuli Zásady ochrany osobních údajů, které popisují, jak používáme a uchováváme vaše informace. Přečtěte si prosím naše zásady ochrany osobních údajů a dejte nám vědět, pokud máte nějaké dotazy.

Shromažďování a používání osobních údajů

Osobní údaje jsou údaje, které lze použít k identifikaci nebo kontaktování konkrétní osoby.

Kdykoli nás budete kontaktovat, můžete být požádáni o poskytnutí svých osobních údajů.

Níže jsou uvedeny některé příklady typů osobních údajů, které můžeme shromažďovat, a jak takové informace můžeme používat.

Jaké osobní údaje shromažďujeme:

• Když odešlete žádost na webu, můžeme shromažďovat různé informace, včetně vašeho jména, telefonního čísla, e-mailové adresy atd.

Jak používáme vaše osobní údaje:

• Osobní údaje, které shromažďujeme, nám umožňují kontaktovat vás s jedinečnými nabídkami, akcemi a dalšími událostmi a nadcházejícími událostmi.
• Čas od času můžeme použít vaše osobní údaje k zasílání důležitých oznámení a sdělení.
• Osobní údaje můžeme také používat pro interní účely, jako je provádění auditů, analýzy dat a různé výzkumy, abychom zlepšili služby, které poskytujeme, a abychom vám poskytli doporučení týkající se našich služeb.
• Pokud se účastníte slosování o ceny, soutěže nebo podobné propagační akce, můžeme použít vámi poskytnuté informace ke správě takových programů.

Zpřístupnění informací třetím stranám

Informace, které od vás obdržíme, nesdělujeme třetím stranám.

Výjimky:

• V případě potřeby – v souladu se zákonem, soudním postupem, v soudním řízení a/nebo na základě veřejných žádostí nebo žádostí vládních orgánů v Ruské federaci – zveřejnit vaše osobní údaje. Můžeme také zveřejnit informace o vás, pokud usoudíme, že takové zveřejnění je nezbytné nebo vhodné pro účely bezpečnosti, vymáhání práva nebo jiné veřejné důležité účely.
• V případě reorganizace, fúze nebo prodeje můžeme osobní údaje, které shromažďujeme, předat příslušné nástupnické třetí straně.

Ochrana osobních údajů

Přijímáme opatření – včetně administrativních, technických a fyzických – k ochraně vašich osobních údajů před ztrátou, krádeží a zneužitím, stejně jako neoprávněným přístupem, zveřejněním, pozměněním a zničením.

Respektování vašeho soukromí na úrovni společnosti

Abychom zajistili, že jsou vaše osobní údaje v bezpečí, sdělujeme našim zaměstnancům standardy ochrany soukromí a zabezpečení a přísně prosazujeme postupy ochrany osobních údajů.

\(a^(b)=c\) \(\Šipka doleva\) \(\log_(a)(c)=b\)

Pojďme si to vysvětlit jednodušeji. Například \(\log_(2)(8)\) se rovná mocnině, na kterou musí být umocněno \(2\), aby bylo dosaženo \(8\). Z toho je zřejmé, že \(\log_(2)(8)=3\).

Příklady:		\(\log_(5)(25)=2\)		protože \(5^(2)=25\)
		\(\log_(3)(81)=4\)		protože \(3^(4)=81\)
		\(\log_(2)\)\(\frac(1)(32)\) \(=-5\)		protože \(2^(-5)=\)\(\frac(1)(32)\)

Argument a základ logaritmu

Každý logaritmus má následující „anatomii“:

Argument logaritmu se obvykle zapisuje na jeho úrovni a základna se zapisuje v dolním indexu blíže znaménku logaritmu. A tento záznam zní takto: „logaritmus z dvaceti pěti na základ pět“.

Jak vypočítat logaritmus?

Chcete-li vypočítat logaritmus, musíte odpovědět na otázku: na jakou mocninu by se měla základna zvýšit, abyste získali argument?

Například, vypočítejte logaritmus: a) \(\log_(4)(16)\) b) \(\log_(3)\)\(\frac(1)(3)\) c) \(\log_(\ sqrt (5))(1)\) d) \(\log_(\sqrt(7))(\sqrt(7))\) e) \(\log_(3)(\sqrt(3))\)

a) Na jakou mocninu se musí zvýšit \(4\), aby dostal \(16\)? Pochopitelně ten druhý. Proto:

\(\log_(4)(16)=2\)

\(\log_(3)\)\(\frac(1)(3)\) \(=-1\)

c) Na jakou mocninu se musí zvýšit \(\sqrt(5)\), aby se dostalo \(1\)? Jaká síla dělá nějakou jedničku? Nula, samozřejmě!

\(\log_(\sqrt(5))(1)=0\)

d) Na jakou mocninu musí být \(\sqrt(7)\) zvýšeno, aby bylo dosaženo \(\sqrt(7)\)? Za prvé, jakékoli číslo s první mocninou se rovná samo sobě.

\(\log_(\sqrt(7))(\sqrt(7))=1\)

e) Na jakou mocninu je třeba zvýšit \(3\), aby se získal \(\sqrt(3)\)? Z toho víme, že se jedná o zlomkovou mocninu, což znamená, že druhá odmocnina je mocninou \(\frac(1)(2)\) .

\(\log_(3)(\sqrt(3))=\)\(\frac(1)(2)\)

Příklad : Vypočítat logaritmus \(\log_(4\sqrt(2))(8)\)

Řešení :

\(\log_(4\sqrt(2))(8)=x\)		Musíme najít hodnotu logaritmu, označme ji jako x. Nyní použijeme definici logaritmu: \(\log_(a)(c)=b\) \(\Šipka doleva\) \(a^(b)=c\)
\((4\sqrt(2))^(x)=8\)		Co spojuje \(4\sqrt(2)\) a \(8\)? Dvě, protože obě čísla mohou být reprezentována dvojkami: \(4=2^(2)\) \(\sqrt(2)=2^(\frac(1)(2))\) \(8=2^(3)\)
\(((2^(2)\cdot2^(\frac(1)(2))))^(x)=2^(3)\)		Vlevo používáme vlastnosti stupně: \(a^(m)\cdot a^(n)=a^(m+n)\) a \((a^(m))^(n)= a^(m\cdot n)\)
\(2^(\frac(5)(2)x)=2^(3)\)		Základy se rovnají, přecházíme k rovnosti ukazatelů
\(\frac(5x)(2)\) \(=3\)		Vynásobte obě strany rovnice \(\frac(2)(5)\)
		Výsledná odmocnina je hodnota logaritmu

Odpovědět : \(\log_(4\sqrt(2))(8)=1,2\)

Proč byl logaritmus vynalezen?

Abychom to pochopili, vyřešme rovnici: \(3^(x)=9\). Stačí přiřadit \(x\), aby rovnice fungovala. Samozřejmě, \(x=2\).

Nyní vyřešte rovnici: \(3^(x)=8\).Čemu se x rovná? O to tu jde.

Ti nejchytřejší řeknou: "X je o něco méně než dva." Jak přesně napsat toto číslo? K zodpovězení této otázky byl vynalezen logaritmus. Díky němu zde může být odpověď zapsána jako \(x=\log_(3)(8)\).

Chci zdůraznit, že \(\log_(3)(8)\), jako každý logaritmus je jen číslo. Ano, vypadá to nezvykle, ale je to krátké. Protože pokud bychom to chtěli zapsat jako desetinné, vypadalo by to takto: \(1.892789260714.....\)

Příklad : Vyřešte rovnici \(4^(5x-4)=10\)

Řešení :

\(4^(5x-4)=10\)		\(4^(5x-4)\) a \(10\) nelze přenést na stejnou základnu. To znamená, že se bez logaritmu neobejdete. Použijme definici logaritmu: \(a^(b)=c\) \(\Šipka doleva\) \(\log_(a)(c)=b\)
\(\log_(4)(10)=5x-4\)		Otočme rovnici tak, aby X bylo vlevo
\(5x-4=\log_(4)(10)\)		Před námi. Přesuneme \(4\) doprava. A nebojte se logaritmu, zacházejte s ním jako s obyčejným číslem.
\(5x=\log_(4)(10)+4\)		Vydělte rovnici 5
\(x=\)\(\frac(\log_(4)(10)+4)(5)\)		Toto je náš kořen. Ano, vypadá to nezvykle, ale nevybírají si odpověď.

Odpovědět : \(\frac(\log_(4)(10)+4)(5)\)

Desetinné a přirozené logaritmy

Jak je uvedeno v definici logaritmu, jeho základem může být jakékoli kladné číslo kromě jedné \((a>0, a\neq1)\). A mezi všemi možnými bázemi jsou dva, které se vyskytují tak často, že pro logaritmy s nimi byl vynalezen speciální krátký zápis:

Přirozený logaritmus: logaritmus, jehož základem je Eulerovo číslo \(e\) (rovné přibližně \(2,7182818…\)) a logaritmus je zapsán jako \(\ln(a)\).

to znamená, \(\ln(a)\) je totéž jako \(\log_(e)(a)\)

Desetinný logaritmus: Logaritmus, jehož základ je 10, se zapisuje \(\lg(a)\).

to znamená, \(\lg(a)\) je totéž jako \(\log_(10)(a)\), kde \(a\) je nějaké číslo.

Základní logaritmická identita

Logaritmy mají mnoho vlastností. Jedna z nich se nazývá „Základní logaritmická identita“ a vypadá takto:

\(a^(\log_(a)(c))=c\)

Tato vlastnost vyplývá přímo z definice. Podívejme se, jak přesně tento vzorec vznikl.

Připomeňme si krátký zápis definice logaritmu:

jestliže \(a^(b)=c\), pak \(\log_(a)(c)=b\)

To znamená, že \(b\) je totéž jako \(\log_(a)(c)\). Potom můžeme do vzorce \(a^(b)=c\) místo \(b\) napsat \(\log_(a)(c)\). Ukázalo se, že \(a^(\log_(a)(c))=c\) - hlavní logaritmická identita.

Můžete najít další vlastnosti logaritmů. S jejich pomocí můžete zjednodušit a vypočítat hodnoty výrazů s logaritmy, které je obtížné vypočítat přímo.

Příklad : Najděte hodnotu výrazu \(36^(\log_(6)(5))\)

Řešení :

Odpovědět : \(25\)

Jak zapsat číslo jako logaritmus?

Jak bylo uvedeno výše, každý logaritmus je pouze číslo. Platí to i naopak: libovolné číslo lze zapsat jako logaritmus. Například víme, že \(\log_(2)(4)\) se rovná dvěma. Pak místo dvou můžete napsat \(\log_(2)(4)\).

Ale \(\log_(3)(9)\) se také rovná \(2\), což znamená, že můžeme také psát \(2=\log_(3)(9)\) . Podobně s \(\log_(5)(25)\) as \(\log_(9)(81)\) atd. To znamená, že se ukazuje

\(2=\log_(2)(4)=\log_(3)(9)=\log_(4)(16)=\log_(5)(25)=\log_(6)(36)=\ log_(7)(49)...\)

Pokud tedy potřebujeme, můžeme napsat dvojku jako logaritmus s libovolným základem kdekoli (ať už v rovnici, ve výrazu nebo v nerovnosti) - jednoduše zapíšeme základ na druhou jako argument.

S trojkou je to stejné – lze ji zapsat jako \(\log_(2)(8)\), nebo jako \(\log_(3)(27)\), nebo jako \(\log_(4)( 64) \)... Zde zapíšeme základ v krychli jako argument:

\(3=\log_(2)(8)=\log_(3)(27)=\log_(4)(64)=\log_(5)(125)=\log_(6)(216)=\ log_(7)(343)...\)

A se čtyřmi:

\(4=\log_(2)(16)=\log_(3)(81)=\log_(4)(256)=\log_(5)(625)=\log_(6)(1296)=\ log_(7)(2401)...\)

A s mínus jedna:

\(-1=\) \(\log_(2)\)\(\frac(1)(2)\) \(=\) \(\log_(3)\)\(\frac(1)( 3)\) \(=\) \(\log_(4)\)\(\frac(1)(4)\) \(=\) \(\log_(5)\)\(\frac(1) )(5)\) \(=\) \(\log_(6)\)\(\frac(1)(6)\) \(=\) \(\log_(7)\)\(\frac (1) (7)\) \(...\)

A s jednou třetinou:

\(\frac(1)(3)\) \(=\log_(2)(\sqrt(2))=\log_(3)(\sqrt(3))=\log_(4)(\sqrt( 4))=\log_(5)(\sqrt(5))=\log_(6)(\sqrt(6))=\log_(7)(\sqrt(7))...\)

Jakékoli číslo \(a\) může být reprezentováno jako logaritmus se základem \(b\): \(a=\log_(b)(b^(a))\)

Příklad : Najděte význam výrazu \(\frac(\log_(2)(14))(1+\log_(2)(7))\)

Řešení :

Odpovědět : \(1\)

Co je to logaritmus?

Pozornost!
Existují další
materiály ve zvláštní sekci 555.
Pro ty, kteří jsou velmi "ne moc..."
A pro ty, kteří „moc…“)

Co je to logaritmus? Jak řešit logaritmy? Tyto otázky mnohé absolventy matou. Tradičně je téma logaritmů považováno za složité, nepochopitelné a děsivé. Zejména rovnice s logaritmy.

To absolutně není pravda. Absolutně! nevěříš mi? Pokuta. Nyní za pouhých 10–20 minut:

1. Pochopíte co je logaritmus.

2. Naučte se řešit celou třídu exponenciálních rovnic. I když jste o nich nic neslyšeli.

3. Naučte se počítat jednoduché logaritmy.

Navíc k tomu budete potřebovat pouze znát násobilku a jak zvýšit číslo na mocninu...

Mám pocit, že máš pochybnosti... Dobře, dobře, označ si čas! Jít!

Nejprve si v hlavě vyřešte tuto rovnici:

Pokud se vám tato stránka líbí...

Mimochodem, mám pro vás několik dalších zajímavých stránek.)

Můžete si procvičit řešení příkladů a zjistit svou úroveň. Testování s okamžitým ověřením. Pojďme se učit - se zájmem!)

Můžete se seznámit s funkcemi a derivacemi.