1. Axiális szakasz A henger a hengernek a tengelyén átmenő sík által alkotott szakasza. A henger tengelyirányú keresztmetszete az téglalap.

2. Henger metszete, amelynek síkja párhuzamos az alappal.
Ebben az esetben a keresztmetszet az alappal egyenlő és azzal párhuzamos kör.

Kúp

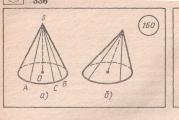
A kúp egy geometriai test, amely egy körből áll, okokból kúp, egy pont, amely nem a kör síkjában fekszik, − csúcsok kúp és minden szegmens, amely a kúp tetejét az alap pontjaival összeköti.

A kúp csúcsát az alapkör pontjaival összekötő szakaszokat ún alakítás kúp

A kúpot hívják közvetlen, ha a kúp tetejét az alap középpontjával összekötő egyenes merőleges az alap síkjára.

Tovább rizs. A) egyenes kúp, b) ferde kúp.

A következőkben csak egy egyenes kúpot veszünk figyelembe!

S- a kúp teteje.

Kör középpontokkal RÓL RŐL– a kúp alapja.

S.A.,C.B., SC– kúpok kialakítása.

Magasság A kúp csúcsától az alap síkjához ereszkedő merőlegesnek nevezzük.

Tengely egy kúp egy egyenes, amely tartalmazza a magasságát ( ÍGY).

A kúp tulajdonságai:

A kúp generátorai egyenlőek.

A kúpot egy derékszögű háromszög oldala körüli elforgatásával nyert testnek tekinthetjük.

A kúp legegyszerűbb szakaszai.

1. Axiális szakasz A kúp a kúpnak a tengelyén áthaladó sík metszete. A kúp tengelyirányú szakasza az háromszög.

2. Az alappal párhuzamos síkú kúp metszete.
Ebben az esetben a keresztmetszet az alaphoz hasonló és azzal párhuzamos kör.

A labda egy geometriai test, amely a tér összes olyan pontjából áll, amelyek távolsága nem nagyobb, mint egy adott ponttól.

Ez a pont ( RÓL RŐL) nak, nek hívják központ labda, és ez a távolság az sugár labda.

A labda határát ún gömb alakú felület vagy gömb.

Minden olyan szakaszt, amely a golyó középpontját a gömbfelület egy pontjával összeköti, nevezzük sugár labda ( O.D., OB, OA).

Golyó átmérője egy gömbfelület két pontját összekötő szakasz, amely áthalad a labda középpontján ( AB).

A labda tulajdonságai:

A labda sugarai egyenlőek;

A golyó átmérője egyenlő.

A labdát egy félkör átmérője körüli elforgatásával nyert testnek tekinthetjük.

A labda legegyszerűbb szakaszai

1. Egy golyó metszete a középpontján áthaladó síkkal. Ebben az esetben a szakasz az nagy kör.

2. Egy labda metszete síkkal Nemáthalad a középpontján. Ebben az esetben a szakasz az kör.

Hengeres felület m Egy görbe mentén mozgó m egyenes egy hengeres felületet ír le. Ha ez a görbe zárt, akkor zárt hengeres felületet írunk le. Ha egy zárt görbe kör alakú, akkor körhengert írunk le. Ha az m egyenes merőleges a görbe síkjára, akkor egy jobb oldali körhengert írunk le HENGERTÍPUSOK Elliptikus henger HENGERTÍPUSOK Hiperbolikus henger HENGERTÍPUSOK Parabolahenger 2014. 07. 26. Definition of a6cylinder. A henger olyan test, amely két, nem ugyanabban a síkban elhelyezkedő körből áll, amelyeket párhuzamos eltolással kombinálnak, valamint e körök megfelelő pontjait összekötő összes szegmensből. Henger Egy hengert úgy kaphatunk, hogy egy téglalapot egy olyan egyenes körül forgatunk, amely a henger bármely oldalát tartalmazza. A henger sugara az alapjának sugara. A henger magassága az alapjainak síkjai közötti távolság. A henger tengelye egy egyenes, amely az alapok középpontjain halad át. A henger tulajdonságai. 1) Az alapok egyenlőek és párhuzamosak. 2) A henger összes generatricája párhuzamos és egyenlő egymással A henger kidolgozása A henger oldalfelülete téglalappá van kialakítva, melynek egyik oldala a henger magassága, másik oldala az alap kerületének hossza. Az egyenlő oldalú henger olyan henger, amelynek tengelymetszete a henger négyzetes metszete. A tengelyével párhuzamos síkú henger keresztmetszete téglalap. Két oldala a henger generatricája, a másik kettő pedig az alapok párhuzamos húrjai. A hengernek a henger tengelyén áthaladó szakaszát axiális szakasznak nevezzük, és egyben téglalap is. A henger alapjának síkjával párhuzamos sík metszi a henger oldalfelületét az alap kerületével megegyező kör mentén. Érintősík Ha egy síknak közös egyenese van az oldalfelülettel, akkor ezt a síkot érintősíknak nevezzük. Az érintési vonal a henger generatrixa A henger teljes és oldalfelülete A henger oldalfelülete egy téglalap, melynek egyik oldala a henger magassága, a másik a kerülete. A henger teljes felülete két körből és egy oldalfelületből áll. L H 2 RH S a henger oldalfelülete és S a kör R 2 R 2 RH 2 R (R H) 2 S a kör S oldala S a 2. henger teljes felülete és a 2. henger felülete és A henger térfogata A a henger egyenlő az alapterület és a henger magasságának szorzatával. V S alap V R 2 H H Magyarázza el, mi az a jobb oldali körhenger? Mekkora a henger sugara, magassága, generatrixa és tengelye? Mekkora a henger tengelyirányú metszete? Melyik hengert nevezzük egyenlő oldalúnak? Mekkora a hengernek a henger tengelyére merőleges sík metszete? Mit értünk a henger oldalsó és teljes felületén? Hogyan találjuk meg a henger oldalsó és teljes felületét? A HENGER ELEMEI 1. feladat. A henger tengelyirányú metszete egy négyzet, melynek területe Q. Határozza meg a henger alapterületét! Adott: henger, tengelymetszete - négyzet Smetszet = Q Keresse: Sbas = Kör Megoldás: 2. feladat. A henger oldalfelülete 4 cm2 területű négyzetté változik. Határozza meg a henger teljes felületét és térfogatát! Tegyük fel, hogy 3 N lkör Adott: henger négyzet = 4 cm2 Keresse: Sp.p., Vcyl. Megoldás: Laboratóriumi és gyakorlati munka Témakör: Henger 1. Definíció, tulajdonságok. 2. Rajz, méretek mm-ben. 3. Számítsa ki: a) alapterületét b) a henger oldalfelületét! c) a henger teljes felülete. d) a henger térfogata. Feladatok A tengelymetszet átlója 48 cm. A henger átlója és generatrixa közötti szög 60o. Keresse meg 1) a henger magasságát; 2) a henger sugara; 3) Sbas A henger magassága 8 cm, sugara 5 cm. Határozza meg a tengelyével párhuzamos sík keresztmetszeti területét, ha e sík és a henger tengelye közötti távolság 3 cm. A henger oldalfelületének területe S. Határozza meg a tengelyirányú keresztmetszetet. a henger keresztmetszete. A hengert úgy kapjuk meg, hogy az egyik oldala körül forgatunk egy α oldalú négyzetet. Határozza meg a következő területek területét: 1) a henger tengelyirányú metszete; 2) a henger teljes felülete Henger Eredetiség a tervezésben és az építészetben Probléma: Mennyivel nő a GAZ-53 autómotor égésterének térfogata, ha a dugattyú átmérője 10 cm és a dugattyúlöket 9 cm? Megoldás V=пR2H: V=3,14 52 9=706,5 (cm3) Feladat Határozza meg a ZIL130 típusú gépkocsi szervokormány-szivattyúja olajtartályának térfogatát, ha átmérője 126 mm, magassága 140 mm Megoldás V=пR2H! =3,14. 3969.140=174477.24

Henger (egyenes körhenger) egy test, amely két körből (egy henger alapjából) áll, amelyeket párhuzamos transzlációval kombinálnak, és az összes szegmensből, amelyek e körök megfelelő pontjait a párhuzamos fordítás során összekötik. Az alapkörök megfelelő pontjait összekötő szakaszokat a henger generátorainak nevezzük.

Íme egy másik definíció:

Henger- egy test, amelyet egy zárt vezetővel ellátott hengeres felület és két párhuzamos sík határol, amelyek metszi ennek a felületnek a generatricáit.

Hengeres felület- olyan felület, amely egy bizonyos görbe mentén egy egyenes mozgásával jön létre. Az egyenest a hengeres felület generatrixának, az ívelt vonalat pedig a hengeres felület vezetőjének nevezzük.

A henger oldalsó felülete- hengeres felület párhuzamos síkokkal határolt része.

Hengeralapok- a henger oldalfelülete által levágott párhuzamos síkok részei.

1. ábra mini

A hengert ún közvetlen(Cm. 1. ábra), ha generátorai merőlegesek az alapok síkjaira. Ellenkező esetben a hengert ún hajlamos.

Kör alakú henger- egy henger, amelynek alapja körök.

Jobb körhenger (csak egy henger) egy téglalap egyik oldala körüli elforgatásával kapott test. Cm. 1. ábra.

Henger sugara az alapjának sugara.

A henger generátora- hengeres felület generatrixa.

Henger magasság az alapok síkjai közötti távolságnak nevezzük. Henger tengelye az alapok középpontjain áthaladó egyenesnek nevezzük. A hengernek a henger tengelyén átmenő sík metszetét ún axiális szakasz.

A henger tengelye párhuzamos a generatrixával, és a henger szimmetriatengelye.

Egy egyenes henger generatrixán átmenő és az ezen a generatrixon áthúzott tengelymetszetre merőleges síkot ún. a henger érintősíkja. Cm. 2. ábra.

A henger oldalfelületének kialakulása- egy téglalap, amelynek oldalai megegyeznek a henger magasságával és az alap kerületével.

A henger oldalfelülete- az oldalsó felület fejlődési területe. $$S_(oldal)=2\pi\cdot rh$$ , ahol h a henger magassága, és r– az alap sugara.

Egy henger teljes felülete- terület, amely megegyezik a henger két alapja és oldalfelülete területének összegével, azaz. a következő képlettel fejezzük ki: $$S_(full)=2\pi\cdot r^2 + 2\pi\cdot rh = 2\pi\cdot r(r+h)$$ , ahol h a henger magassága, és r– az alap sugara.

Bármely henger térfogata egyenlő az alapterület és a magasság szorzatával: $$V = S\cdot h$$ Egy kerek henger térfogata: $$V=\pi r^2 \cdot h$$ , ahol ( r- alapsugár).

A prizma egy speciális hengertípus (a generátorok párhuzamosak az oldalbordákkal, a vezető egy sokszög, amely az alján fekszik). Másrészt egy tetszőleges henger egy degenerált („kisimított”) prizmának tekinthető, amelynek nagyon sok nagyon keskeny lapja van. A gyakorlatban egy hengert nem lehet megkülönböztetni egy ilyen prizmától. A prizma minden tulajdonsága megmarad a hengerben.

A sztereometria a geometriának egy olyan ága, amelyben a térbeli alakzatokat tanulmányozzák. A tér fő alakjai egy pont, egy egyenes és egy sík. A sztereometriában megjelenik a vonalak relatív elrendezésének új típusa: a vonalak keresztezése. Ez egyike azon kevés jelentős különbségnek a sztereometria és a planimetria között, mivel sok esetben a sztereometriai problémákat különböző síkok figyelembevételével oldják meg, amelyekben a planimetriai törvények teljesülnek.

A minket körülvevő természetben sok olyan tárgy található, amelyek ennek az alaknak a fizikai modelljei. Például sok gépalkatrész henger alakú, vagy ezek valamilyen kombinációja, és a templomok és katedrálisok fenséges, henger alakú oszlopai hangsúlyozzák harmóniájukat és szépségüket.

görög − kylindros. Ősi kifejezés. A mindennapi életben - egy papirusz tekercs, egy henger, egy henger (ige - csavarni, tekercs).

Euklidész esetében egy hengert egy téglalap elforgatásával kapunk. Cavalieriben - a generatrix mozgásával (tetszőleges vezetővel - egy „henger”).

Ennek az esszének az a célja, hogy megvizsgáljon egy geometriai testet - egy hengert.

E cél eléréséhez a következő feladatokat kell mérlegelni:

− adjon definíciókat a hengerre;

− mérlegelje a henger elemeit;

− tanulmányozza a henger tulajdonságait;

− mérlegelje a hengerszelvények típusait;

− levezetni a henger területének képletét;

− levezetni a henger térfogatának képletét;

− problémák megoldása henger segítségével.

1.1. A henger definíciója

Tekintsünk egy l egyenest (görbét, törött vagy kevert), amely valamilyen α síkban fekszik, és egy S egyenest, amely ezt a síkot metszi. Egy adott l egyenes minden pontján keresztül az S egyenessel párhuzamos egyeneseket húzunk; az ezen egyenesek által alkotott α felületet hengeres felületnek nevezzük. Az l vonalat e felület vezetőjének nevezzük, az s 1, s 2, s 3,... vonalak a generátorai.

Ha a vezető eltörik, akkor egy ilyen hengeres felület több lapos csíkból áll, amelyek párhuzamos egyenesek párjai közé vannak zárva, és prizmatikus felületnek nevezik. A vezető szaggatott vonal csúcsain áthaladó generatricákat a prizmaszerű felület éleinek nevezzük, a köztük lévő lapos csíkok a lapjai.

Ha bármilyen hengeres felületet tetszőleges síkkal vágunk, amely nem párhuzamos a generátoraival, akkor egy vonalat kapunk, amely erre a felületre is irányadónak tekinthető. A vezetők közül kiemelkedik az, amelyet úgy kapunk, hogy a felületet a felület generatricáira merőleges síkkal vágjuk. Az ilyen szakaszt normál szakasznak, a megfelelő vezetőt pedig normál vezetőnek nevezzük.

Ha a vezető egy zárt (domború) vonal (szakadt vagy ívelt), akkor a megfelelő felületet zárt (konvex) prizmás vagy hengeres felületnek nevezzük. A legegyszerűbb hengeres felületek normál vezetőhelye egy kör. Boncoljunk fel egy zárt konvex prizmás felületet, amelynek két, egymással párhuzamos, de a generátorokkal nem párhuzamos síkja van.

A szakaszokban konvex sokszögeket kapunk. Most a prizmás felületnek az α és α" síkok közé zárt része és az ezekben a síkokban kialakított két sokszögű lemez egy prizmatestnek nevezett testet - prizmát - határol.

Hengeres test - a hengert a prizmához hasonlóan határozzuk meg:
A henger olyan test, amelyet oldalról zárt (domború) hengeres felület, a végein pedig két lapos, párhuzamos alap határol. A henger mindkét alapja egyenlő, és a henger összes alkotóeleme is egyenlő, azaz. egy hengeres felület generatricáinak szegmensei az alapok síkjai között.

A henger (pontosabban körhenger) olyan geometriai test, amely két, nem egy síkban fekvő körből áll, amelyeket párhuzamos eltolással egyesítenek, és e körök megfelelő pontjait összekötő összes szegmensből (1. ábra). .

A köröket a henger alapjainak, a körök kerületének megfelelő pontjait összekötő szakaszokat pedig a henger generátorainak nevezzük.

Mivel a párhuzamos transzláció mozgás, a henger alapjai egyenlők.

Mivel a párhuzamos transzláció során a sík párhuzamos síkba (vagy önmagába) alakul át, ezért a henger alapjai párhuzamos síkban helyezkednek el.

Mivel párhuzamos transzláció során a pontok párhuzamos (vagy egybeeső) egyenesek mentén azonos távolsággal tolódnak el, ezért a henger generátorai párhuzamosak és egyenlőek.

A henger felülete az alapból és az oldalfelületből áll. Az oldalsó felület generatricákból áll.

Egy hengert egyenesnek nevezünk, ha generátorai merőlegesek az alapok síkjaira.

Egy egyenes henger vizuálisan elképzelhető geometriai testként, amely egy téglalapot ír le, amikor az oldala körül tengelyként forgatjuk (2. ábra).

Rizs. 2 − Egyenes henger

A következőkben csak az egyenes hengert fogjuk figyelembe venni, a rövidség kedvéért egyszerűen hengernek nevezzük.

A henger sugara az alapjának sugara. A henger magassága az alapjainak síkjai közötti távolság. A henger tengelye egy egyenes, amely az alapok középpontjain halad át. Párhuzamos a generátorokkal.

Egy hengert egyenlő oldalúnak nevezünk, ha magassága megegyezik az alap átmérőjével.

Ha a henger alapjai laposak (és ezért az őket tartalmazó síkok párhuzamosak), akkor azt mondjuk, hogy a henger egy síkon áll. Ha egy síkon álló henger alapjai merőlegesek a generatrixra, akkor a hengert egyenesnek nevezzük.

Különösen, ha egy síkon álló henger alapja egy kör, akkor kör alakú (kör alakú) hengerről beszélünk; ha ellipszis, akkor ellipszis alakú.

1. 3. A henger szakaszai

A tengelyével párhuzamos síkú henger keresztmetszete téglalap (3. ábra, a). Két oldala a henger generátora, a másik kettő pedig az alapok párhuzamos húrjai.

A) b)

V) G)

Rizs. 3 – A henger szakaszai

Különösen a téglalap a tengelyirányú metszet. Ez egy hengerszakasz, amelynek tengelyén egy sík halad át (3. ábra, b).

Az alappal párhuzamos síkú henger keresztmetszete egy kör (3. ábra, c).

Az alappal és a tengelyével nem párhuzamos síkú henger keresztmetszete ovális (3d. ábra).

1. Tétel. A henger alapjának síkjával párhuzamos sík metszi a henger oldalfelületét az alap kerületével megegyező kör mentén.

Bizonyíték. Legyen β a henger alapjának síkjával párhuzamos sík. A hengertengely irányában történő párhuzamos transzláció, a β síkot a henger alapjának síkjával kombinálva az oldalfelület β sík szerinti metszetét egyesíti az alap kerületével. A tétel bizonyítást nyert.

A henger oldalsó felülete.

A henger oldalfelületének területe az a határ, amelyre a hengerbe írt szabályos prizma oldalfelületének területe hajlik, ha ennek a prizma alapjának oldalainak száma korlátlanul növekszik.

2. Tétel. Egy henger oldalfelületének területe egyenlő az alapja kerületének és magasságának szorzatával (S oldal.c = 2πRH, ahol R a henger alapjának sugara, H a henger magassága).

A) b)
Rizs. 4 − A henger oldalfelülete

Bizonyíték.

Legyen P n a hengerbe írt szabályos n-szögű prizma alap kerülete, illetve H magassága (4. ábra, a). Ekkor ennek a prizmának az oldalfelületének területe S oldal.c − P n H. Tegyük fel, hogy az alapba írt sokszög oldalainak száma korlátlanul növekszik (4. ábra, b). Ekkor a P n kerület a C = 2πR kerületre hajlik, ahol R a henger alapjának sugara, és a H magasság nem változik. Így a prizma oldalfelületének területe a 2πRH határáig tart, azaz a henger oldalfelületének területe egyenlő az S oldallal.c = 2πRH. A tétel bizonyítást nyert.

A henger teljes felülete.

Egy henger teljes felülete az oldalfelület és a két alap felületének összege. A henger minden alapterülete egyenlő πR 2-vel, ezért az S total henger teljes felületének területét az S oldal képlettel számítjuk ki.c = 2πRH+ 2πR 2.

r

T 1

T

F

F 1

F

T

A)

F

b)

Rizs. 5 − A henger teljes felülete

Ha a henger oldalfelületét az FT generatrix mentén levágjuk (5. ábra, a) és kihajtjuk úgy, hogy az összes generátor egy síkban legyen, akkor ennek eredményeként egy FTT1F1 téglalapot kapunk, amelyet a a henger oldalfelülete. A téglalap FF1 oldala a hengeralap körének kifejlődése, ezért FF1=2πR, oldala pedig FT egyenlő a henger generatrixával, azaz FT = H (5. ábra, b). Így a hengerfejlődés FT∙FF1=2πRH területe megegyezik az oldalfelületének területével.

1.5. Henger térfogata

Ha egy geometriai test egyszerű, azaz véges számú háromszög alakú piramisra osztható, akkor a térfogata megegyezik ezen piramisok térfogatának összegével. Tetszőleges test esetén a térfogatot a következőképpen határozzuk meg.

Egy adott testnek V térfogata van, ha vannak egyszerű testek, amelyek tartalmazzák, és vannak olyan egyszerű testek, amelyek térfogata a kívánt mértékben különbözik V-től.

Alkalmazzuk ezt a definíciót egy R alapsugárral és H magasságú henger térfogatának meghatározására.

A kör területének képletének származtatása során két n-szöget szerkesztettünk meg (az egyik a kört tartalmazza, a másik a körben), hogy területük n korlátlan növekedésével megközelítse a a kör korlátlanul. Szerkesszünk ilyen sokszögeket a henger alján lévő körhöz. Legyen P egy kört tartalmazó sokszög, és P" egy körben lévő sokszög (6. ábra).

Rizs. 7 − Henger, amelynek prizmája van leírt és beleírva

Készítsünk két egyenes prizmát P és P" alappal, és H magassággal egyenlő a henger magasságával. Az első prizma egy hengert, a második pedig egy hengert tartalmaz. Mivel n korlátlan növekedésével a a prizmák alapterületei korlátlanul megközelítik az S henger alapterületét, majd térfogatuk korlátlanul megközelíti az SH-t a definíció szerint a henger térfogatát

V = SH = πR 2 H.

Tehát egy henger térfogata megegyezik az alapterület és a magasság szorzatával.

1. feladat.

A henger tengelyirányú metszete Q területű négyzet.

Keresse meg a henger alapterületét.

Adott: henger, négyzet - a henger tengelyirányú metszete, S négyzet = Q.

Keresse meg: S főhenger

A tér oldala . Ez megegyezik az alap átmérőjével. Ezért az alap területe .

Válasz: S főhenger. =

2. feladat.

Egy hengerbe szabályos hatszögletű prizma van beírva. Határozza meg az oldallap átlója és a henger tengelye közötti szöget, ha az alap sugara megegyezik a henger magasságával!

Adott: henger, a hengerbe írt szabályos hatszögletű prizma, alapsugár = a henger magassága.

Keresse meg: az oldallap átlója és a henger tengelye közötti szög.

Megoldás: A prizma oldallapjai négyzetek, mivel egy szabályos hatszög körbe írt oldala megegyezik a sugárral.

A prizma élei párhuzamosak a hengertengellyel, ezért a homloklap átlója és a hengertengely közötti szög egyenlő az átló és az oldalél közötti szöggel. És ez a szög 45°, mivel a lapok négyzetek.

Válasz: az oldallap átlója és a henger tengelye közötti szög = 45°.

3. feladat.

A henger magassága 6 cm, az alap sugara 5 cm.

Keresse meg a henger tengelyével párhuzamosan megrajzolt szakasz területét, attól 4 cm távolságra.

Adott: H = 6 cm, R = 5 cm, OE = 4 cm.

Keresés: S mp.

S mp. = KM×KS,

OE = 4 cm, KS = 6 cm.

OKM háromszög - egyenlő szárú (OK = OM = R = 5 cm),

Az OEK háromszög derékszögű.

Az OEK háromszögből a Pitagorasz-tétel szerint:

KM = 2EK = 2 × 3 = 6,

S mp. = 6×6 = 36 cm 2.

Ennek az esszének a célja megvalósult egy geometriai testet, például egy hengert.

A következő feladatokat veszik figyelembe:

− megadjuk a henger definícióját;

− figyelembe veszik a henger elemeit;

− a henger tulajdonságait tanulmányoztuk;

− figyelembe veszik a hengerszelvények típusait;

- levezetik a henger területének képletét;

− levezetjük a henger térfogatának képletét;

− problémákat oldott meg henger segítségével.

1. Pogorelov A.V. Geometria: Tankönyv 10-11 évfolyamos oktatási intézmények számára, 1995.

2. Beskin L.N. Sztereometria. Kézikönyv középiskolai tanároknak, 1999.

3. Atanasyan L. S., Butuzov V. F., Kadomtsev S. B., Kiseleva L. S., Poznyak E. G. Geometry: Tankönyv az oktatási intézmények 10-11. osztályai számára, 2000.

4. Aleksandrov A.D., Werner A.L., Ryzhik V.I. Geometria: tankönyv 10-11 évfolyamos általános oktatási intézményekben, 1998.

5. Kiselev A. P., Rybkin N. A. Geometria: Sztereometria: 10 – 11 évfolyam: Tankönyv és feladatfüzet, 2000.