Distance and Length Units Converter Area Units Converter Join © 2011-2017 Mikhail Dovzhik Copying of materials is prohibited. In the online calculator, you can use values ​​in the same units of measurement! If you have trouble converting units of measure, use the Distance and Length Unit Converter and the Area Unit Converter. Additional features of the quadrilateral area calculator

• You can move between input fields by pressing the right and left keys on the keyboard.

Theory. Area of ​​a quadrilateral A quadrilateral is a geometric figure consisting of four points (vertices), no three of which lie on the same straight line, and four segments (sides) connecting these points in pairs. A quadrilateral is called convex if the segment connecting any two points of this quadrilateral will be inside it.

How to find the area of ​​a polygon?

The formula for determining the area is determined by taking each edge of the polygon AB, and calculating the area of ​​the triangle ABO with a vertex at the origin O, through the coordinates of the vertices. When walking around a polygon, triangles are formed, including the inside of the polygon and located outside it. The difference between the sum of these areas is the area of ​​the polygon itself.

Therefore, the formula is called the surveyor's formula, since the "cartographer" is at the origin; if it walks the area counterclockwise, the area is added if it's on the left and subtracted if it's on the right in terms of the origin. The area formula is valid for any non-intersecting (simple) polygon, which may be convex or concave. Content

• 1 Definition
• 2 Examples
• 3 More complex example
• 4 Name explanation
• 5 See

Polygon area

Attention

It could be:

• triangle;
• quadrilateral;
• five- or hexagon and so on.

Such a figure will certainly be characterized by two positions:

1. Adjacent sides do not belong to the same line.
2. Non-adjacent ones have no common points, that is, they do not intersect.

To understand which vertices are adjacent, you need to see if they belong to the same side. If yes, then neighboring. Otherwise, they can be connected by a segment, which must be called a diagonal. They can only be drawn in polygons that have more than three vertices.

What kinds of them exist? A polygon with more than four corners can be convex or concave. The difference of the latter is that some of its vertices may lie on different sides of a straight line drawn through an arbitrary side of the polygon.

How to find the area of ​​a regular and irregular hexagon?

• Knowing the length of the side, multiply it by 6 and get the perimeter of the hexagon: 10 cm x 6 \u003d 60 cm
• Substitute the results in our formula:
Area \u003d 1/2 * perimeter * apothema Area \u003d ½ * 60cm * 5√3 Solve: Now it remains to simplify the answer to get rid of square roots, and indicate the result in square centimeters: ½ * 60 cm * 5√3 cm \u003d 30 * 5√3 cm =150 √3 cm =259.8 cm² Video on how to find the area of ​​a regular hexagon There are several options for determining the area of ​​an irregular hexagon:

• trapezoid method.
• A method for calculating the area of ​​irregular polygons using the coordinate axis.
• A method for splitting a hexagon into other shapes.

Depending on the initial data that you will know, the appropriate method is selected.

Important

Some irregular hexagons consist of two parallelograms. To determine the area of ​​a parallelogram, multiply its length by its width and then add the two already known areas. Video on how to find the area of ​​a polygon An equilateral hexagon has six equal sides and is a regular hexagon.

The area of ​​an equilateral hexagon is equal to 6 areas of the triangles into which a regular hexagonal figure is divided. All triangles in a regular hexagon are equal, so to find the area of ​​such a hexagon, it will be enough to know the area of ​​at least one triangle. To find the area of ​​an equilateral hexagon, of course, the formula for the area of ​​a regular hexagon, described above, is used.

404 not found

Decorating a home, clothing, drawing pictures contributed to the process of formation and accumulation of information in the field of geometry, which people of those times obtained empirically, bit by bit and passed on from generation to generation. Today, knowledge of geometry is necessary for a cutter, a builder, an architect, and every ordinary person in everyday life. Therefore, you need to learn how to calculate the area of ​​\u200b\u200bdifferent figures, and remember that each of the formulas can be useful later in practice, including the formula for a regular hexagon.
A hexagon is such a polygonal figure, the total number of angles of which is six. A regular hexagon is a hexagonal figure that has equal sides. The angles of a regular hexagon are also equal to each other.
In everyday life, we can often find objects that have the shape of a regular hexagon.

Irregular polygon area calculator by sides

You will need

• - roulette;
• — electronic rangefinder;
• - a sheet of paper and a pencil;
• - calculator.

Instruction 1 If you need the total area of ​​​​an apartment or a separate room, just read the technical passport for the apartment or house, it shows the footage of each room and the total footage of the apartment. 2 To measure the area of ​​a rectangular or square room, take a tape measure or an electronic rangefinder and measure the length of the walls. When measuring distances with a rangefinder, be sure to keep the beam direction perpendicular, otherwise the measurement results may be distorted. 3 Then multiply the resulting length (in meters) of the room by the width (in meters). The resulting value will be the floor area, it is measured in square meters.

Gauss area formula

If you need to calculate the floor area of ​​a more complex structure, such as a pentagonal room or a room with a round arch, sketch a schematic sketch on a piece of paper. Then divide the complex shape into several simple ones, such as a square and a triangle, or a rectangle and a semicircle. Use a tape measure or rangefinder to measure the size of all sides of the resulting figures (for a circle, you need to know the diameter) and enter the results on your drawing.

5 Now calculate the area of ​​each shape separately. The area of ​​rectangles and squares is calculated by multiplying the sides. To calculate the area of ​​a circle, divide the diameter in half and square (multiply it by itself), then multiply the result by 3.14.
If you only want half of the circle, divide the resulting area in half. To calculate the area of ​​a triangle, find P by dividing the sum of all sides by 2.

Formula for calculating the area of ​​an irregular polygon

If the points are numbered sequentially in a counterclockwise direction, then the determinants in the formula above are positive and the modulus in it can be omitted; if they are numbered in a clockwise direction, the determinants will be negative. This is because the formula can be viewed as a special case of Green's theorem. To apply the formula, you need to know the coordinates of the polygon vertices in the Cartesian plane.

For example, let's take a triangle with coordinates ((2, 1), (4, 5), (7, 8)). Take the first x-coordinate of the first vertex and multiply it by the y-coordinate of the second vertex, and then multiply the x-coordinate of the second vertex by the y-coordinate of the third. We repeat this procedure for all vertices. The result can be determined by the following formula: A tri.

The formula for calculating the area of ​​an irregular quadrilateral

A) _(\text(tri.))=(1 \over 2)|x_(1)y_(2)+x_(2)y_(3)+x_(3)y_(1)-x_(2) y_(1)-x_(3)y_(2)-x_(1)y_(3)|) where xi and yi denote the corresponding coordinate. This formula can be obtained by opening the brackets in the general formula for the case n = 3. Using this formula, you can find that the area of ​​a triangle is equal to half the sum of 10 + 32 + 7 - 4 - 35 - 16, which gives 3. The number of variables in the formula depends on the number of sides of the polygon. For example, the formula for the area of ​​a pentagon will use variables up to x5 and y5: A pent. = 1 2 | x 1 y 2 + x 2 y 3 + x 3 y 4 + x 4 y 5 + x 5 y 1 − x 2 y 1 − x 3 y 2 − x 4 y 3 − x 5 y 4 − x 1 y 5 | (\displaystyle \mathbf (A) _(\text(pent.))=(1 \over 2)|x_(1)y_(2)+x_(2)y_(3)+x_(3)y_(4 )+x_(4)y_(5)+x_(5)y_(1)-x_(2)y_(1)-x_(3)y_(2)-x_(4)y_(3)-x_(5 )y_(4)-x_(1)y_(5)|) A for a quad - variables up to x4 and y4: A quad.

A hexagon or hexagon is a regular polygon whose sides are equal to each other, and each angle is exactly 120 degrees. A hexagon is sometimes found in human everyday life, so you may need to calculate its area not only in school problems, but also in real life.

convex hexagon

Heskagon is a regular convex polygon, respectively, all its angles are equal, all sides are equal, and if you draw a segment through two adjacent vertices, then the whole figure will be on one side of this segment. As in any regular n-gon, a circle can be described around the hexagon or inscribed inside it. The main feature of a hexagon is that the length of the radius of the circumscribed circle coincides with the length of the side of the polygon. Thanks to this property, you can easily find the area of ​​a hexagon using the formula:

S \u003d 2.59 R 2 \u003d 2.59 a 2.

In addition, the radius of the inscribed circle is related to the side of the figure as:

It follows that the area of ​​a hexagon can be calculated using one of three variables to choose from.

Hexagram

The stellated regular hexagon appears before us in the form of a six-pointed star. Such a figure is formed by superimposing two equilateral triangles on top of each other. The most famous real hexagram is the Star of David - the symbol of the Jewish people.

Hexagonal numbers

In number theory, there are figurative numbers associated with certain geometric shapes. The most widely used are triangular and square, as well as tetrahedral and pyramidal numbers, using which it is easy to lay out geometric shapes using real objects. For example, pyramidal numbers will tell you how to stack cannonballs into a stable pyramid. There are also hexagonal numbers that determine the number of points required to build a hexagon.

Hexagon in reality

Hexagons are often seen in real life. For example, the sections of nuts or pencils are hexagonal, which provides a comfortable grip on the object. The hexagon is an effective geometric figure capable of tiling a plane without gaps or overlaps. That is why decorative finishing materials, for example, tiles and paving slabs or plasterboard panels, often have a hexagonal shape.

The efficiency of the hexagon makes it popular in nature as well. Honeycombs have exactly a hexagonal shape, thanks to which the space of the hive is filled without gaps. Another example of a hexagonal tiling of a plane is the Giant's Trail - a wildlife monument formed during a volcanic eruption. Volcanic ash was compressed into hexagonal columns that paved the surface of the coast of Northern Ireland.

Packing circles on a plane

And a little more about the effectiveness of the hexagon. Packing balls is a classic combinatorial geometry problem that requires finding the best way to pack non-intersecting balls. In practice, this task turns into a logistical problem of packing oranges, apples, cannonballs, or any other spherical object that needs to be packed as tightly as possible. Heskagon is the solution to this problem.

It is known that the most efficient arrangement of circles in two-dimensional space is to place the centers of the circles on the vertices of hexagons that fill the plane without gaps. In 3D reality, the problem of placing balls is solved by stacking objects hexagonally.

Using our calculator, you can calculate the area of ​​a regular hexagon by knowing its side or the radii of the corresponding circles. Let's try to calculate the areas of hexagons using real examples.

Real life examples

giant hexagon

The giant hexagon is a unique atmospheric phenomenon on Saturn that looks like a grand vortex in the shape of a regular hexagon. It is known that the side of the giant hexagon is 13,800 km, thanks to which we can determine the area of ​​the "cloud". To do this, just enter the value of the side into the calculator form and get the result:

Thus, the area of ​​the atmospheric vortex on Saturn is approximately 494,777,633 square kilometers. Truly impressive.

Hexagonal chess

We are all accustomed to the chess field, divided into 64 square cells. However, there are also hexagonal chess, the playing field of which is divided into 91 regular hexagons. Let's determine the area of ​​the game board for the hexagonal version of the famous game. Let the side of the cell be 2 centimeters. The area of ​​one game cell will be:

Then the area of ​​the entire board will be equal to 91 × 10.39 = 945.49 square centimeters.

Conclusion

The hexagon is often found in reality, although we do not notice it. Use our online calculator to calculate the area of ​​hexagons for everyday or school problems.

A hexagon is a polygon with 6 sides and 6 angles. Depending on whether a hexagon is regular or not, there are several methods for finding its area. We will review everything.

How to find the area of ​​a regular hexagon

Formulas for calculating the area of ​​a regular hexagon - a convex polygon with six identical sides.

Given side length:

• Area formula: S = (3√3*a²)/2
• If the length of the side a is known, then substituting it into the formula, we can easily find the area of ​​​​the figure.
• Otherwise, the length of the side can be found through the perimeter and apothem.
• If the perimeter is given, then we simply divide it by 6 and get the length of one side. For example, if the perimeter is 24, then the side length will be 24/6 = 4.
• Apothem is a perpendicular drawn from the center to one of the sides. To find the length of one side, we substitute the length of the apothem into the formula a = 2*m/√3. That is, if the apothem m = 2√3, then the length of the side a = 2*2√3/√3 = 4.

Given an apothem:

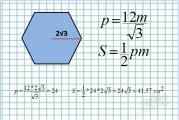
• Area formula: S = 1/2*p*m, where p is the perimeter, m is the apothem.
• Let us find the perimeter of the hexagon through the apothem. In the previous paragraph, we learned how to find the length of one side through an apothem: a \u003d 2 * m / √3. It remains only to multiply this result by 6. We get the perimeter formula: p \u003d 12 * m / √3.

Given the radius of the circumscribed circle:

• The radius of a circle circumscribed around a regular hexagon is equal to the side of this hexagon.
  Area formula: S = (3√3*a²)/2

Given the radius of the inscribed circle:

• Area formula: S = 3√3*r², where r = √3*a/2 (a is one of the sides of the polygon).

How to find the area of ​​an irregular hexagon

Formulas for calculating the area of ​​​​an irregular hexagon - a polygon whose sides are not equal to each other.

Trapeze method:

• We divide the hexagon into arbitrary trapezoids, calculate the area of ​​each of them and add them up.
• Basic formulas for the area of ​​a trapezoid: S = 1/2*(a + b)*h, where a and b are the bases of the trapezoid, h is the height.
  S = h*m, where h is the height, m ​​is the midline.

The coordinates of the vertices of the hexagon are known:

• To begin with, let's write down the coordinates of the points, moreover, placing them not in a chaotic order, but sequentially one after another. For example:
  A: (-3, -2)
  B: (-1, 4)
  C: (6, 1)
  D: (3, 10)
  E: (-4, 9)
  F: (-5, 6)
• Next, carefully, multiply the x-coordinate of each point by the y-coordinate of the next point:
  -3*4 = -12
  -1*1 = -1
  6*10 = 60
  3*9 = 27
  -4*6 = -24
  -5*(-2) = 10
  Add up the results:
  -12 – 1 + 60 + 27 – 24 + 10 = 60
  Next, multiply the y-coordinate of each point by the x-coordinate of the next point.
  -2*(-1) = 2
  4*6 = 24
  1*3 = 3
  10*(-4) = -40
  9*(-5) = -45
  6*(-3) = -18
  Add up the results:
  2 + 24 + 3 – 40 – 45 – 18 = -74
  Subtract the second from the first result:
  60 -(-74) = 60 + 74 = 134
  The resulting number is divided by two:
  134/2 = 67
  Answer: 67 square units.

• Also, to find the area of ​​a hexagon, you can break it into triangles, squares, rectangles, parallelograms, and so on. Find the areas of its constituent figures and add them up.

So, the methods for finding the area of ​​a hexagon for all occasions have been studied. Now go ahead and apply what you've learned! Good luck!

The topic of polygons is covered in the school curriculum, but they do not pay enough attention to it. Meanwhile, it is interesting, and this is especially true of a regular hexagon or hexagon - after all, many natural objects have this shape. These include honeycombs and more. This form is very well applied in practice.

Definition and construction

A regular hexagon is a plane figure that has six sides equal in length and the same number of equal angles.

If we recall the formula for the sum of the angles of a polygon

it turns out that in this figure it is equal to 720 °. Well, since all the angles of the figure are equal, it is easy to calculate that each of them is equal to 120 °.

Drawing a hexagon is very simple, all you need is a compass and a ruler.

The step by step instructions will look like this:

If desired, you can do without a line by drawing five circles of equal radius.

The figure thus obtained will be a regular hexagon, and this can be proved below.

Properties are simple and interesting

To understand the properties of a regular hexagon, it makes sense to break it into six triangles:

This will help in the future to more clearly display its properties, the main of which are:

1. circumscribed circle diameter;
2. diameter of the inscribed circle;
3. square;
4. perimeter.

The circumscribed circle and the possibility of construction

It is possible to describe a circle around a hexagon, and moreover, only one. Since this figure is correct, you can do it quite simply: draw a bisector from two adjacent angles inside. They intersect at point O, and together with the side between them form a triangle.

The angles between the side of the hexagon and the bisectors will be 60° each, so we can definitely say that a triangle, for example, AOB, is isosceles. And since the third angle will also be equal to 60 °, it is also equilateral. It follows that the segments OA and OB are equal, which means that they can serve as the radius of the circle.

After that, you can go to the next side, and also draw a bisector from the angle at point C. It will turn out another equilateral triangle, and side AB will be common to two at once, and OS will be the next radius through which the same circle goes. There will be six such triangles in total, and they will have a common vertex at point O. It turns out that it will be possible to describe the circle, and it is only one, and its radius is equal to the side of the hexagon:

That is why it is possible to construct this figure with the help of a compass and a ruler.

Well, the area of ​​\u200b\u200bthis circle will be standard:

Inscribed circle

The center of the circumscribed circle coincides with the center of the inscribed one. To verify this, we can draw perpendiculars from the point O to the sides of the hexagon. They will be the heights of those triangles that make up the hexagon. And in an isosceles triangle, the height is the median with respect to the side on which it rests. Thus, this height is nothing but the perpendicular bisector, which is the radius of the inscribed circle.

The height of an equilateral triangle is calculated simply:

h²=a²-(a/2)²= a²3/4, h=a(√3)/2

And since R=a and r=h, it turns out that

r=R(√3)/2.

Thus, the inscribed circle passes through the centers of the sides of a regular hexagon.

Its area will be:

S=3πa²/4,

that is, three-quarters of that described.

Perimeter and area

Everything is clear with the perimeter, this is the sum of the lengths of the sides:

P=6a, or P=6R

But the area will be equal to the sum of all six triangles into which the hexagon can be divided. Since the area of ​​a triangle is calculated as half the product of the base and the height, then:

S \u003d 6 (a / 2) (a (√3) / 2) \u003d 6a² (√3) / 4 \u003d 3a² (√3) / 2 or

S=3R²(√3)/2

Those who wish to calculate this area through the radius of the inscribed circle can be done like this:

S=3(2r/√3)²(√3)/2=r²(2√3)

Entertaining constructions

A triangle can be inscribed in a hexagon, the sides of which will connect the vertices through one:

There will be two of them in total, and their imposition on each other will give the Star of David. Each of these triangles is equilateral. This is easy to verify. If you look at the AC side, then it belongs to two triangles at once - BAC and AEC. If in the first of them AB \u003d BC, and the angle between them is 120 °, then each of the remaining ones will be 30 °. From this we can draw logical conclusions:

1. The height of ABC from vertex B will be equal to half the side of the hexagon, since sin30°=1/2. Those who wish to verify this can be advised to recalculate according to the Pythagorean theorem, it fits here perfectly.
2. The AC side will be equal to two radii of the inscribed circle, which is again calculated using the same theorem. That is, AC=2(a(√3)/2)=а(√3).
3. Triangles ABC, CDE and AEF are equal in two sides and the angle between them, and hence the equality of sides AC, CE and EA follows.

Intersecting with each other, the triangles form a new hexagon, and it is also regular. It's easy to prove:

Thus, the figure meets the signs of a regular hexagon - it has six equal sides and angles. From the equality of triangles at the vertices, it is easy to deduce the length of the side of the new hexagon:

d=а(√3)/3

It will also be the radius of the circle described around it. The radius of the inscribed will be half the side of the large hexagon, which was proved when considering the triangle ABC. Its height is exactly half of the side, therefore, the second half is the radius of the circle inscribed in the small hexagon:

r₂=а/2

S=(3(√3)/2)(а(√3)/3)²=а(√3)/2

It turns out that the area of ​​​​the hexagon inside the star of David is three times smaller than that of the large one in which the star is inscribed.

From theory to practice

The properties of the hexagon are very actively used both in nature and in various fields of human activity. First of all, this applies to bolts and nuts - the hats of the first and second are nothing more than a regular hexagon, if you do not take into account the chamfers. The size of wrenches corresponds to the diameter of the inscribed circle - that is, the distance between opposite faces.

Has found its application and hexagonal tiles. It is much less common than a quadrangular one, but it is more convenient to lay it: three tiles meet at one point, not four. Compositions can be very interesting:

Concrete paving slabs are also produced.

The prevalence of the hexagon in nature is explained simply. Thus, it is easiest to fit circles and balls tightly on a plane if they have the same diameter. Because of this, honeycombs have such a shape.

Mathematical properties

A feature of a regular hexagon is the equality of its side and the radius of the circumscribed circle, since

All angles are 120°.

The radius of the inscribed circle is:

The perimeter of a regular hexagon is:

The area of ​​a regular hexagon is calculated by the formulas:

Hexagons tiling the plane, that is, they can fill the plane without gaps and overlaps, forming the so-called parquet.

Hexagonal parquet (hexagonal parquet)- tessellation of the plane with equal regular hexagons located side to side.

Hexagonal parquet is dual to triangular parquet: if you connect the centers of adjacent hexagons, then the segments drawn will give a triangular parquet. The Schläfli symbol of a hexagonal parquet is (6,3), which means that three hexagons converge at each vertex of the parquet.

Hexagonal parquet is the most dense packing of circles on the plane. In two-dimensional Euclidean space, the best filling is to place the centers of the circles at the vertices of a parquet formed by regular hexagons, in which each circle is surrounded by six others. The density of this packing is . In 1940, it was proved that this packing is the densest.

A regular hexagon with a side is a universal cover, that is, any set of diameter can be covered by a regular hexagon with a side (Pal's lemma).

A regular hexagon can be constructed using a compass and straightedge. Below is the construction method proposed by Euclid in the Elements, Book IV, Theorem 15.

Regular hexagon in nature, technology and culture

show the partition of the plane into regular hexagons. The hexagonal shape more than the others allows you to save on the walls, that is, less wax will be spent on honeycombs with such cells.

Some complex crystals and molecules, such as graphite, have a hexagonal crystal lattice.

Formed when microscopic water droplets in clouds are attracted to dust particles and freeze. The ice crystals that appear in this case, which at first do not exceed 0.1 mm in diameter, fall down and grow as a result of condensation of moisture from the air on them. In this case, six-pointed crystalline forms are formed. Due to the structure of water molecules, only 60° and 120° angles are possible between the rays of the crystal. The main water crystal has the shape of a regular hexagon in the plane. New crystals are then deposited on the tops of such a hexagon, new ones are deposited on them, and thus various forms of snowflake stars are obtained.

Scientists from the University of Oxford were able to simulate the emergence of such a hexagon in the laboratory. To find out how such a formation occurs, the researchers placed a 30-liter bottle of water on a turntable. She modeled the atmosphere of Saturn and its usual rotation. Inside, scientists placed small rings that rotate faster than the container. This generated miniature eddies and jets, which the experimenters visualized with green paint. The faster the ring rotated, the larger the eddies became, causing the nearby stream to deviate from a circular shape. Thus, the authors of the experiment managed to obtain various shapes - ovals, triangles, squares and, of course, the desired hexagon.

A natural monument of about 40,000 interconnected basalt (rarely andesitic) columns, formed as a result of an ancient volcanic eruption. Located in the north-east of Northern Ireland, 3 km north of the city of Bushmills.

The tops of the columns form a kind of springboard, which starts at the foot of the cliff and disappears under the surface of the sea. Most of the columns are hexagonal, although some have four, five, seven or eight corners. The tallest column is about 12 meters high.

About 50-60 million years ago, during the Paleogene period, the Antrim site was subject to intense volcanic activity when molten basalt permeated through the deposits, forming extensive lava plateaus. With rapid cooling, the volume of the substance decreased (this is observed when the mud dries). Horizontal compression resulted in the characteristic structure of hexagonal pillars.

The cross section of the nut has the form of a regular hexagon.