Logarithm of the number 8 to base 3. What is a logarithm. Examples of solving logarithms

Health

Algebra is a complex and interesting science based on many functions. Let's look at what a logarithm is and what its properties are.

A logarithm is the power to which the number a must be raised to obtain the number x.

Algebra knows many types of logarithms. The most common types of logarithms are:

natural with base e=2.718281, denoted by ln.
Example: ln1=0. lne=1;
decimal with base 10, denoted lg.
Example: lg100=2. log 10 100=2, since 10 2 =100;
binary, denoted lb(b) or lb 2 b. Is the solution to the equation 2 x =b.
Example: lb16=4.

The latter are widely used in computer science, information theory, as well as many subfields of discrete mathematics. Logarithms help statistical scientists determine the most important probability distributions. They are also used in genetics.

Counting using logarithms

Mathematicians have long been aware of the unique properties of logarithms, as well as the possibility of using them to simplify complex calculations. So, when moving to logarithms:

multiplication is easily replaced by addition;
division - by subtraction;
raising to a certain power or taking a root becomes multiplication or division.

When counting using logarithms, you should get rid of the log sign. Wherein:

The reason and argument must be positive;
The base must be different from one, since this number, raised to any power, remains unchanged.

Logarithmic function

The logarithmic function y = loga x (where a > 0, a ≠ 1) is also used in calculations. Among its properties are the following:

the domain of definition of this function lies in the set of positive numbers;
the set of function values is represented by real numbers;
the function does not have a maximum or minimum value;
the function belongs to the general form, not being even or odd;
the function is not periodic;
the graph passes through the coordinate axes at point (1;0);
if the base is greater than one, the function increases, and if it is less than one, it decreases.

Now you have an idea of logarithms, their scope, as well as the properties of the logarithmic function.

The logarithm of a number b to base a is the exponent to which the number a must be raised to obtain the number b.

If, then.

Logarithm - extreme important mathematical quantity, since logarithmic calculus allows not only solving exponential equations, but also operating with exponents, differentiating exponential and logarithmic functions, integrating them and leading them to a more acceptable form to be calculated.

In contact with

All properties of logarithms are directly related to the properties of exponential functions. For example, the fact that means that:

It should be noted that when solving specific problems, the properties of logarithms may turn out to be more important and useful than the rules for working with powers.

Let us present some identities:

Here are the basic algebraic expressions:

;

Attention! can exist only for x>0, x≠1, y>0.

Let's try to understand the question of what natural logarithms are. Special interest in mathematics represent two types- the first one has the number “10” as its base, and is called the “decimal logarithm”. The second one is called natural. The base of the natural logarithm is the number “e”. This is what we will talk about in detail in this article.

Designations:

lg x - decimal;
ln x - natural.

Using the identity, we can see that ln e = 1, as well as the fact that lg 10=1.

Natural logarithm graph

Let's construct a graph of the natural logarithm using the standard classical method point by point. If you wish, you can check whether we are constructing the function correctly by examining the function. However, it makes sense to learn how to build it “manually” in order to know how to correctly calculate the logarithm.

Function: y = ln x. Let's write down a table of points through which the graph will pass:

Let us explain why we chose these particular values of the argument x. It's all about identity: . For the natural logarithm this identity will look like this:

For convenience, we can take five reference points:

;

Thus, calculating natural logarithms is a fairly simple task; moreover, it simplifies calculations of operations with powers, turning them into ordinary multiplication.

By plotting a graph point by point, we get an approximate graph:

The domain of definition of the natural logarithm (i.e., all valid values of the argument X) is all numbers greater than zero.

Attention! The domain of definition of the natural logarithm includes only positive numbers! The scope of definition does not include x=0. This is impossible based on the conditions for the existence of the logarithm.

The range of values (i.e. all valid values of the function y = ln x) is all numbers in the interval.

Natural log limit

Studying the graph, the question arises - how does the function behave at y<0.

Obviously, the graph of the function tends to cross the y-axis, but will not be able to do this, since the natural logarithm of x<0 не существует.

Limit of natural log can be written this way:

Formula for replacing the base of a logarithm

Dealing with a natural logarithm is much easier than dealing with a logarithm that has an arbitrary base. That is why we will try to learn how to reduce any logarithm to a natural one, or express it to an arbitrary base through natural logarithms.

Let's start with the logarithmic identity:

Then any number or variable y can be represented as:

where x is any number (positive according to the properties of the logarithm).

This expression can be taken logarithmically on both sides. Let's do this using an arbitrary base z:

Let’s use the property (only instead of “c” we have the expression):

From here we get the universal formula:

In particular, if z=e, then:

We were able to represent a logarithm to an arbitrary base through the ratio of two natural logarithms.

We solve problems

In order to better understand natural logarithms, let's look at examples of several problems.

Problem 1. It is necessary to solve the equation ln x = 3.

Solution: Using the definition of the logarithm: if , then , we get:

Problem 2. Solve the equation (5 + 3 * ln (x - 3)) = 3.

Solution: Using the definition of the logarithm: if , then , we get:

Let's use the definition of a logarithm again:

Thus:

You can approximately calculate the answer, or you can leave it in this form.

Task 3. Solve the equation.

Solution: Let's make a substitution: t = ln x. Then the equation will take the following form:

We have a quadratic equation. Let's find its discriminant:

In statistics and probability theory, logarithmic quantities are found very often. This is not surprising, because the number e often reflects the growth rate of exponential quantities.

In computer science, programming and computer theory, logarithms are encountered quite often, for example, in order to store N bits in memory.

In the theories of fractals and dimensions, logarithms are constantly used, since the dimensions of fractals are determined only with their help.

In mechanics and physics There is no section where logarithms were not used. Barometric distribution, all the principles of statistical thermodynamics, the Tsiolkovsky equation, etc. are processes that can be mathematically described only using logarithms.

In chemistry, logarithms are used in Nernst equations and descriptions of redox processes.

Amazingly, even in music, in order to find out the number of parts of an octave, logarithms are used.

Natural logarithm Function y=ln x its properties

Proof of the main property of the natural logarithm

main properties.

logax + logay = loga(x y);
logax − logay = loga (x: y).

identical grounds

Log6 4 + log6 9.

Now let's complicate the task a little.

Examples of solving logarithms

What if the base or argument of a logarithm is a power? Then the exponent of this degree can be taken out of the sign of the logarithm according to the following rules:

Of course, all these rules make sense if the ODZ of the logarithm is observed: a > 0, a ≠ 1, x >

Task. Find the meaning of the expression:

Transition to a new foundation

Let the logarithm logax be given. Then for any number c such that c > 0 and c ≠ 1, the equality is true:

Task. Find the meaning of the expression:

Basic properties of the logarithm

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

The exponent is 2.718281828…. To remember the exponent, you can study the rule: the exponent is equal to 2.7 and twice the year of birth of Leo Nikolaevich Tolstoy.

Basic properties of logarithms

Knowing this rule, you will know both the exact value of the exponent and the date of birth of Leo Tolstoy.

Examples for logarithms

Logarithm expressions

Example 1.
A). x=10ac^2 (a>0,c>0).

Using properties 3.5 we calculate

4. Where .

Example 2. Find x if

Example 3. Let the value of logarithms be given

Calculate log(x) if

Basic properties of logarithms

Logarithms, like any numbers, can be added, subtracted and transformed in every way. But since logarithms are not exactly ordinary numbers, there are rules here, which are called main properties.

You definitely need to know these rules - without them, not a single serious logarithmic problem can be solved. In addition, there are very few of them - you can learn everything in one day. So let's get started.

Adding and subtracting logarithms

Consider two logarithms with the same bases: logax and logay. Then they can be added and subtracted, and:

logax + logay = loga(x y);
logax − logay = loga (x: y).

So, the sum of logarithms is equal to the logarithm of the product, and the difference is equal to the logarithm of the quotient. Please note: the key point here is identical grounds. If the reasons are different, these rules do not work!

These formulas will help you calculate a logarithmic expression even when its individual parts are not considered (see the lesson “What is a logarithm”). Take a look at the examples and see:

Since logarithms have the same bases, we use the sum formula:
log6 4 + log6 9 = log6 (4 9) = log6 36 = 2.

Task. Find the value of the expression: log2 48 − log2 3.

The bases are the same, we use the difference formula:
log2 48 − log2 3 = log2 (48: 3) = log2 16 = 4.

Task. Find the value of the expression: log3 135 − log3 5.

Again the bases are the same, so we have:
log3 135 − log3 5 = log3 (135: 5) = log3 27 = 3.

As you can see, the original expressions are made up of “bad” logarithms, which are not calculated separately. But after the transformations, completely normal numbers are obtained. Many tests are based on this fact. Yes, test-like expressions are offered in all seriousness (sometimes with virtually no changes) on the Unified State Examination.

Extracting the exponent from the logarithm

It is easy to see that the last rule follows the first two. But it’s better to remember it anyway - in some cases it will significantly reduce the amount of calculations.

Of course, all these rules make sense if the ODZ of the logarithm is observed: a > 0, a ≠ 1, x > 0. And one more thing: learn to apply all formulas not only from left to right, but also vice versa, i.e. You can enter the numbers before the logarithm sign into the logarithm itself. This is what is most often required.

Task. Find the value of the expression: log7 496.

Let's get rid of the degree in the argument using the first formula:
log7 496 = 6 log7 49 = 6 2 = 12

Task. Find the meaning of the expression:

Note that the denominator contains a logarithm, the base and argument of which are exact powers: 16 = 24; 49 = 72. We have:

I think the last example requires some clarification. Where have logarithms gone? Until the very last moment we work only with the denominator.

Logarithm formulas. Logarithms examples solutions.

We presented the base and argument of the logarithm standing there in the form of powers and took out the exponents - we got a “three-story” fraction.

Now let's look at the main fraction. The numerator and denominator contain the same number: log2 7. Since log2 7 ≠ 0, we can reduce the fraction - 2/4 will remain in the denominator. According to the rules of arithmetic, the four can be transferred to the numerator, which is what was done. The result was the answer: 2.

Transition to a new foundation

Speaking about the rules for adding and subtracting logarithms, I specifically emphasized that they only work with the same bases. What if the reasons are different? What if they are not exact powers of the same number?

Formulas for transition to a new foundation come to the rescue. Let us formulate them in the form of a theorem:

Let the logarithm logax be given. Then for any number c such that c > 0 and c ≠ 1, the equality is true:

In particular, if we set c = x, we get:

From the second formula it follows that the base and argument of the logarithm can be swapped, but in this case the entire expression is “turned over”, i.e. the logarithm appears in the denominator.

These formulas are rarely found in ordinary numerical expressions. It is possible to evaluate how convenient they are only when solving logarithmic equations and inequalities.

However, there are problems that cannot be solved at all except by moving to a new foundation. Let's look at a couple of these:

Task. Find the value of the expression: log5 16 log2 25.

Note that the arguments of both logarithms contain exact powers. Let's take out the indicators: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;

Now let’s “reverse” the second logarithm:

Since the product does not change when rearranging factors, we calmly multiplied four and two, and then dealt with logarithms.

Task. Find the value of the expression: log9 100 lg 3.

The base and argument of the first logarithm are exact powers. Let's write this down and get rid of the indicators:

Now let's get rid of the decimal logarithm by moving to a new base:

Basic logarithmic identity

Often in the solution process it is necessary to represent a number as a logarithm to a given base. In this case, the following formulas will help us:

In the first case, the number n becomes the exponent in the argument. The number n can be absolutely anything, because it is just a logarithm value.

The second formula is actually a paraphrased definition. That's what it's called: .

In fact, what happens if the number b is raised to such a power that the number b to this power gives the number a? That's right: the result is the same number a. Read this paragraph carefully again - many people get stuck on it.

Like formulas for moving to a new base, the basic logarithmic identity is sometimes the only possible solution.

Task. Find the meaning of the expression:

Note that log25 64 = log5 8 - simply took the square from the base and argument of the logarithm. Taking into account the rules for multiplying powers with the same base, we get:

If anyone doesn’t know, this was a real task from the Unified State Exam :)

Logarithmic unit and logarithmic zero

In conclusion, I will give two identities that can hardly be called properties - rather, they are consequences of the definition of the logarithm. They constantly appear in problems and, surprisingly, create problems even for “advanced” students.

logaa = 1 is. Remember once and for all: the logarithm to any base a of that base itself is equal to one.
loga 1 = 0 is. The base a can be anything, but if the argument contains one, the logarithm is equal to zero! Because a0 = 1 is a direct consequence of the definition.

That's all the properties. Be sure to practice putting them into practice! Download the cheat sheet at the beginning of the lesson, print it out, and solve the problems.

Basic properties of the logarithm

It is necessary to know the above properties, since almost all problems and examples related to logarithms are solved on their basis. The rest of the exotic properties can be derived through mathematical manipulations with these formulas

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

When calculating the formula for the sum and difference of logarithms (3.4) you come across quite often. The rest are somewhat complex, but in a number of tasks they are indispensable for simplifying complex expressions and calculating their values.

Common cases of logarithms

Some of the common logarithms are those in which the base is even ten, exponential or two.
The logarithm to base ten is usually called the decimal logarithm and is simply denoted by lg(x).

It is clear from the recording that the basics are not written in the recording. For example

A natural logarithm is a logarithm whose base is an exponent (denoted by ln(x)).

The exponent is 2.718281828…. To remember the exponent, you can study the rule: the exponent is equal to 2.7 and twice the year of birth of Leo Nikolaevich Tolstoy. Knowing this rule, you will know both the exact value of the exponent and the date of birth of Leo Tolstoy.

And another important logarithm to base two is denoted by

The derivative of the logarithm of a function is equal to one divided by the variable

The integral or antiderivative logarithm is determined by the relationship

The given material is enough for you to solve a wide class of problems related to logarithms and logarithms. To help you understand the material, I will give only a few common examples from the school curriculum and universities.

Examples for logarithms

Logarithm expressions

Example 1.
A). x=10ac^2 (a>0,c>0).

Using properties 3.5 we calculate

2.
By the property of difference of logarithms we have

3.
Using properties 3.5 we find

4. Where .

A seemingly complex expression is simplified to form using a number of rules

Finding logarithm values

Example 2. Find x if

Solution. For calculation, we apply to the last term 5 and 13 properties

We put it on record and mourn

Since the bases are equal, we equate the expressions

Logarithms. First level.

Let the value of logarithms be given

Calculate log(x) if

Solution: Let's take a logarithm of the variable to write the logarithm through the sum of its terms

This is just the beginning of our acquaintance with logarithms and their properties. Practice calculations, enrich your practical skills - you will soon need the knowledge you gain to solve logarithmic equations. Having studied the basic methods for solving such equations, we will expand your knowledge to another equally important topic - logarithmic inequalities...

Basic properties of logarithms

Logarithms, like any numbers, can be added, subtracted and transformed in every way. But since logarithms are not exactly ordinary numbers, there are rules here, which are called main properties.

Adding and subtracting logarithms

Consider two logarithms with the same bases: logax and logay. Then they can be added and subtracted, and:

logax + logay = loga(x y);
logax − logay = loga (x: y).

These formulas will help you calculate a logarithmic expression even when its individual parts are not considered (see the lesson “What is a logarithm”). Take a look at the examples and see:

Task. Find the value of the expression: log6 4 + log6 9.

Since logarithms have the same bases, we use the sum formula:
log6 4 + log6 9 = log6 (4 9) = log6 36 = 2.

Task. Find the value of the expression: log2 48 − log2 3.

The bases are the same, we use the difference formula:
log2 48 − log2 3 = log2 (48: 3) = log2 16 = 4.

Task. Find the value of the expression: log3 135 − log3 5.

Again the bases are the same, so we have:
log3 135 − log3 5 = log3 (135: 5) = log3 27 = 3.

Extracting the exponent from the logarithm

Now let's complicate the task a little. What if the base or argument of a logarithm is a power? Then the exponent of this degree can be taken out of the sign of the logarithm according to the following rules:

It is easy to see that the last rule follows the first two. But it’s better to remember it anyway - in some cases it will significantly reduce the amount of calculations.

How to solve logarithms

This is what is most often required.

Task. Find the value of the expression: log7 496.

Let's get rid of the degree in the argument using the first formula:
log7 496 = 6 log7 49 = 6 2 = 12

Task. Find the meaning of the expression:

Note that the denominator contains a logarithm, the base and argument of which are exact powers: 16 = 24; 49 = 72. We have:

I think the last example requires some clarification. Where have logarithms gone? Until the very last moment we work only with the denominator. We presented the base and argument of the logarithm standing there in the form of powers and took out the exponents - we got a “three-story” fraction.

Transition to a new foundation

Formulas for transition to a new foundation come to the rescue. Let us formulate them in the form of a theorem:

Let the logarithm logax be given. Then for any number c such that c > 0 and c ≠ 1, the equality is true:

In particular, if we set c = x, we get:

These formulas are rarely found in ordinary numerical expressions. It is possible to evaluate how convenient they are only when solving logarithmic equations and inequalities.

However, there are problems that cannot be solved at all except by moving to a new foundation. Let's look at a couple of these:

Task. Find the value of the expression: log5 16 log2 25.

Note that the arguments of both logarithms contain exact powers. Let's take out the indicators: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;

Now let’s “reverse” the second logarithm:

Since the product does not change when rearranging factors, we calmly multiplied four and two, and then dealt with logarithms.

Task. Find the value of the expression: log9 100 lg 3.

The base and argument of the first logarithm are exact powers. Let's write this down and get rid of the indicators:

Now let's get rid of the decimal logarithm by moving to a new base:

Basic logarithmic identity

Often in the solution process it is necessary to represent a number as a logarithm to a given base. In this case, the following formulas will help us:

In the first case, the number n becomes the exponent in the argument. The number n can be absolutely anything, because it is just a logarithm value.

The second formula is actually a paraphrased definition. That's what it's called: .

Like formulas for moving to a new base, the basic logarithmic identity is sometimes the only possible solution.

Task. Find the meaning of the expression:

Note that log25 64 = log5 8 - simply took the square from the base and argument of the logarithm. Taking into account the rules for multiplying powers with the same base, we get:

If anyone doesn’t know, this was a real task from the Unified State Exam :)

Logarithmic unit and logarithmic zero

logaa = 1 is. Remember once and for all: the logarithm to any base a of that base itself is equal to one.
loga 1 = 0 is. The base a can be anything, but if the argument contains one, the logarithm is equal to zero! Because a0 = 1 is a direct consequence of the definition.

That's all the properties. Be sure to practice putting them into practice! Download the cheat sheet at the beginning of the lesson, print it out, and solve the problems.

Maintaining your privacy is important to us. For this reason, we have developed a Privacy Policy that describes how we use and store your information. Please review our privacy practices and let us know if you have any questions.

Collection and use of personal information

Personal information refers to data that can be used to identify or contact a specific person.

You may be asked to provide your personal information at any time when you contact us.

Below are some examples of the types of personal information we may collect and how we may use such information.

What personal information do we collect:

When you submit an application on the site, we may collect various information, including your name, telephone number, email address, etc.

How we use your personal information:

The personal information we collect allows us to contact you with unique offers, promotions and other events and upcoming events.
From time to time, we may use your personal information to send important notices and communications.
We may also use personal information for internal purposes, such as conducting audits, data analysis and various research in order to improve the services we provide and provide you with recommendations regarding our services.
If you participate in a prize draw, contest or similar promotion, we may use the information you provide to administer such programs.

Disclosure of information to third parties

We do not disclose the information received from you to third parties.

Exceptions:

If necessary - in accordance with the law, judicial procedure, in legal proceedings, and/or on the basis of public requests or requests from government authorities in the territory of the Russian Federation - to disclose your personal information. We may also disclose information about you if we determine that such disclosure is necessary or appropriate for security, law enforcement, or other public importance purposes.
In the event of a reorganization, merger, or sale, we may transfer the personal information we collect to the applicable successor third party.

Protection of personal information

We take precautions - including administrative, technical and physical - to protect your personal information from loss, theft, and misuse, as well as unauthorized access, disclosure, alteration and destruction.

Respecting your privacy at the company level

To ensure that your personal information is secure, we communicate privacy and security standards to our employees and strictly enforce privacy practices.

Logarithm positive number N to base(b> 0, b 1 ) called exponent x , to which you need to build b to get N .

Logarithm notation:

This entry is equivalent to the following:b x = N .

EXAMPLES: log 3 81 = 4, since 3 4 = 81;

Log 1/3 27 = – 3, since (1/3) - 3 = 3 3 = 27.

The above definition of logarithm can be written as an identity:

Basic properties of logarithms.

1) log b= 1 , because b 1 = b.

2) log 1 = 0 , because b 0 = 1 .

3) The logarithm of the product is equal to the sum of the logarithms of the factors:

log( ab) = log a+ log b.

4) The logarithm of the quotient is equal to the difference between the logarithms of the dividend and the divisor:

log( a/b) = log a–log b.

5) The logarithm of a power is equal to the product of the exponent and the logarithm of its base:

log (b k ) = k log b.

The consequence of this property is the following:logarithm of the root equal to the logarithm of the radical number divided by the power of the root:

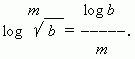
6) If the base of the logarithm is a degree, then the value the inverse of the exponent, can be taken out of the log sign rhyme:

The last two properties can be combined into one:

7) Transition modulus formula (ie. e . transition from one baselogarithm to another base):

In the special case when N=a we have:

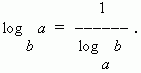
Decimal logarithm called base logarithm 10. It is designated lg, i.e. log 10 N = lg N. Logarithms of numbers 10, 100, 1000, ... p the numbers are 1, 2, 3, …, respectivelythose. have so many positive

units, how many zeros are there in a logarithmic number after one. Logarithms of numbers 0.1, 0.01, 0.001, ... p avna respectively –1, –2, –3, …, i.e. have as many negative ones as there are zeros before one in the logarithmic number ( counting and zero integers). Logarithms other numbers have a fractional part called mantissa. Wholepart of the logarithm is called characteristic. For practical useDecimal logarithms are most convenient.

Natural logarithm called base logarithm e. It is designated ln, i.e. log eN = ln N. Number eis irrational, itapproximate value 2.718281828. It is the limit to which the number tends(1 + 1 / n) n with unlimited increasen(cm. first wonderful limit ).
Strange as it may seem, natural logarithms turned out to be very convenient when carrying out various types of operations related to the analysis of functions.Calculating logarithms to baseecarried out much faster than for any other reason.